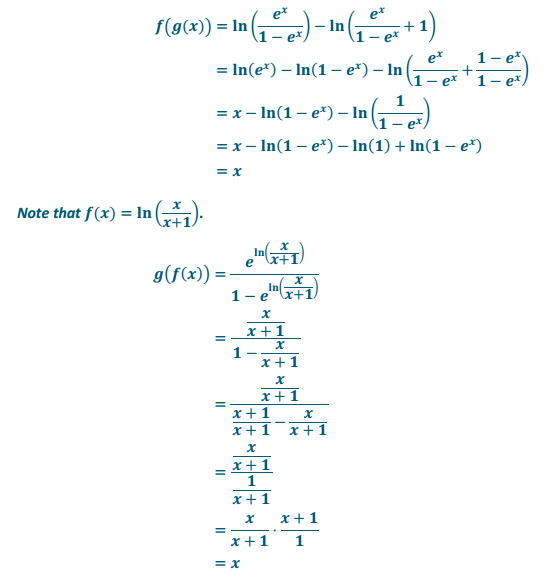Engage NY Eureka Math Precalculus Module 3 Lesson 20 Answer Key
Eureka Math Precalculus Module 3 Lesson 20 Example Answer Key
Example
Given f(x) = 2x, use the definition of the inverse of a function and the definition of a logarithm to write a formula for f-1(x).
y = 2x
If g is the inverse of f, then y = f(x) implies that g(y) = x, so you exchange the x and y variables.
x = 2y
We use this definition of logarithm to rewrite x = 2y to be
log2(x) = y
y = log2(x)
f-1(x) = log2(x)
Eureka Math Precalculus Module 3 Lesson 20 Exercise Answer Key
Opening Exercise
Let f(x) = 2x.
a. Complete the table, and use the points (x,f(x)) to create a sketch of the graph of y = f(x).
Answer:
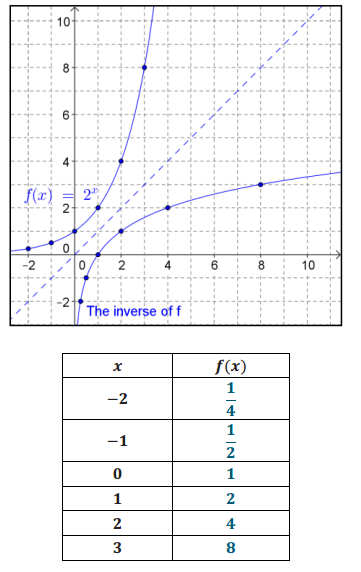
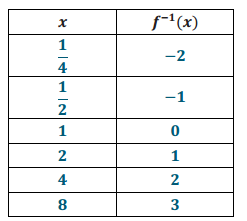
b. Create a table of values for the function f-1, and sketch the graph of y = f-1 (x) on the grid above.
Answer:
The inverse is sketched above.
c. What type of function is f-1? Explain how you know.
Answer:
It appears to be a logarithmic function. We are plotting powers of 2 on the horizontal axis and the corresponding exponents on the vertical axis. This is how we define a logarithmic function.
Exercises
Exercise 1.
Find the value of y in each equation. Explain how you determined the value of y.
a. y = log2(22)
Answer:
y = 2 because the logarithm of 22 is the exponent to which you would raise 2 to get 22.
b. y = log2(25)
Answer:
y = 5 because the logarithm of 25 is the exponent to which you would raise 2 to get 25.
c. y = log2(2-1)
Answer:
y = – 1 because the logarithm of 2-1 is the exponent to which you would raise 2 to get 2-1.
d. y = log2(2x)
Answer:
y = x because the logarithm of 2x is the exponent to which you would raise 2 to get 2x.
Exercise 2.
Let f(x) = log2(x) and g(x) = 2x.
a. What is f(g(x))?
Answer:
f(g(x)) = log2(2x )
Thus, f(g(x)) = x.
b. Based on the results of part (a), what can you conclude about the functions f and g?
Answer:
The two functions would be inverses.
Exercise 3.
Find the value of y in each equation. Explain how you determined the value of y.
a. y = 3log3(3)
Answer:
y = 3 because log3(3) = 1, and by substituting, we get y = 31 = 3.
b. y = 3log3(9)
Answer:
y = 9 because log3(9) = 2, and by substituting, we get y = 32 = 9.
c. y = 3log3(81)
Answer:
y = 81 because log3(81) = 4, and by substituting, we get y = 34 = 81.
d. y = 3log3(x)
Answer:
y = x because if we rewrite the equation in logarithm form, we get log3(y) = log3(x), which shows that y = x.
Exercise 4.
Let f(x) = log3(x) and g(x) = 3x.
a. What is g(f(x))?
Answer:
g(f(x)) = 3log3(x)
Thus, g(f(x)) = x.
b. Based on the results in part (a), what can you conclude about the functions f and g?
Answer:
The functions f and g are inverses.
Exercise 5.
Verify by composition that the functions f(x) = bx and g(x) = logb(x) for b>0 are inverses of one another.
We need to show that f(g(x)) = blogb(x) = x.
Let y = blogb(x).
Then, using the definition of logarithm,
logb(y) = logb(x),
which means that y = x. Substituting into the equation above,
x = blogb(x).
We also need to show that g(f(x)) = logb(bx) = x.
Let y = logb(bx).
Then, using the definition of logarithm,
by = bx,
which means that y = x. Substituting into the equation above,
x = logb(bx).
Exercise 6.
The graph of y = f(x), a logarithmic function, is shown below.
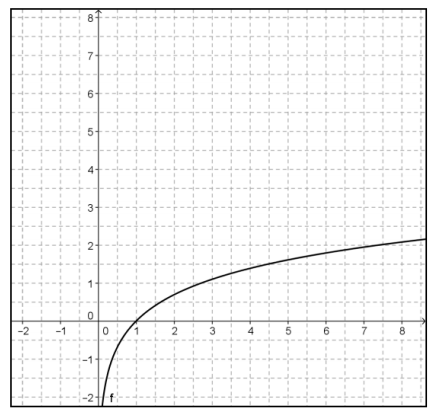
a. Construct the graph of y = f-1(x).
Answer:
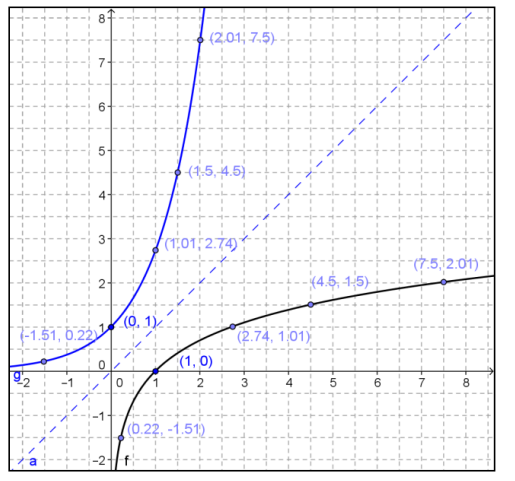
b. Estimate the base b of these functions. Explain how you got your answer.
Answer:
f(b) = 1 gives a value for b≈2.75. Thus, the base appears to be about 2.75 because logbb = 1 for any base b. You can see on the exponential graph that x is 1, and the corresponding y – value is 2.75.
Exercise 7.
Use a calculator to get a very accurate estimate of the irrational number e.
Answer:
On the calculator, e≈2.718 281 828 46.
Exercise 8.
Is the graph of y = f-1(x) in Exercise 6 a good approximation of the function g(x) = ex? Explain your reasoning.
Answer:
We estimated that the base was 2.75, so it is close to the value of e.
Exercise 9.
Show that f(x) = ln(x) and g(x) = ex are inverse functions by graphing y = f(g(x)) and y = g(f(x)) on a graphing calculator. Explain how your graphs support the fact that these two functions are indeed inverses of one another.
Answer:
When graphed, the graphs of y = f(g(x)) and y = g(f(x)) are the same as the graph of y = x for all values of x.
Exercise 10.
What is the base of the natural logarithm function f(x) = ln(x)? Explain how you know.
Answer:
Based on the results of Exercise 9, we can conclude that the base of the natural logarithm function is the irrational number e.
Exercise 11.
Find the inverse of each function.
a. f(x) = 2x – 3
Answer:
y = 2x – 3
x = 2y – 3
log2(x) = y – 3
y = 3 + log2(x)
f-1(x) = 3 + log2(x)
b. g(x) = 2 log(x – 1)
Answer:
y = 2 log(x – 1)
x = 2 log(y – 1)
\(\frac{x}{2}\) = log(y – 1)
\(10^{\frac{x}{2}}\) = y – 1
y = \(10^{\frac{x}{2}}\) + 1
g-1(x) = \(10^{\frac{x}{2}}\) + 1
c. h(x) = ln(x) – ln(x – 1)
Answer:
y = ln(x) – ln(x – 1)
x = ln(y) – ln(y – 1)
x = \(\ln \left(\frac{y}{y – 1}\right)\)
ex = \(\frac{y}{y – 1}\)
ex (y – 1) = y
ex y – y = ex
y(ex – 1) = ex
y = \(\frac{e^{x}}{e^{x} – 1}\)
h-1(x) = \(\frac{e^{x}}{e^{x} – 1}\)
d. k(x) = \(5 – 3^{ – \frac{x}{2}}\)
Answer:
y = \(5 – 3^{ – \frac{x}{2}}\)
x = \(5 – 3^{ – \frac{y}{2}}\)
5 – x = \(3^{ – \frac{y}{2}}\)
log3(5 – x) = – \(\frac{y}{2}\)
– 2 log3(5 – x) = y
k-1(x) = – 2 log3(5 – x)
Exercise 12.
Check your solutions to Exercise 11 by graphing the functions and the inverses that you found and verifying visually that the reflection property holds.
Answer:
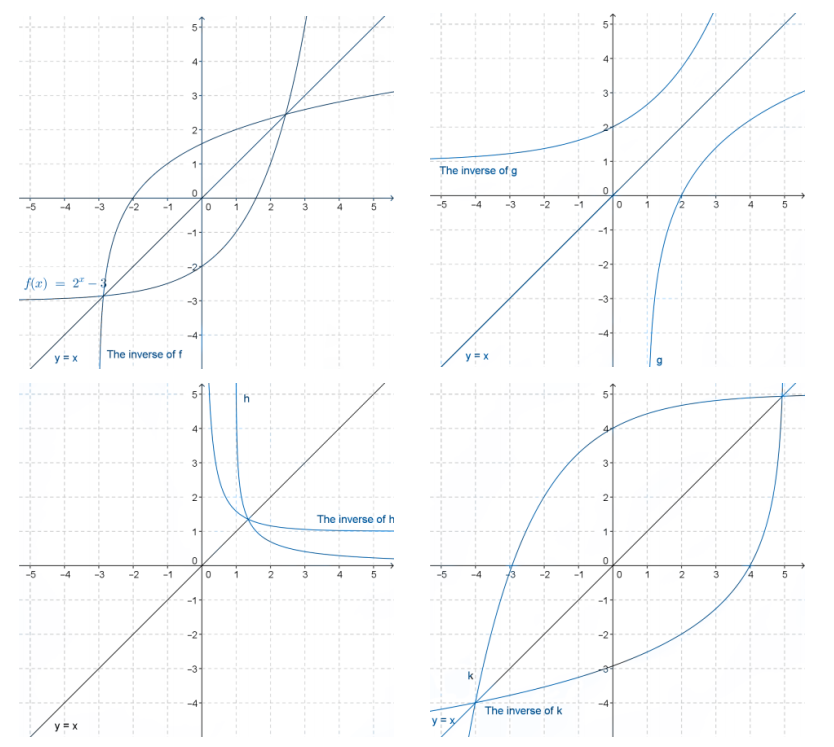
Eureka Math Precalculus Module 3 Lesson 20 Problem Set Answer Key
Question 1.
Find the inverse of each function.
a. f(x) = 3x
Answer:
f-1(x) = log3(x)
b. f(x) = (1/2)x
Answer:
f-1(x) = log0.5(x)
Or students may rewrite this as f(x) = 2 – x and then exchange x and y and solve for y getting
f-1(x) = – log2(x).
c. g(x) = ln(x – 7)
Answer:
g-1(x) = ex + 7
d. h(x) = \(\frac{\log _{3}(x + 2)}{\log _{3}(5)}\)
Answer:
By rewriting using the change of base property, h(x) = log5(x + 2), so
h-1(x) = 5x – 2.
e. f(x) = 3(1.8)0.2x + 3
Answer:
f-1(x) = 5 log(1.8)\(\left(\frac{x – 3}{3}\right)\)
f. g(x) = \(\log _{2}(\sqrt[3]{x – 4})\)
Answer:
g-1(x) = (2 – x)3 + 4
= 23x + 4
g. h(x) = \(\frac{5^{x}}{5^{x} + 1}\)
Answer:
x(5y + 1) = 5y
x⋅5y + x = 5y
x⋅5y – 5y = – x
5y (x – 1) = – x
5y = – \(\frac{x}{x – 1}\)
h-1(x) = \(\log _{5}\left( – \frac{x}{x – 1}\right)\)
h. f(x) = 2 – x + 1
Answer:
f-1(x) = – log2(x) + 1
i. g(x) = \(\sqrt{\ln (3 x)}\)
Answer:
g-1(x) = \(\frac{1}{3} e^{\left(x^{2}\right)}\)
j. h(x) = \(e^{\frac{1}{5} x + 3} – 4\)
Answer:
h-1(x) = 5 ln(x + 4) – 15
Question 2.
Consider the composite function f∘g, composed of invertible functions f and g.
a. Either f-1 ∘ g-1or g-1 ∘ f-1is the inverse of the composite function. Which one is it? Explain.
Answer:
g-1 ∘ f-1is the inverse of the composite function. In this order, the g and g-1match up, or the f and f-1match up.
b. Show via composition of functions that your choice of (f ∘ g)-1 was the correct choice. (Hint: Function composition is associative.)
Answer:
(g-1 ∘ f-1 ) ∘ (f ∘ g) = g-1∘(f-1 ∘ f) ∘ g
= g-1 ∘ g
(f ∘ g) ∘ (g-1 ∘ f-1 ) = f ∘ (g ∘ g-1 ) ∘ f-1
= f ∘ f-1
Each time we were able to group the base functions and their inverses together, the result is the identity function. Alternatively, we could have applied the functions to a point x and used the same argument to have a final result of x.
Question 3.
Let m(x) = \(\frac{x}{ x – 1}\).
a. Find the inverse of m.
Answer:
x = \(\frac{y}{y – 1}\)
x(y – 1) = y
xy – x = y
xy – y = x
y(x – 1) = x
y = \(\frac{x}{x – 1}\)
The function is its own inverse.
b. Graph m. How does the graph of m explain why this function is its own inverse?
Answer:
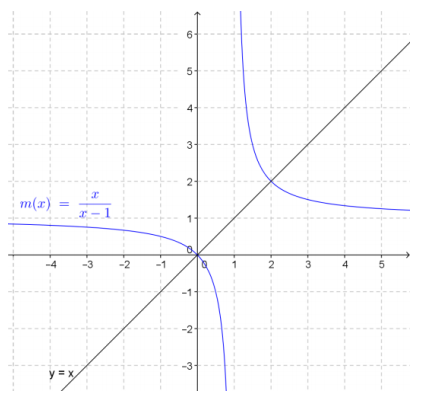
Each point on the graph of m reflects to another point on the graph of m when reflected about the line y = x.
c. Think of another function that is its own inverse.
Answer:
f(x) = \(\frac{1}{x}\) has this same reflective property.
Extension:
Question 4.
One of the definitions of e involves the infinite series \(1 + 1 + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \cdots + \frac{1}{n !} + \cdots\) A generalization exists to define e – x:
\(e^{x} = 1 + x + \frac{x^{2}}{2} + \frac{x^{3}}{6} + \frac{x^{4}}{24} + \cdots + \frac{x^{n}}{n !} + \cdots\)
This series definition of e – x allows us to approximate powers of the transcendental number e using strictly rational numbers. This definition is accurate for all real numbers.
a. Verify that the formula given for e can be obtained by substituting 1 for x into the formula for e – x.
Answer:
\(e^{1} = 1 + (1) + \frac{(1)^{2}}{2} + \frac{(1)^{3}}{6} + \frac{(1)^{4}}{24} + \cdots + \frac{(1)^{n}}{n !} + \cdots\)
b. Use the first seven terms of the series to calculate e, e2, and e3.
Answer:
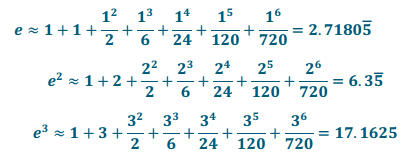
c. Use the inverse of y = e – x to see how accurate your answer to part (b) is.
Answer:
\(\ln (6.3 \overline{5})\)≈1.849
ln(17.1625) ≈ 2.843
d. Newer calculators and computers use these types of series carried out to as many terms as needed to produce their results for operations that are not otherwise obvious. It may seem cumbersome to calculate these by hand knowing that computers can calculate hundreds and thousands of terms of these series in a single second. Use a calculator or computer to compare how accurate your results from part (b) were to the value given by your technology.
Answer:
e2 ≈ 7.389
e3 ≈ 20.086
We were off by about 1 \(\frac{1}{2}\) and by about 3.
e. \(\ln \left(\frac{x}{x – 1}\right) = \frac{1}{x} + \frac{1}{2 x^{2}} + \frac{1}{3 x^{3}} + \frac{1}{4 x^{4}} + \cdots + \frac{1}{n x^{n}}\) + ⋯ for |x| > 1. What does your response to Exercise 3
part (a) tell you that ln(x) is equal to?
Answer:
Since y = \(\frac{x}{x + 1}\) is its own inverse, you can compose it inside the logarithm to get ln(x). That means substituting the expression \(\frac{x}{x + 1}\) for each x in both sides of the equation results in
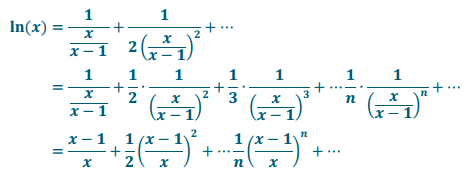
Eureka Math Precalculus Module 3 Lesson 20 Exit Ticket Answer Key
Question 1.
Find the inverse of each function.
a. f(x) = log2(x) + 2
Answer:
f-1(x) = 2x – 2
b. g(x) = ex – 4
Answer:
g-1(x) = ln(x) + 4
c. h(x) = 3 log(2 + 3x)
Answer:
h-1(x) = \(\frac{1}{3}\left(10^{\frac{x}{3}} – 2\right)\)
Question 2.
Verify by composition that the given functions are inverses.
a. f(x) = 2 – log(3x + 2); g(x) = \(\frac{1}{3}\)(100⋅10 – x – 2)
Answer:
f(g(x)) = f(\(\frac{1}{3}\) (100⋅10 – x – 2))
= 2 – log(3(\(\frac{1}{3}\) (100⋅10 – x – 2)) + 2)
= 2 – log(100⋅10 – x – 2 + 2)
= 2 – log(102 – x)
= 2 – (2 – x)
= x
g(f(x)) = \(\frac{1}{3}\left(100 \cdot 10^{ – (2 – \log (3 x + 2))} – 2\right)\)
= \(\frac{1}{3}\left(100 \cdot \frac{3 x + 2}{100} – 2\right)\)
= \(\frac{1}{3}\) (3x + 2 – 2)
= \(\frac{1}{3}\) (3x)
= x
b. f(x) = ln(x) – ln(x + 1); g(x) = \(\frac{e^{x}}{1 – e^{x}}\)
Answer: