Engage NY Eureka Math Precalculus Module 3 Lesson 15 Answer Key
Eureka Math Precalculus Module 3 Lesson 15 Example Answer Key
Example 1.
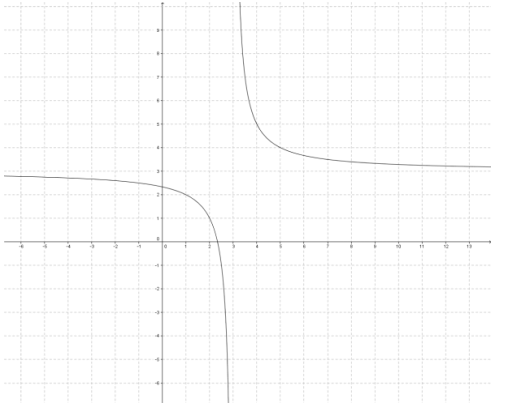
Graph the function f(x) = \(\frac{x + 2}{x – 3}\) using transformations of the graph of y = \(\frac{1}{x}\).
Answer:
f(x) = \(\frac{x – 3 + 5}{x – 3}\) = 1 + \(\frac{5}{x – 3}\)
Eureka Math Precalculus Module 3 Lesson 15 Exploratory Challenge/Exercise Answer Key
Exploratory Challenge/Exercises 1–2
Exercise 1.
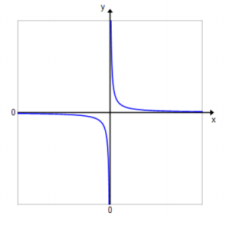
Sketch the general shape of the graph of the function f(x) = \(\frac{1}{x^{n}}\) for n > 0 when n is an odd number.
Answer:
Exercise 2.
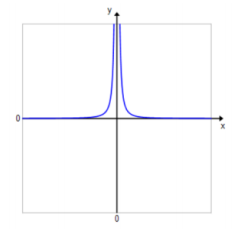
Sketch the general shape of the graph of the function f(x) = \(\frac{1}{x^{n}}\) for n>0 when n is an even number.
Answer:
Exercises 3–5
Exercise 3.
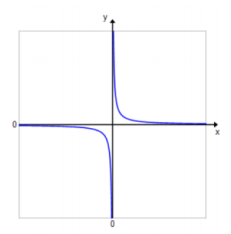
Sketch the graph of the function f(x) = \(\frac{1}{x}\). Then, use the graph of f to sketch each transformation of f showing the vertical and horizontal asymptotes.
Answer:
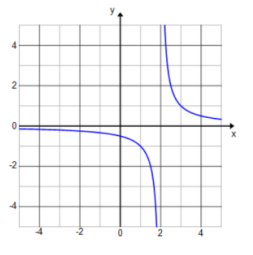
a. g(x) = \(\frac{1}{x – 2}\)
Answer:
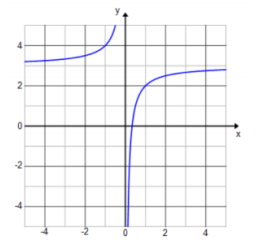
b. h(x) = – \(\frac{1}{x}\) + 3
Answer:
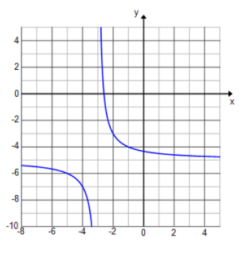
c. k(x) = \(\frac{2}{x + 3}\) – 5
Answer:
Exercise 4.
Use your results from Exercise 3 to make some general statements about graphs of functions in the form f(x) = a + \(\frac{b}{x – c}\). Describe the effect that changing each parameter a,b,and c has on the graph of f.
Answer:
a represents the vertical shift. A positive value of a shifts the graph up a units, and a negative value shifts the graph down a units. The horizontal asymptote is y = a. c represents the horizontal shift. A positive value of c shifts the graph right c units, and a negative value shifts the graph left c units. The vertical asymptote is x = c. b represents the vertical scaling. For values of b such that |b| > 1, the graph stretches vertically. For values of b such that 0 < |b| < 1, the graph compresses vertically. When b is negative, the graph reflects across the x – axis.
Exercise 5.
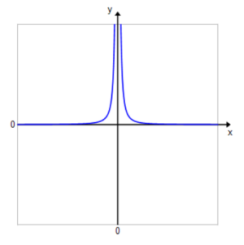
Sketch the graph of the function f(x) = \(\frac{1}{x^{2}}\). Then, use the graph of f to sketch each transformation of f showing the vertical and horizontal asymptotes.
Answer:
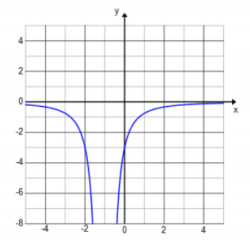
a. g(x) = – \(\frac{3}{(x + 1)^{2}}\)
Answer:
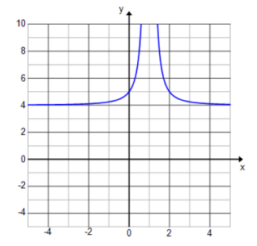
b. h(x) = \(\frac{1}{(x – 1)^{2}}\) + 4
Answer:
Exercises 6–13
Sketch each function by using transformations of the graph of y = \(\frac{1}{x}\) or the graph of y = \(\frac{1}{x^{2}}\). Explain the transformations that are evident in each example.
Exercise 6.
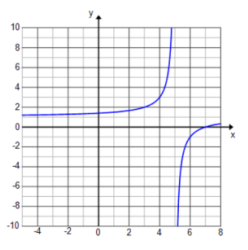
f(x) = \(\frac{x – 7}{x – 5}\)
Answer:
f(x) = 1 – \(\frac{2}{x – 5}\)
The graph is shifted right 5 units.
Exercise 7.
f(x) = \(\frac{2 x + 6}{x + 1}\)
Answer:
f(x) = \(\frac{x + 1 + x + 1 + 4}{x + 1}\) = 1 + 1 + \(\frac{4}{x + 1}\) = 2 + \(\frac{4}{x + 1}\)
The graph is shifted left 1 unit and up 2 units.
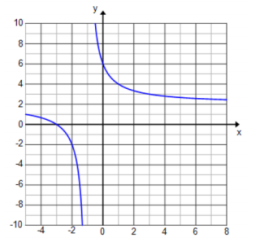
Exercise 8.
f(x) = \(\frac{2 x^{2} – 1}{x^{2}}\)
Answer:
f(x) = 2 – \(\frac{1}{x^{2}}\)
The graph is shifted up 2 units, and both branches are going down.
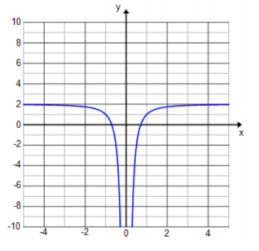
Exercise 9.
f(x) = \(\frac{1 + 4 x^{3}}{x^{3}}\)
Answer:
f(x) = \(\frac{1}{x^{3}}\) + 4
The graph is shifted up 4 units.
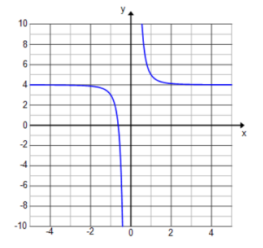
Exercise 10.
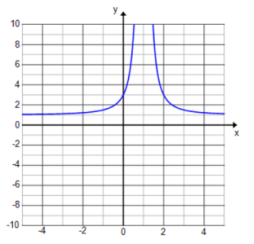
f(x) = \(\frac{x^{2} – 2 x + 3}{(x – 1)^{2}}\)
Answer:
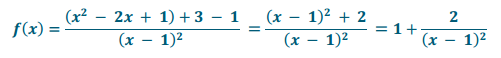
The graph is shifted right 1 unit and up 1 unit. Both branches go up.
Exercise 11.
f(x) = \(\frac{2 x^{2} + 12 x + 13}{(x + 3)^{2}}\)
Answer:
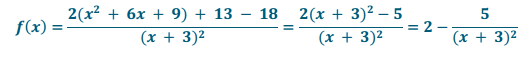
The graph is shifted left 3 units and up 2 units. Both branches go down.
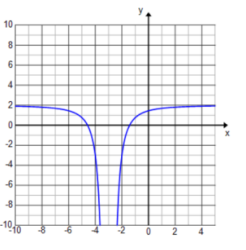
Exercise 12.
f(x) = \(\frac{x + 4}{x^{2} – 16}\)
Answer:
f(x) = \(\frac{1}{x – 4}\), x≠ – 4
The graph is shifted right 4 units, and there is a value missing at x = – 4.
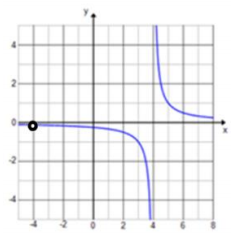
Exercise 13.
f(x) = \(\frac{x}{x^{3} – 4 x^{2} + 4 x}\)
Answer:
f(x) = \(\frac{1}{(x – 2)^{2}}\), x≠0
The graph is shifted right 2 units, and there is a value missing at x = 0.
Both branches go up.
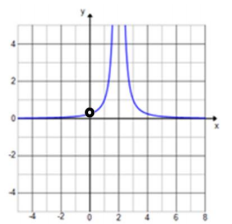
Eureka Math Precalculus Module 3 Lesson 15 Problem Set Answer Key
Question 1.
Write each function so that it appears to be a transformation of y = \(\frac{1}{x^{n}}\). Then, explain how the graph of each function relates to the graph of y = \(\frac{1}{x^{n}}\).
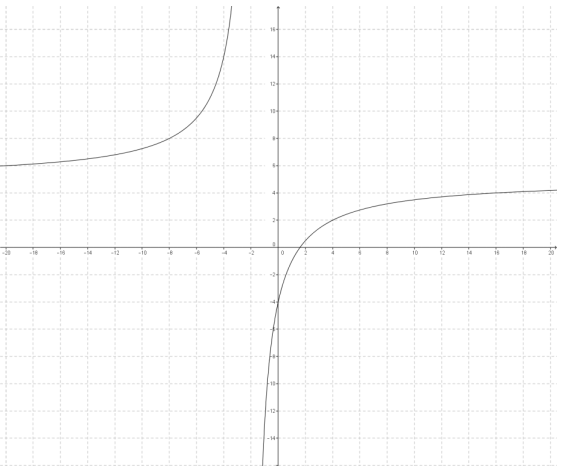
a. y = \(\frac{5 x – 8}{x + 2}\)
Answer:
y = \(\frac{5 x + 10 – 18}{x + 2}\) = 5 – \(\frac{18}{x + 2}\)
The graph would be the graph of y = \(\frac{1}{x}\) shifted left 2 units, stretched vertically by a scale factor of 18, reflected across the x – axis, and shifted up 5 units.
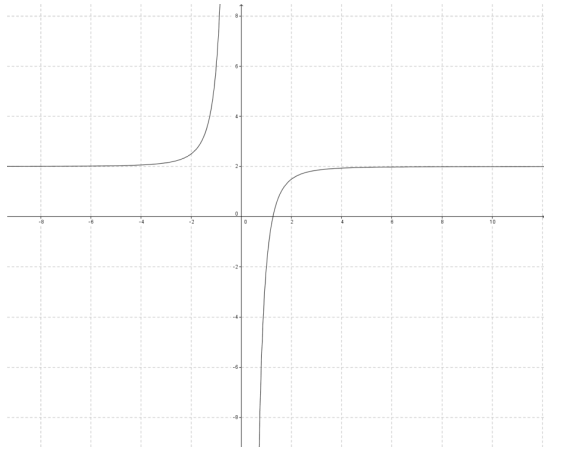
b. y = \(\frac{2 x^{3} – 4}{x^{3}}\)
Answer:
y = 2 – \(\frac{4}{x^{3}}\)
The graph would be the graph of y = \(\frac{1}{x^{3}}\) stretched vertically by a scale factor of 4, reflected across the x – axis, and shifted up 2 units.
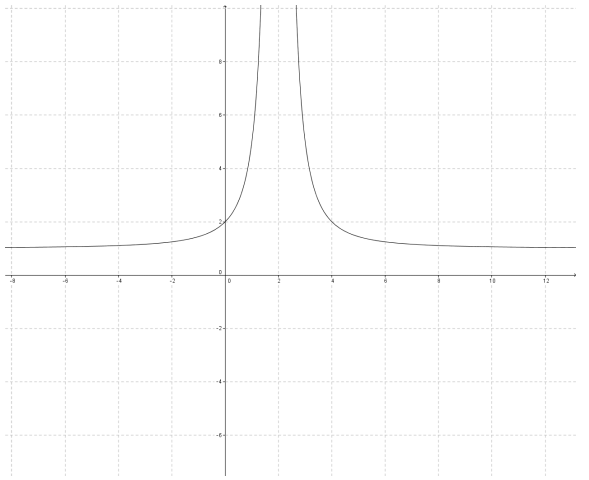
c. y = \(\frac{x^{2} – 4 x + 8}{(x – 2)^{2}}\)
Answer:
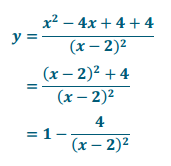
The graph would be the graph of y = \(\frac{1}{x^{2}}\) shifted right 2 units, stretched vertically by a scale factor of 4, reflected across the x – axis, and shifted up 1 unit.
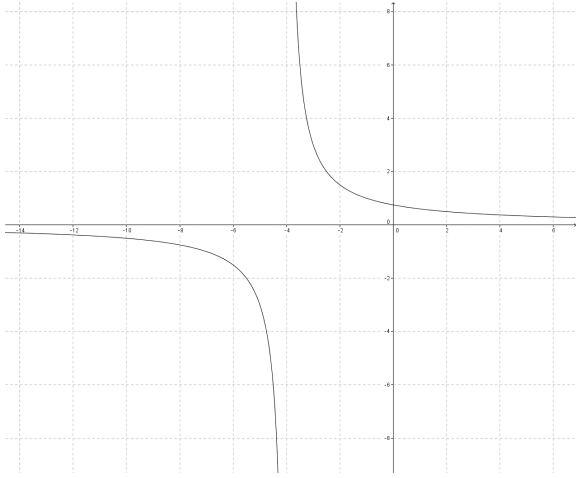
d. y = \(\frac{3 x – 12}{x^{2} – 16}\)
Answer:
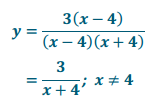
The graph would be the graph of y = \(\frac{1}{x}\) shifted left 4 units and stretched vertically by a scale factor of 3. The point at x = 4 would be missing from the graph.
e. y = \(\frac{2 x^{2} + 16 x + 25}{x^{2} + 8 x + 16}\)
Answer:
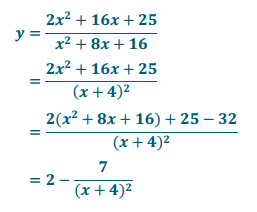
The graph would be the graph of y = \(\frac{1}{x^{2}}\) shifted left 4 units, stretched vertically by a scale factor of 7, reflected across the x – axis, and shifted up 2 units.
Question 2.
For each function in Problem 1, state how the horizontal and vertical asymptotes are affected from the original graph of y = \(\frac{1}{x^{n}}\).
Answer:
a. The horizontal asymptote is moved up 5; the vertical asymptote is moved 2 to the left.
b. The horizontal asymptote is moved up 2; the vertical asymptote is unchanged.
c. The horizontal asymptote is moved up 1; the vertical asymptote is moved to the right 2.
d. The horizontal asymptote is unchanged; the vertical asymptote is moved to the left 4.
e. The horizontal asymptote is moved up 2; the vertical asymptote is moved to the left.
Question 3.
Sketch a picture of the graph of each function in Problem 1.
Answer:
a.
b.
c.
d.
e.
Question 4.
What are some indicators whether or not a rational function can be expressed as a transformation of y = \(\frac{1}{x^{n}}\)?
Answer:
If the variables in the numerator can be expressed as a part of a multiple of the denominator, then the function is able to be expressed as a transformation. If it cannot, then there is a variable term in the numerator that cannot be removed that is the result of a composition or product of functions and not from a transformation.
Question 5.
Write an equation for a function whose graph is a transformation of the graph y = \(\frac{1}{x}\). The graph has been shifted right 2 units, stretched vertically by a factor of 2, and shifted down 3 units.
Answer:
y = \(\frac{2}{x – 2}\) – 3
Eureka Math Precalculus Module 3 Lesson 15 Exit Ticket Answer Key
Question 1.
Sketch the graph of the function given below by using transformations of y = \(\frac{1}{x^{n}}\) . Explain which transformations you used and how you identified them.
Answer:
y = \(\frac{3 x – 7}{x – 3}\)
y = \(\frac{3 x – 9 + 2}{x – 3}\) = 3 + \(\frac{2}{x – 3}\)
By rewriting the function into the form a + \(\frac{b}{x-c}\), I saw that the graph was shifted right 3 units, stretched vertically by a factor of 2, and shifted up 3 units.