Engage NY Eureka Math Precalculus Module 3 Lesson 14 Answer Key
Eureka Math Precalculus Module 3 Lesson 14 Example Answer Key
Example 1.
Sketch the graph of the rational function f(x) = \(\frac{2 x^{2} – x}{x^{2} – 16}\) showing all the key features of the graph. Label the key features on your graph.
Answer:
D: set of all real numbers except x = 4, – 4
Vertical asymptotes: x = 4 and x = – 4
Test values near the vertical asymptotes:
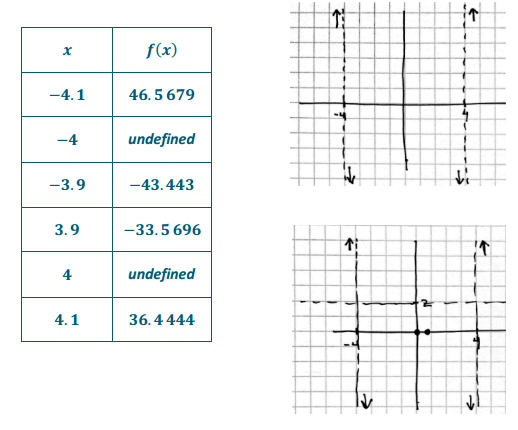
End behavior: As x → ∞, y → 2.
Horizontal asymptote: y = 2
x – intercepts: 2x2 – x = 0 → x = 0, \(\frac{1}{2}\) → (0,0) and (\(\frac{1}{2}\),0)
y – intercept: (0, 0)
Example 2.
Graph the function f(x) = \(\frac{x^{2} + 5 x – 6}{x + 1}\) showing all the key features.
Answer:
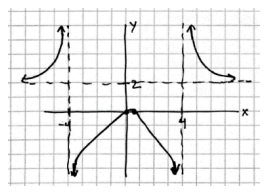
D: set of all real numbers except x = – 1
Vertical asymptote: x = – 1
Test values near the vertical asymptote:
End behavior: As x → ∞, y → ∞. As x → – ∞, y → – ∞.
x – intercepts: x2 + 5x – 6 = 0 → x = – 6, 1 → ( – 6,0)and (1,0)
y – intercept: (0, – 6)
Eureka Math Precalculus Module 3 Lesson 14 Exercise Answer Key
Opening Exercise
State the domain of each of the following functions. Then, determine whether or not the excluded value(s) of x are vertical asymptotes on the graph of the function. Give a reason for your answer.
a. f(x) = \(\frac{x^{2} – 3 x + 2}{x – 2}\)
Answer:
D: the set of all real numbers except x = 2
x = 2 is not a vertical asymptote on the graph of f because as x → 2, f(x) → 1.
b. f(x) = \(\frac{x^{2} + 3 x + 2}{x – 2}\)
Answer:
D: the set of all real numbers except x = 2
x = 2 is a vertical asymptote on the graph of f because as x → 2, f(x) → ∞ on one side and –∞ on one side.
Exercises
Sketch the graph of each rational function showing all the key features. Verify your graph by graphing the function on the graphing calculator.
Exercise 1.
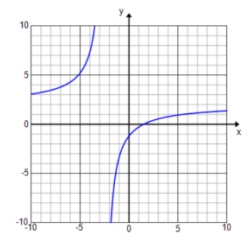
f(x) = \(\frac{4 x – 6}{2 x + 5}\)
Answer:
D: set of all real numbers except x = – \(\frac{5}{2}\)
Vertical asymptotes: x = – \(\frac{5}{2}\)
End behavior: As x → ∞, y → 2.
Horizontal asymptote: y = 2
x – intercept: (\(\frac{3}{2}\), 0)
y – intercept: (0, – \(\frac{6}{5}\))
Exercise 2.
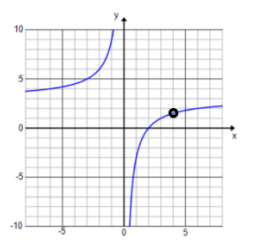
f(x) = \(\frac{(3 x – 6)(x – 4)}{x(x – 4)}\)
Answer:
Equivalent form: f(x) = \(\frac{3 x – 6}{x}\) with x ≠ 4
D: set of all real numbers except x = 0, 4
Vertical asymptotes: x = 0
End behavior: As x → ∞, y → 3.
Horizontal asymptote: y = 3
x – intercept: (2, 0)
y – intercept: none
Exercise 3.
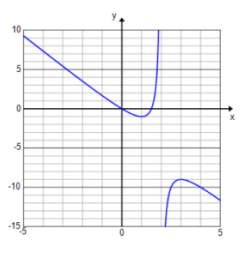
f(x) = \(\frac{3 x – 2 x^{2}}{x – 2}\)
Answer:
D: set of all real numbers except x = 2
Vertical asymptotes: x = 2
End behavior: As x → ∞, y → – ∞. As x → – ∞, y → ∞.
x – intercept: (0, 0) and (\(\frac{3}{2}\), 0)
y – intercept: (0, 0)
Exercise 4.
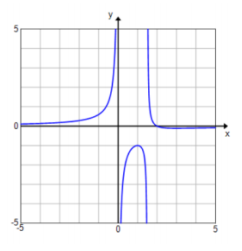
f(x) = \(\frac{x – 2}{3 x – 2 x^{2}}\)
Answer:
D: set of all real numbers except x = 0, \(\frac{3}{2}\)
Vertical asymptotes: x = 0 and x = \(\frac{3}{2}\)
End behavior: As x → ∞,y → 0.
Horizontal asymptote: y = 0
x – intercept: (2, 0)
y – intercept: none
Exercise 5.
f(x) = \(\frac{x}{x^{2} – 9}\)
Answer:
D: set of all real numbers except x = – 3, 3
Vertical asymptotes: x = – 3 and x = 3
End behavior: As x → ∞, y → 0.
Horizontal asymptote: y = 0
x – intercept: (0, 0)
y – intercept: (0, 0)
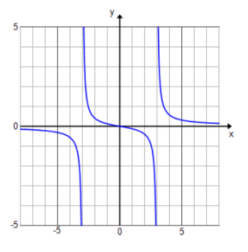
Exercise 6.
f(x) = \(\frac{x^{2}}{x^{2} – 9}\)
Answer:
D: set of all real numbers except x = – 3, 3
Vertical asymptotes: x = – 3 and x = 3
End behavior: As x → ∞, y → 1.
Horizontal asymptote: y = 1
x – intercept: (0, 0)
y – intercept: (0, 0)
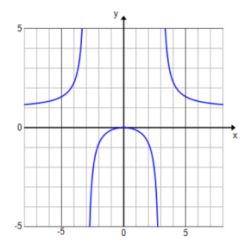
Exercise 7.
f(x) = \(\frac{x^{2} – 9}{x}\)
Answer:
D: set of all real numbers except x = 0
Vertical asymptotes: x = 0
End behavior: As x → ∞, y → ∞. As x → – ∞, y → – ∞.
x – intercept: ( – 3, 0) and (3, 0)
y – intercept: none
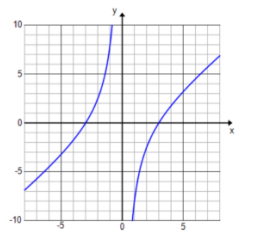
Exercise 8.
f(x) = \(\frac{x^{2} – 9 x}{x}\)
Answer:
D: set of all real numbers except x = 0
Equivalent function: f(x) = x – 9, x ≠ 0
End behavior: As x → ∞, y → ∞. As x → – ∞, y → – ∞.
x – intercept: (9, 0)
y – intercept: none
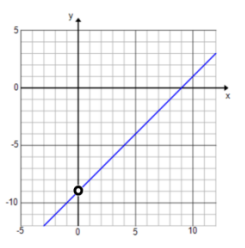
Exercise 9.
f(x) = \(\frac{x^{3} – 8}{x – 2}\)
Answer:
D: set of all real numbers except x = 2
Equivalent function: f(x) = x2 + 2x + 4, x ≠ 2
End behavior: As x → ∞, y → ∞. As x → – ∞, y → ∞.
x – intercept: none
y – intercept: (0, 4)
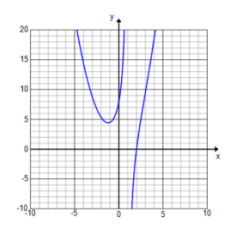
Exercise 10.
f(x) = \(\frac{x^{3} – 8}{x – 1}\)
Answer:
D: set of all real numbers except x = 1
Vertical asymptote: x = 1
End behavior: As x → ∞, y → ∞. As x → – ∞, y → – ∞.
x – intercept: (2, 0)
y – intercept: (0, 8)
Eureka Math Precalculus Module 3 Lesson 14 Problem Set Answer Key
Question 1.
List all of the key features of each rational function and its graph, and then sketch the graph showing the key features.
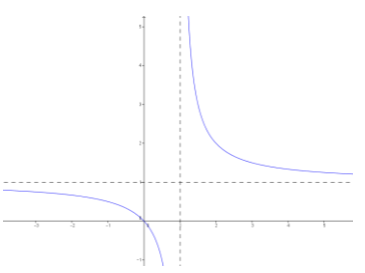
a. y = \(\frac{x}{x – 1}\)
Answer:
D: set of all real numbers except x = 1
Vertical asymptote: x = 1
End behavior: As x → ∞, y → 1.
Horizontal asymptote: y = 1
x – intercept: (0, 0)
y – intercept: (0, 0)
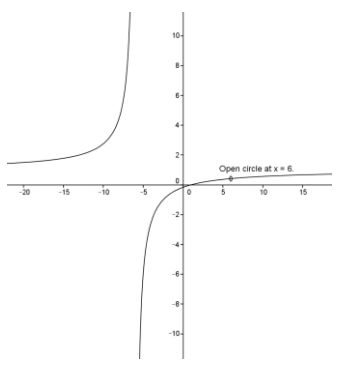
b. y = \(\frac{x^{2} – 7 x + 6}{x^{2} – 36}\)
D: set of all real numbers except x = 6 and x = – 6
Equivalent function: f(x) = \(\frac{x – 1}{x + 6}\) with x ≠ 6
Vertical asymptote: x = – 6
End behavior: As x → ∞, y → 1.
Horizontal asymptote: y = 1
x – intercept: (0, 0)
y – intercept: (0, 0)
c. y = \(\frac{x^{3} – 3 x^{2} – 10 x}{x^{2} + 8 x – 65}\)
D: set of all real numbers except x = – 13 and x = 5
Equivalent function: f(x) = \(\frac{x(x + 2)}{x + 13}\) with x ≠ 5
Vertical asymptote: x = – 13
End behavior: As x → ∞, y → ∞.
Horizontal asymptote: None—there is a slant asymptote.
x – intercepts: (0, 0), ( – 2, 0)
y – intercept: (0, 0)
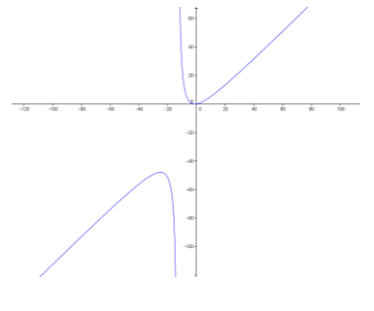
Question 2.
y = \(\frac{3 x}{x^{2} – 1}\)
Answer:
D: set of all real numbers except x = – 1 and x = 1
Vertical asymptotes: x = – 1 and x = 1
End behavior: As x → ∞, y → 0.
Horizontal asymptote: y = 0
x – intercept: (0, 0)
y – intercept: (0, 0)
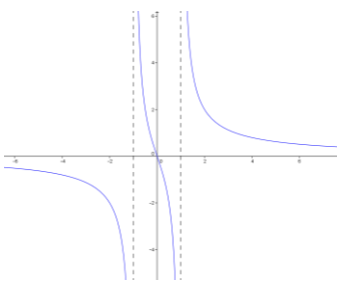
Question 3.
Graph y = \(\frac{1}{x^{2}}\) and y = \(\frac{1}{x}\). Compare and contrast the two graphs.
Answer:
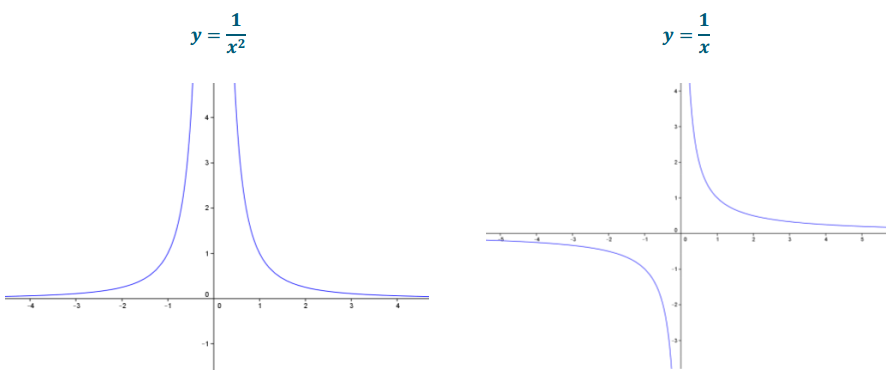
Neither graph has any intercepts. The graphs have the same vertical asymptote (x = 0) and horizontal asymptote (y = 0). The difference is that the graph of y = \(\frac{1}{x^{2}}\) is always positive while the graph of y = \(\frac{1}{x}\) is negative for x – values less than 0.
Extension:
Question 3.
Consider the function f(x) = \(\frac{x^{3} + 1}{x}\)
a. Use the distributive property to rewrite f as the sum of two rational functions g and h.
Answer:
f(x) = x2 + \(\frac{1}{x}\); g(x) = x2 ; h(x) = \(\frac{1}{x}\)
b. What is the end behavior of g? What is the end behavior of h?
Answer:
As x → ±∞, g(x) → ∞. As x → ±∞, h(x) → 0.
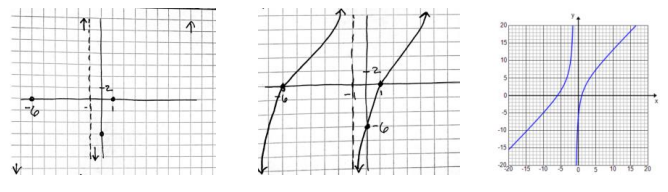
c. Graph y = f(x) and y = x2 on the same set of axes. What do you notice?
Answer:
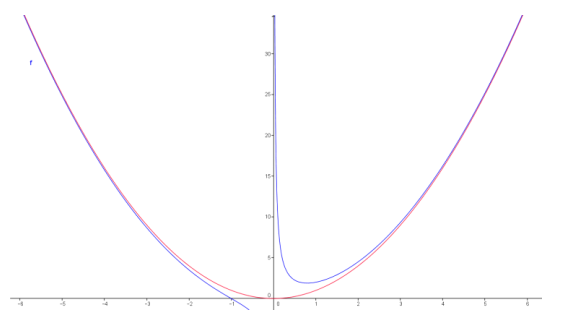
d. Summarize what you have discovered in parts (b) and (c).
Answer:
As x increases without bound, the graph of f approaches the graph of g, and similarly, as x decreases without bound.
Question 4.
Number theory is a branch of mathematics devoted primarily to the study of integers. Some discoveries in number theory involve numbers that are impossibly large such as Skewes’ numbers and Graham’s number. One Skewes’ number is approximately e((e((e79)))), and Graham’s number is so large that to even write it requires 64 lines of writing with a new operation (one that can be thought of as the shortcut for repeated exponentiation). In fact, both of these numbers are so large that the decimal representation of the numbers would be larger than the known universe and dwarf popular large numbers such as googol and googolplex (10100 and 10(10100)), respectively). These large numbers, although nearly impossible to comprehend, are still not at the “end” of the real numbers, which have no end. Consider the function f(x) = x2 – 10100.
a. Consider only positive values of x; how long until f(x) > 0?
Answer:
x2 > 10100
x > (10100 )(\(\frac{1}{2}\))
x > 1050
b. If your answer to part (a) represented seconds, how many billions of years would it take for f(x) > 0? (Note: One billion years is approximately 3.15×1016seconds.) How close is this to the estimated geological age of the earth (4.54 billion years)?
Answer:
1050 ÷ (3.15×1016)≈3.17×1030
It would take 3.17 thousand billion billion billion years. This is about 3.17 thousand billion billion billion years older than the earth.
c. Number theorists frequently only concern themselves with the term of a function that has the most influence as x → ∞. Let f(x) = x3 + 10x2 + 100x + 1000, and answer the following questions.
i. Fill out the following table:
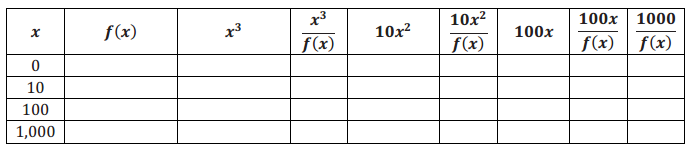
Answer:

ii. As x → ∞, which term of f dominates the value of the function?
Answer:
The term x3 grows to dominate the function. By x = 1000, x3 comprises 99% of the function’s value.
iii. Find g(x) = \(\frac{f(x)}{x}\). Which term dominates g as x → ∞?
Answer:
g(x) = x2 + 10x + 100 + \(\frac{1000}{x}\)
Again, the leading term dominates the function as x → ∞.
d. Consider the formula for a general polynomial, f(x) = anxn + an – 1x(n – 1) + ⋯ + a1x + a0 for real numbers a_i, 0≤i≤n. Which single term dominates the value of f as x → ∞?
Answer:
The leading term dominates the function as x → ∞.
Eureka Math Precalculus Module 3 Lesson 14 Exit Ticket Answer Key
Question 1.
Sketch the graph of y = \(\frac{x – 3}{x^{2} + x – 12}\). Label horizontal and vertical asymptotes, and identify any discontinuities, x – intercepts, and the y – intercept if they exist. Describe the end behavior of the function.
Answer:
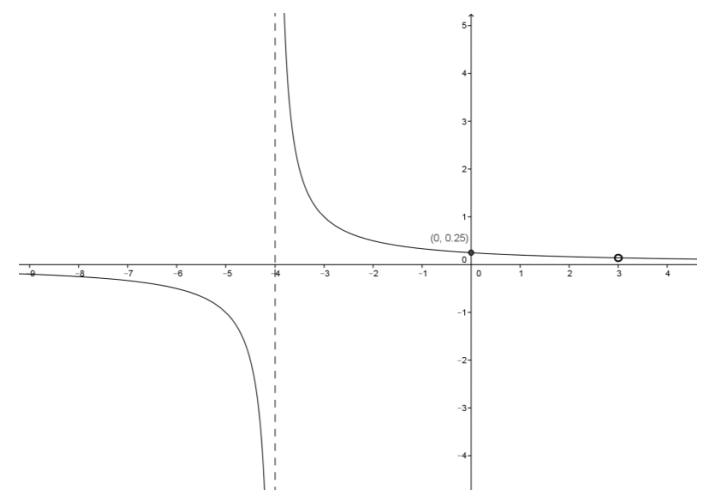
Horizontal asymptote at y = 0; vertical asymptote at x = – 4; y – intercept at (0,1/4); no x – intercepts; discontinuity at x = 3; as x → ±∞, y → 0.
Question 2.
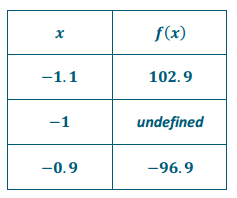
Does the graph of the function f(x) = \(\frac{x^{2} – 8 x – 9}{x + 1}\) have a vertical asymptote or a point missing at x = – 1? Explain your reasoning, and support your answer numerically.
Answer:
The graph of f has a point missing at x = – 1. I knew this because the function can simplify to f(x) = x – 9, x ≠ – 1, which means the graph looks like the line y = x – 9 at every x – value except x = – 1. This can also be seen by analyzing a table of values.

As x → – 1, f(x) → – 10, which means the graph does not have a vertical asymptote at x = – 1.