Engage NY Eureka Math Precalculus Module 3 Lesson 13 Answer Key
Eureka Math Precalculus Module 3 Lesson 13 Example Answer Key
Example
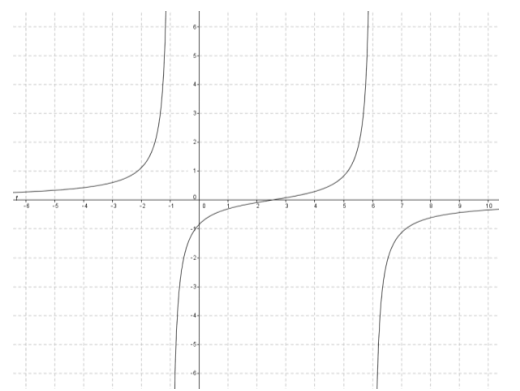
Consider the rational function f(x) = \( = \frac{2 x – 1}{x – 4}\).
a. State the domain of f.
Answer:
D: set of all real numbers except x = 4
b. Determine the end behavior of f.
Answer:
End behavior: As x → ∞,y → 2. As x → – ∞,y → 2.
c. State the horizontal asymptote of the graph of y = f(x).
Answer:
Horizontal asymptote: y = 2
d. Graph the function on the graphing calculator, and make a sketch on your paper.
Answer:
Eureka Math Precalculus Module 3 Lesson 13 Exercise Answer Key
Opening Exercise
Determine the end behavior of each rational function below. Graph each function on the graphing calculator, and explain how the graph supports your analysis of the end behavior.
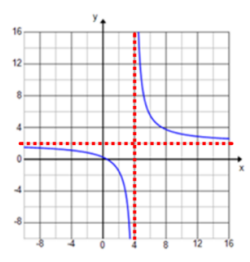
a. f(x) = \(\frac{x^{2} – 3}{x^{3}}\)
Answer:
End behavior: As x → ∞, f(x) → 0. As x → – ∞, f(x) → 0.
Looking at the ends of the graph, as x goes to ∞ or – ∞, y gets closer to 0.
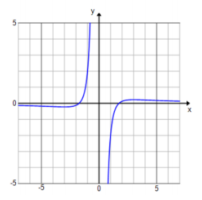
b. f(x) = \(\frac{x^{2} – 3}{x^{2} + 1}\)
Answer:
End behavior: As x → ∞, f(x) → 1. As x → – ∞, f(x) → 1.
Looking at the ends of the graph, as x goes to ∞ or – ∞, y gets closer to 1.
c. f(x) = \(\frac{x^{3}}{x^{2} – 3}\)
Answer:
End behavior: As x → ∞, f(x) → ∞, and as x → – ∞, f(x) → – ∞.
Looking at the ends of the graph, as x goes to ∞, y continues to increase toward ∞, and as x goes to – ∞, y continues to decrease toward – ∞.
Exercises
State the domain and end behavior of each rational function. Identify all horizontal and vertical asymptotes on the graph of each rational function. Then, verify your answer by graphing the function on the graphing calculator.
Exercise 1.
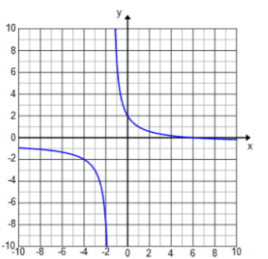
f(x) = \(\frac{ – x + 6}{2 x + 3}\)
D: set of all real numbers except x = – \(\frac{3}{2}\)
Vertical asymptotes: x = – \(\frac{3}{2}\)
End behavior: As → ∞, y → – \(\frac{1}{2}\). As → – ∞, y → – \(\frac{1}{2}\).
Horizontal asymptote: y = – \(\frac{1}{2}\)
Exercise 2.
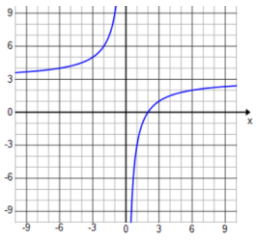
f(x) = \(\frac{3 x – 6}{x}\)
Answer:
D: set of all real numbers except x = 0
Vertical asymptotes: x = 0
End behavior: As x → ∞, y → 3. As x → – ∞, y → 3.
Horizontal asymptote: y = 3
Exercise 3.
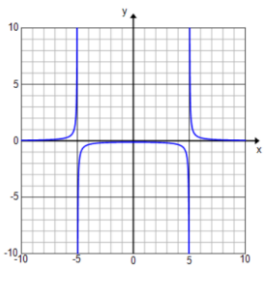
f(x) = \(\frac{3}{x^{2} – 25}\)
Answer:
D: set of all real numbers except x = – 5, 5
Vertical asymptotes: x = – 5 and x = 5
End behavior: As x → ∞, y → 0. As x → – ∞, y → 0.
Horizontal asymptote: y = 0
Exercise 4.
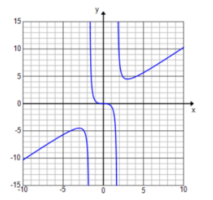
f(x) = \(\frac{x^{2} – 2}{x^{2} + 2 x – 3}\)
Answer:
D: set of all real numbers except x = – 3, 1
Vertical asymptotes: x = – 3 and x = 1
End behavior: As x → ∞, y → 1. As x → – ∞, y → 1.
Horizontal asymptote: y = 1
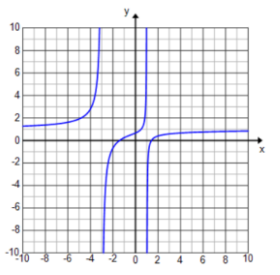
Exercise 5.
f(x) = \(\frac{x^{2} – 5 x – 4}{x + 1}\)
Answer:
D: set of all real numbers except x = – 1
Vertical asymptote: x = – 1
End behavior: As x → ∞, y → ∞. As x → – ∞, y → – ∞.
Horizontal asymptote: none
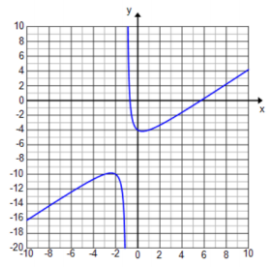
Exercise 6.
f(x) = \(\frac{5 x}{x^{2} + 9}\)
Answer:
D: set of all real numbers
Vertical asymptote: none
End behavior: As x → ∞, y → 0. As x → – ∞, y → 0.
Horizontal asymptote: y = 0
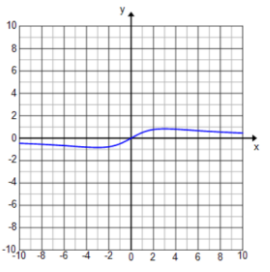
Write an equation for a rational function whose graph has the given characteristic. Graph your function on the graphing calculator to verify.
Exercise 7.
A horizontal asymptote of y = 2 and a vertical asymptote of x = – 2
Answer:
f(x) = \(\frac{2 x + 5}{x + 2}\)
Exercise 8.
A vertical asymptote of x = 6 and no horizontal asymptote
Answer:
f(x) = \(\frac{x^{2}}{x – 6}\)
Exercise 9.
A horizontal asymptote of y = 6 and no vertical asymptote
Answer:
f(x) = \(\frac{6 x^{2}}{x^{2} + 1}\)
Eureka Math Precalculus Module 3 Lesson 13 Problem Set Answer Key
Question 1.
State the domain of each rational function. Identify all horizontal and vertical asymptotes on the graph of each rational function.
a. y = \(\frac{3}{x^{3} – 1}\)
Answer:
The domain is all real numbers except x = 1, which is a vertical asymptote. The horizontal asymptote is y = 0.
b. y = \(\frac{2 x + 2}{x – 1}\)
Answer:
The domain is all real numbers except x = 1, which is a vertical asymptote. The graph of the function has a horizontal asymptote at y = 2.
c. y = \(\frac{5 x^{2} – 7 x + 12}{x^{3}}\)
Answer:
The domain is all real numbers except x = 0, which is a vertical asymptote. The horizontal asymptote occurs at y = 0.
d. y = \(\frac{3 x^{6} – 2 x^{3} + 1}{16 – 9 x^{6}}\)
Answer:
The domain is all real numbers except x = ±\(\sqrt[3]{\frac{4}{3}}\), which are both vertical asymptotes. The horizontal asymptote is y = – \(\frac{1}{3} .\).
e. f(x) = \(\frac{6 – 4 x}{x + 5}\)
Answer:
The domain is all real numbers except x = – 5, which is a vertical asymptote. The horizontal asymptote is the line y = – 4.
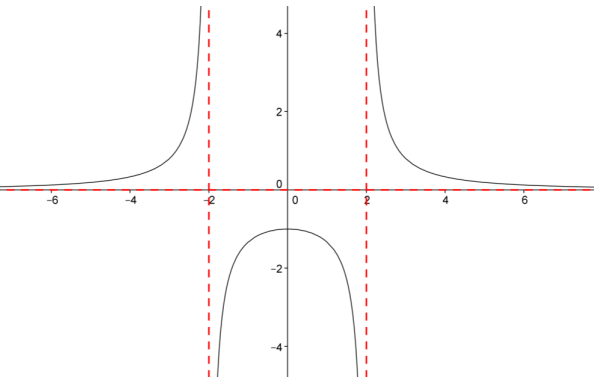
f. f(x) = \(\frac{4}{x^{2} – 4}\)
Answer:
The domain is all real numbers except x = – 2 and x = 2, which are both vertical asymptotes. The horizontal asymptote is the line y = 0.
Question 2.
Sketch the graph of each function in Exercise 1 with asymptotes and excluded values from the domain drawn on the graph.
Answer:
a.
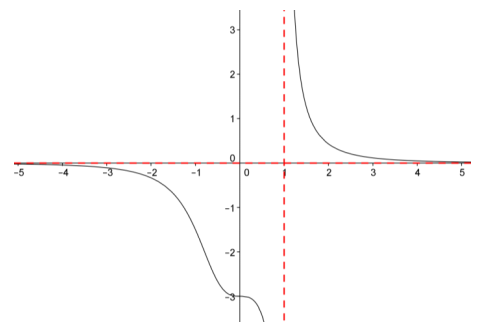
b.
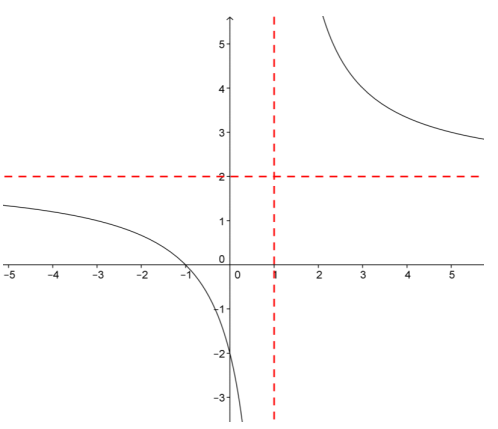
c.
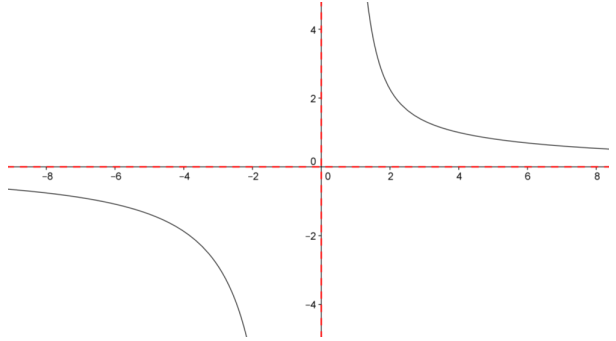
d.
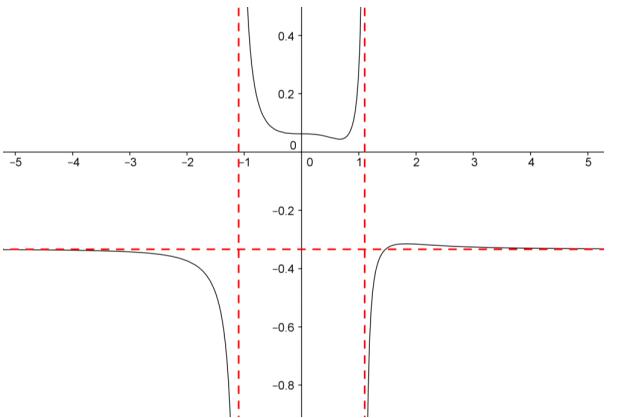
e.
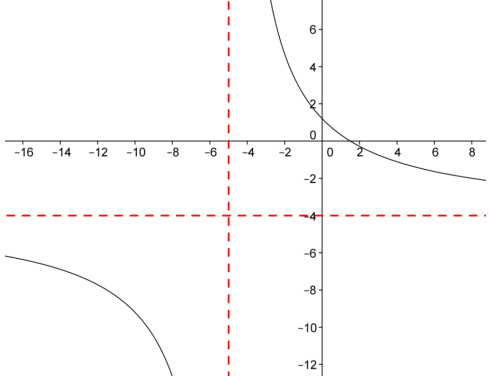
f.
Question 3.
Factor out the highest power of x in each of the following, and cancel common factors if you can. Assume x is nonzero.
a. y = \(\frac{x^{3} + 3 x – 4}{3 x^{3} – 4 x^{2} + 2 x – 5}\)
Answer:
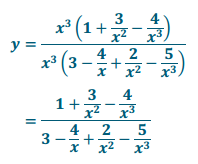
b. y = \(\frac{x^{3} – x^{2} – 6 x}{x^{3} + 5 x^{2} + 6 x}\)
Answer:
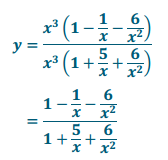
c. y = \(\frac{2 x^{4} – 3 x + 1}{5 x^{3} – 8 x – 1}\)
Answer:
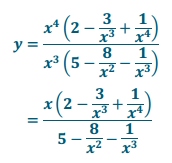
d. y = – \(\frac{9 x^{5} – 8 x^{4} + 3 x + 72}{7 x^{5} + 8 x^{4} + 8 x^{3} + 9 x^{2} + 10 x}\)
Answer:

e. y = \(\frac{3 x}{4 x^{2} + 1}\)
Answer:
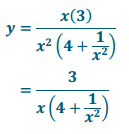
Question 4.
Describe the end behavior of each function in Exercise 3.
Answer:
a. As x → ±∞, y → \(\frac{1}{3}\).
b. As x → ±∞, y → 1.
c. As x → ±∞, y → ±∞.
d. As x → ±∞, y → – \(\frac{9}{7}\).
e. As x → ±∞, y → 0.
Question 5.
Using the equations that you wrote in Exercise 3, make some generalizations about how to quickly determine the end behavior of a rational function.
Answer:
The coefficients on the leading terms always end up being the horizontal asymptotes when the functions have the same power. When the power in the numerator is larger, then the functions either increase or decrease without bound as x increases or decreases without bound. When the power in the denominator is larger, then the functions go to zero.
Question 6.
Describe how you may be able to use the end behavior of the graphs of rational functions, along with the excluded values from the domain and the equations of any asymptotes, to graph a rational function without technology.
Answer:
Let f be a rational function. The end behavior of the graph of y = f(x) tells you in what direction the graph of f is heading, and the process of finding the end behavior yields a simpler function that f gets close to as x increases in magnitude. The vertical asymptotes and excluded values from the domain tell you where the graph varies close to the origin. All of this information combined gives you a very good idea of what the graph of f looked like without technology.
Eureka Math Precalculus Module 3 Lesson 13 Exit Ticket Answer Key
Consider the function f(x) = \(\frac{ – 2 x + 5}{x^{2} – 5 x – 6}\).
Question 1.
Looking at the structure of the function, what information can you gather about the graph of f?
Answer:
The graph has a horizontal asymptote at y = 0 because the denominator has a higher exponent than the numerator. There are two values of x that cause the denominator to equal zero, so the graph potentially has two vertical asymptotes.
Question 2.
State the domain of f.
Answer:
D: the set of all real numbers except x = 6, – 1
Question 3.
Determine the end behavior of f.
Answer:
End behavior: As x → ∞, y → 0. As x → – ∞, y → 0.
Question 4.
State the equations of any vertical and horizontal asymptotes on the graph of y = f(x).
Answer:
Vertical asymptotes: x = 6 and x = – 1
Horizontal asymptote: y = 0