Engage NY Eureka Math Precalculus Module 2 Lesson 9 Answer Key
Eureka Math Precalculus Module 2 Lesson 9 Exercise Answer Key
Opening Exercise
Recall from Problem 1, part (d), of the Problem Set of Lesson 7 that if you know what a linear transformation does to the three points (1,0,0), (0,1,0), and (0,0,1), you can find the matrix of the transformation. How do the images of these three points lead to the matrix of the transformation?
a. Suppose that a linear transformation L1 rotates the unit cube by 90° counterclockwise about the z-axis. Find the matrix A1 of the transformation L1.
Answer:
Since this transformation rotates by 90° counterclockwise in the xy-plane, a vector along the positive x-axis will be transformed to lie along the positive y-axis, a vector along the positive y-axis will be transformed to lie along the negative x-axis, and a vector along the z-axis will be left alone. Thus,
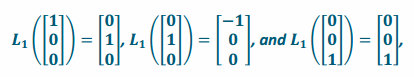
so the matrix of the transformation is A1=\(\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right] .\)
b. Suppose that a linear transformation L2 rotates the unit cube by 90° counterclockwise about the y-axis. Find the matrix A2 of the transformation L2.
Answer:
Since this transformation rotates by 90° counterclockwise in the xz-plane, a vector along the positive x-axis will be transformed to lie along the positive z-axis, a vector along the y-axis will be left alone, and a vector along the positive z-axis will be transformed to lie along the negative x-axis. Thus,
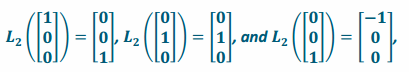
so the matrix of the transformation is A2=\(\left[\begin{array}{ccc}
0 & 0 & -1 \\
0 & 1 & 0 \\
1 & 0 & 0
\end{array}\right]\).
c. Suppose that a linear transformation L3 scales by 2 in the x-direction, scales by 3 in the y-direction, and scales by 4 in the z-direction. Find the matrix A3 of the transformation L3.
Answer:
Since this transformation scales by 2 in the x-direction, by 3 in the y-direction, and by 4 in the z-direction, a vector along the x-axis will be multiplied by 2, a vector along the y-axis will be multiplied by 3, and a vector along the z-axis will be multiplied by 4. Thus,
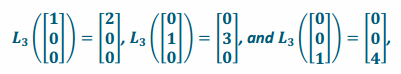
so the matrix of the transformation is A3=\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 4
\end{array}\right]\).
d. Suppose that a linear transformation L4 projects onto the xy-plane. Find the matrix A4 of the transformation L4.
Answer:
Since this transformation projects onto the xy-plane, a vector along the x-axis will be left alone, a vector along the y-axis will be left alone, and a vector along the z-axis will be transformed into the zero vector. Thus,
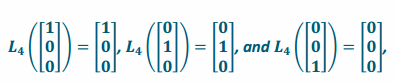
so the matrix of the transformation is A4=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]\).
e. Suppose that a linear transformation L5 projects onto the xz-plane. Find the matrix A5 of the transformation L5.
Answer:
Since this transformation projects onto the xz-plane, a vector along the x-axis will be left alone, a vector along the y-axis will be transformed into the zero vector, and a vector along the z-axis will be left alone. Thus,
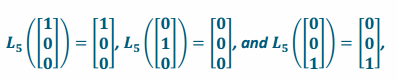
so the matrix of the transformation is A5=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\).
f. Suppose that a linear transformation L6 reflects across the plane with equation y=x. Find the matrix A6 of the transformation L6.
Answer:
Since this transformation reflects across the plane y=x, a vector along the positive x-axis will be transformed into a vector along the positive y-axis with the same length, a vector along the positive y-axis will be transformed into a vector along the positive x-axis, and a vector along the z-axis will be left alone. Thus,
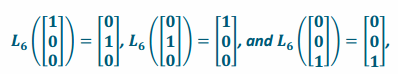
so the matrix of the transformation is A6=\(\left[\begin{array}{lll}
0 & 1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\).
g. Suppose that a linear transformation L7 satisfies 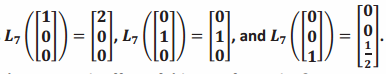 Find the matrix A7 of the transformation L7. What is the geometric effect of this transformation?
Find the matrix A7 of the transformation L7. What is the geometric effect of this transformation?
Answer:
The matrix of this transformation is 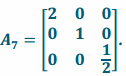 . The geometric effect of L7 is to stretch by a factor of 2 in the x-direction and scale by a factor of \(\frac{1}{2}\) in the z-direction.
. The geometric effect of L7 is to stretch by a factor of 2 in the x-direction and scale by a factor of \(\frac{1}{2}\) in the z-direction.
h. Suppose that a linear transformation L8 satisfies 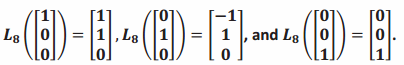 . Find the matrix of the transformation L8. What is the geometric effect of this transformation?
. Find the matrix of the transformation L8. What is the geometric effect of this transformation?
Answer:
The matrix of this transformation is 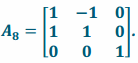 . The geometric effect of L8 is to rotate by 45° in the xy-plane, to scale by \(\sqrt{2}\) in both the x and y directions, and to not change in the z-direction.
. The geometric effect of L8 is to rotate by 45° in the xy-plane, to scale by \(\sqrt{2}\) in both the x and y directions, and to not change in the z-direction.
Eureka Math Precalculus Module 2 Lesson 9 Exploratory Challenge Answer Key
Exploratory Challenge 1
Transformations L1–L8 refer to the linear transformations from the Opening Exercise. For each pair:
i. Make a conjecture to predict the geometric effect of performing the two transformations in the order specified.
ii. Find the product of the corresponding matrices in the order that corresponds to the indicated order of composition. Remember that if we perform a transformation LB with matrix B and then LA with matrix A, the matrix that corresponds to the composition LA∘LB is AB. That is, LB is applied first, but matrix B is written second.
iii. Use the GeoGebra applet TransformCubes.ggb to draw the image of the unit cube under the transformation induced by the matrix product in part (ii). Was your conjecture in part (i) correct?
a. Perform L6 and then L6.
Answer:
i. Since L6 reflects across the plane through y=x that is perpendicular to the xy-plane, performing L6 twice in succession will result in the identity transformation.
ii. A6⋅A6=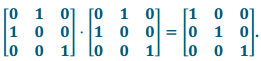 . Since A6⋅A6 is the identity matrix, we know that
. Since A6⋅A6 is the identity matrix, we know that
L6∘L6 is the identity transformation.
iii. The conjecture was correct.
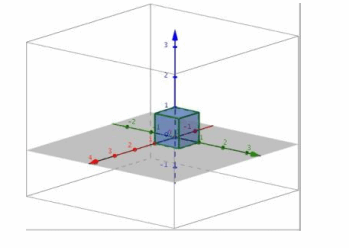
b. Perform L1 and then L2.
Answer:
i. Sample student response: Since L1 rotates 90° about the z-axis and L2 rotates 90° about the y-axis, the composition L2∘L1 should rotate 180° about the line y=-x in the xy-plane.
ii. 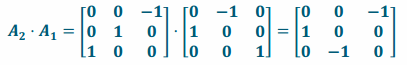
iii. The conjecture in part (i) is not correct. While it appears that the composition L2∘L1 is a rotation by 180° about the line y=-x, it is not because, for example, point (0,1,0) is transformed to point (0,0,-1) and does not remain on the y-axis after the transformation. Thus, this cannot be a rotation around the y-axis.
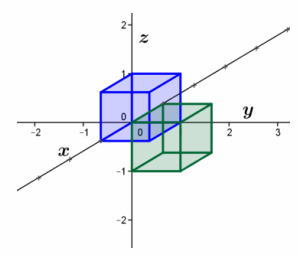
c. Perform L4 and then L5.
Answer:
i. Since L4 projects onto the xy-plane and L5 projects onto the xz-plane, the composition L5∘L4 will project onto the x-axis.
ii. 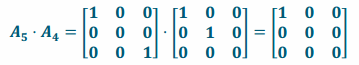
iii. The conjecture in part (i) is correct. The cube is first transformed to a square in the xy-plane and then transformed onto a segment on the x-axis.
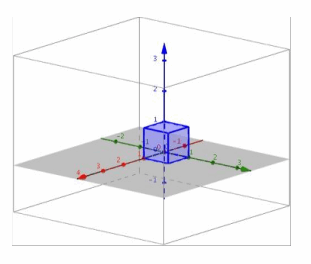
d. Perform L4 and then L3.
Answer:
i. Since L4 projects onto the xy-plane and L3 scales in the x, y, and z directions, the composition L3∘L4 will project onto the xy-plane and scale in the x and y directions.
ii. 
iii. The conjecture in part (i) is correct.
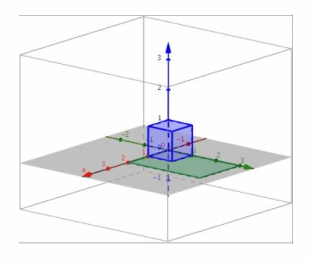
e. Perform L3 and then L7.
Answer:
i. Since L3 scales in the x, y, and z directions and so does L7, the composition will be a transformation that also scales in all three directions but with different scale factors.
ii. 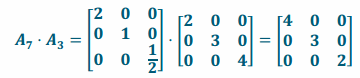
iii. The conjecture from (i) is correct.
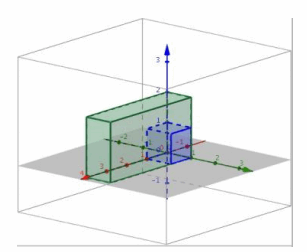
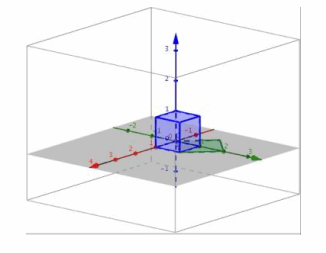
f. Perform L8 and then L4.
Answer:
i. Transformation L8 rotates the unit cube by 45° about the z-axis and stretches by a factor of \(\sqrt{2}\) in both the x and y directions, while L4 projects the image onto the xy-plane. The composition will transform the unit cube into a larger square that has been rotated 45° in the xy-plane.
ii. 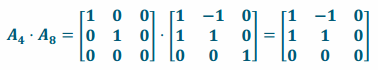
iii. The conjecture from part (i) is correct.
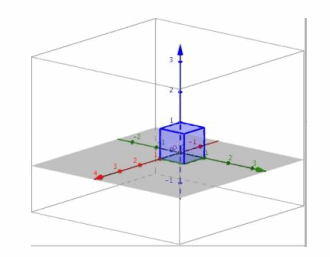
g. Perform L4 and then L6.
Answer:
i. Transformation L4 projects onto the xy-plane, and transformation L6 reflects across the plane through the line y=x in the xy-plane and is perpendicular to the xy-plane, so the composition L6∘L4 will appear to be the reflection in the xy-plane across the line y=x.
ii. 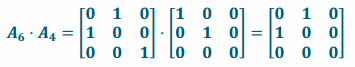
iii. The conjecture in part (i) is correct.
h. Perform L2 and then L7.
Answer:
i. Since L2 rotates 90° around the y-axis and L7 scales in the x and z directions, the composition L7∘L2 will rotate and scale simultaneously.
ii. 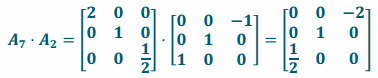
iii. The conjecture in part (i) is correct.
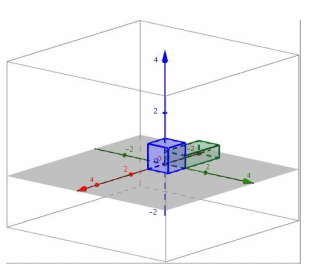
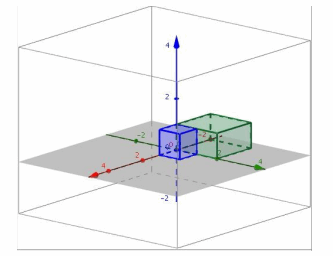
i. Perform L8 and then L8.
Answer:
i. Since L8 rotates by 45° about the z-axis and scales by \(\sqrt{2}\) in the x and y directions, performing this transformation twice will rotate by 90° about the z-axis and scale by 2 in the x and y directions.
ii. 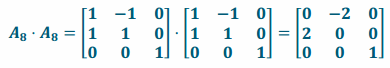
iii. The conjecture in part (i) is correct.
Exploratory Challenge 2
Transformations L1–L8 refer to the transformations from the Opening Exercise. For each of the following pairs of matrices A and B below, compare the transformations LA∘LB and LB∘LA.
a. L4 and L5
Answer:
Transformation L4∘L5 has matrix representation A4⋅A5= 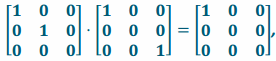 and transformation L5∘L4 has matrix representation
and transformation L5∘L4 has matrix representation 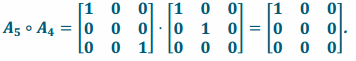
Since the two transformations have the same matrix representation, they are the same transformation:
L5∘L4=L4∘L5
b. L2 and L5
Answer:
Transformation L2 \(\text { o }\) L5 has matrix representation 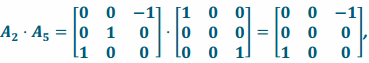 and
and
transformation L5 \(\text { o }\) L2 has matrix representation A5∙A2 =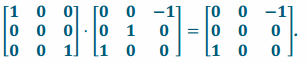
Since the two transformations have the same matrix representation, they are the same transformation:
L2 \(\text { o }\)L5 = L5 \(\text { o }\) L2
c. L3 and L7
Answer:
Transformation L3∘L7 has matrix representation 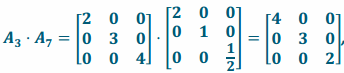 and transformation as matrix representation
and transformation as matrix representation 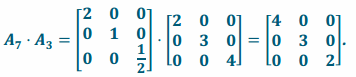
Since the two transformations have the same matrix representation, they are the same transformation:
L3\(\text { o }\)L7=L7\(\text { o }\)L3
d. L3 and L6
Answer:
Transformation L3\(\text { o }\)L6 has matrix representation 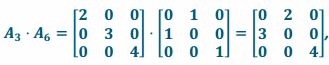 and transformation L6\(\text { o }\)L3 has matrix representation
and transformation L6\(\text { o }\)L3 has matrix representation 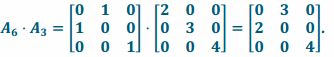
Since the two transformations have different matrix representations, they are not the same transformation: L3∘L6≠L6∘L3
e. L7 and L1
Answer:
Transformation L7\(\text { o }\)L1 has matrix representation 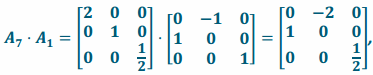 and transformation L1∘L7 has matrix representation
and transformation L1∘L7 has matrix representation 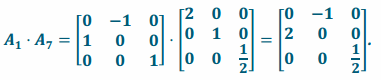
Since the two transformations have different matrix representations, they are not the same transformation: L1∘L7≠L7∘L1
f. What can you conclude about the order in which you compose two linear transformations?
Answer:
In some cases, the order of composition of two linear transformations matters. For two matrices A and B, the transformation LA∘LB is not always the same transformation as LB∘LA.
Eureka Math Precalculus Module 2 Lesson 9 Problem Set Answer Key
Question 1.
Let A be the matrix representing a dilation of \(\frac{1}{2}\), and let B be the matrix representing a reflection across the
yz-plane.
a. Write A and B.
Answer:
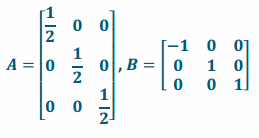
b. Evaluate AB. What does this matrix represent?
Answer:
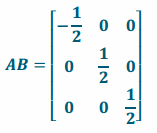
AB is a reflection across the yz-plane followed by a dilation of \(\frac{1}{2}\).
c. Let x=\(\left[\begin{array}{l}
5 \\
6 \\
4
\end{array}\right]\), y=\(\left[\begin{array}{l}
-1 \\
3 \\
2
\end{array}\right]\), and z=\(\left[\begin{array}{l}
8 \\
-2 \\
-4
\end{array}\right]\). Find (AB)x, (AB)y, and (AB)z.
Answer:
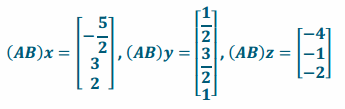
Question 2.
Let A be the matrix representing a rotation of 30° about the x-axis, and let B be the matrix representing a dilation of 5.
a. Write A and B.
Answer:
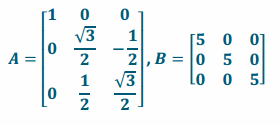
b. Evaluate AB. What does this matrix represent?
Answer:
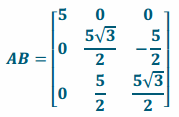
AB is a dilation of 5 followed by a rotation of 30° about the x-axis.
c. Let x=\(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\), y=\(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\), z=\(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\). Find (AB)x, (AB)y, and (AB)z.
Answer:
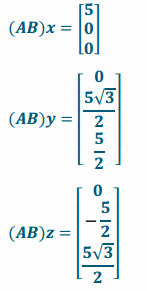
Question 3.
Let A be the matrix representing a dilation of 3, and let B be the matrix representing a reflection across the plane y=x.
a. Write A and B.
Answer:
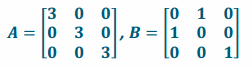
b. Evaluate AB. What does this matrix represent?
Answer:
AB=\(\left[\begin{array}{lll}
0 & 3 & 0 \\
3 & 0 & 0 \\
0 & 0 & 3
\end{array}\right]\)
AB is a reflection across the y=x plane followed by a dilation of 3.
c. Let x=\(\left[\begin{array}{c}
-2 \\
7 \\
3
\end{array}\right]\). Find (AB)x.
Answer:
(AB)x=\(\left[\begin{array}{c}
21 \\
-6 \\
9
\end{array}\right]\)
Question 4.
Let A=\(\left[\begin{array}{lll}
3 & 0 & 0 \\
3 & 3 & 0 \\
0 & 0 & 1
\end{array}\right]\), B=\(\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{ccc}
0 & -3 & 0 \\
3 & -3 & 0 \\
0 & 0 & 1
\end{array}\right]\)
b. Let x=\(\left[\begin{array}{c}
-2 \\
2 \\
5
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
-6 \\
-12 \\
5
\end{array}\right]\)
c. Graph x and (AB)x.
Answer:
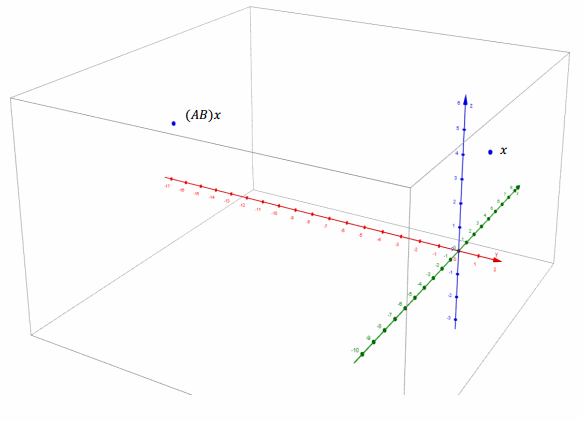
Question 5.
Let A=\(\left[\begin{array}{lll}
\frac{1}{3} & 0 & 0 \\
0 & 1 & 0 \\
2 & 0 & \frac{1}{3}
\end{array}\right]\), B=\(\left[\begin{array}{ccc}
3 & 1 & 0 \\
1 & -3 & 0 \\
0 & 0 & 1
\end{array}\right]\)
a. Evaluate AB.
Answer:
\(\left[\begin{array}{ccc}
1 & \frac{1}{3} & 0 \\
1 & -3 & 0 \\
6 & 2 & \frac{1}{3}
\end{array}\right]\)
b. Let x=\(\left[\begin{array}{l}
\mathbf{0} \\
3 \\
2
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
1 \\
-9 \\
\frac{20}{3}
\end{array}\right]\)
c. Graph x and (AB)x.
Answer:
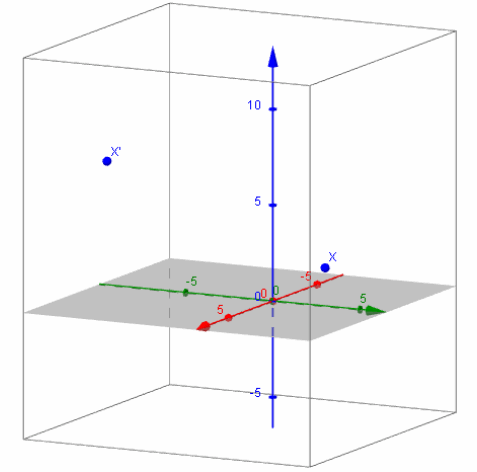
Question 6.
Let A=\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 8
\end{array}\right]\), B=\(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0
\end{array}\right]\).
a. Evaluate AB.
Answer:
\(\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 3 & 0 \\
0 & 0 & 0
\end{array}\right]\)
b. Let x=\(\left[\begin{array}{c}
1 \\
-2 \\
4
\end{array}\right]\). Find (AB)x.
Answer:
\(\left[\begin{array}{c}
2 \\
-6 \\
0
\end{array}\right]\)
c. Graph x and (AB)x.
Answer:
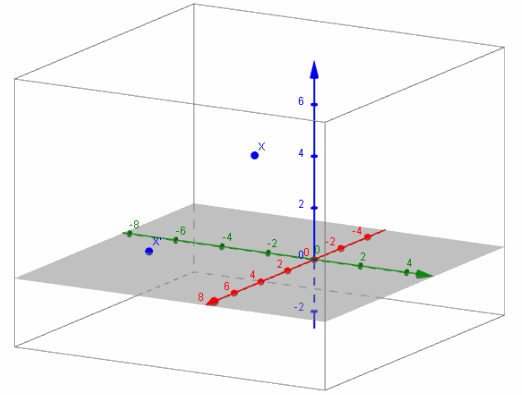
d. What does AB represent geometrically?
Answer:
AB represents a projection onto the xy-plane, and a dilation of 2 in the x-direction and 3 in the y-direction.
Question 7.
Let A, B, C be 3×3 matrices representing linear transformations.
a. What does A(BC) represent?
Answer:
The linear transformation of applying the linear transformation that C represents followed by the transformation that B represents followed by the transformation that A represents
b. Will the pattern established in part (a) be true no matter how many matrices are multiplied on the left?
Answer:
Yes, in general. When you multiply by a matrix on the left, you are applying a linear transformation after all linear transformations to the right have been applied.
c. Does (AB)C represent something different from A(BC)? Explain.
Answer:
No, it does not. This is the linear transformation obtained by applying C and then AB, which is B followed by A.
Question 8.
Let AB represent any composition of linear transformations in R3. What is the value of (AB)x where x=\(\left[\begin{array}{l}
\mathbf{0} \\
\mathbf{0} \\
\mathbf{0}
\end{array}\right]\)?
Answer:
Since a composition of linear transformations in R3 is also a linear transformation, we know that applying it to the origin will result in no change.
Eureka Math Precalculus Module 2 Lesson 9 Exit Ticket Answer Key
Let A be the matrix representing a rotation about the z-axis of 45° and B be the matrix representing a dilation of 2.
a. Write down A and B.
Answer:
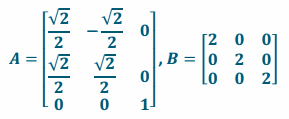
b. Let x=\(\left[\begin{array}{c}
3 \\
-1 \\
2
\end{array}\right]\). Find the matrix representing a dilation of x by 2 followed by a rotation about the z-axis of 45°.
Answer:
AB=\(\left[\begin{array}{ccc}
\sqrt{2} & -\sqrt{2} & 0 \\
\sqrt{2} & \sqrt{2} & 0 \\
0 & 0 & 2
\end{array}\right]\)
c. Do your best to sketch a picture of x, x after the first transformation, and x after both transformations. You may use technology to help you.
Answer: