Engage NY Eureka Math Precalculus Module 2 Lesson 21 Answer Key
Eureka Math Precalculus Module 2 Lesson 21 Exercise Answer Key
Opening Exercise
a. Find three different ways to write the equation that represents the line in the plane that passes through points (1, 2) and (2, – 1).
Answer:
The following four equations show different forms of the equation that represents the line through
(1, 2) and (2, – 1).
(y – 2) = – 3(x – 1)
y + 1 = – 3(x – 2)
y = – 3x + 5
3x + y = 5
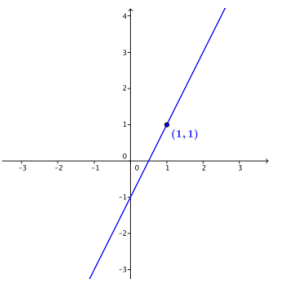
b. Graph the line through point (1, 1) with slope 2.
Answer:
Exercises
Exercise 1.
Consider the line l in the plane given by the equation 3x – 2y = 6.
a. Sketch a graph of line l on the axes provided.
Answer:
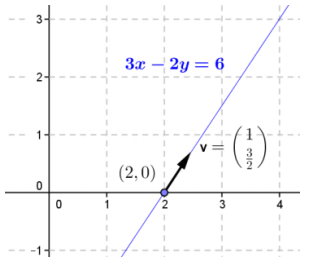
b. Find a point on line l and the slope of line l.
Answer:
Student responses for the point will vary; common choices include (0, – 3) or (2, 0). The slope of the line is \(\frac{3}{2}\).
c. Write a vector equation for line l using the information you found in part (b).
Answer:
Student responses will vary. Sample responses are
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
0 \\
– 3
\end{array}\right] + \left[\begin{array}{c}
1 \\
1.5
\end{array}\right] t\)
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
0
\end{array}\right] + \left[\begin{array}{c}
1 \\
1.5
\end{array}\right] t\)
d. Write parametric equations for line l.
Answer:
Student responses will vary. Sample responses are
x(t) = t
y(t) = – 3 + 1.5t
or
x(t) = 2 + t
y(t) = 1.5t.
e. Verify algebraically that your parametric equations produce points on line l.
Answer:
3x – 2y = 3(t) – 2( – 3 + 1.5t)
= 3t + 6 – 3t
= 6
Thus, the parametric equations x(t) = t and y(t) = – 3 + 1.5t produce points on line l.
Exercise 2.
Olivia wrote parametric equations x(t) = 4 + 2t and y(t) = 3 + 3t. Are her equations correct? What did she do differently from you?
Answer:
Her equations are also correct:
3x – 2y = 3(4 + 2t) – 2(3 + 3t)
= 12 + 6t – 6 – 6t
= 6.
She chose the point (4, 3) on the line and used the vector \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\).
Exercise 3.
Convert the parametric equations x(t) = 2 – 3t and y(t) = 4 + t into slope – intercept form.
Answer:
One vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
4
\end{array}\right] + \left[\begin{array}{c}
– 3 \\
1
\end{array}\right] t\), so the line passes through (2, 4) with slope m = – \(\frac{1}{3}\). Then the line has equation
y – 4 = – \(\frac{1}{3}\) (x – 2)
y = – \(\frac{1}{3}\) x + \(\frac{2}{3}\) + 4
y = – \(\frac{1}{3}\) x + \(\frac{14}{3}\).
Exercise 4.
Find parametric equations to represent the line that passes through point (4, 2, 9) and has direction vector
v = \(\left[\begin{array}{c}
2 \\
– 1 \\
– 3
\end{array}\right]\)
Answer:
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
4 \\
2 \\
9
\end{array}\right] + \left[\begin{array}{c}
2 \\
– 1 \\
– 3
\end{array}\right] t\)
x(t) = 4 + 2t
y(t) = 2 – t
z(t) = 9 – 3t
Exercise 5.
Find a vector form of the equation of the line given by the parametric equations
x(t) = 3t
y(t) = – 4 – 2t
z(t) = 3 – t.
Answer:
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{c}
0 \\
– 4 \\
3
\end{array}\right] + \left[\begin{array}{c}
3 \\
– 2 \\
– 1
\end{array}\right] \boldsymbol{t}\)
Eureka Math Precalculus Module 2 Lesson 21 Problem Set Answer Key
Question 1.
Find three points on the line in the plane with parametric equations x(t) = 4 – 3t and y(t) = 1 + \(\frac{1}{3}\)t.
Answer:
Student responses will vary. Using t = 0, t = 3, and t = – 3 gives the three points (4, 1), ( – 5, 4) and (13, 0).
Question 2.
Find vector and parametric equations to represent the line in the plane with the given equation.
a. y = 3x – 4
Answer:
Since the slope is 3 = \(\frac{3}{1}\)and a point on the line is (0, – 4), a vector form of the equation is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
0 \\
– 4
\end{array}\right] + \left[\begin{array}{l}
1 \\
3
\end{array}\right] t\). Then the parametric equations are x(t) = t and y = – 4 + 3t.
b. 2x – 5y = 10
Answer:
First, we rewrite the equation of the line in slope – intercept form: y = \(\frac{2}{5}\) x – 2. Since the slope is \(\frac{2}{5}\) and a point on the line is (0, – 2), a vector form of the equation is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
0 \\
– 2
\end{array}\right] + \left[\begin{array}{l}
5 \\
2
\end{array}\right] t\). Then the parametric equations are x(t) = 5t and y = – 2 + 2t.
c. y = – x
Answer:
Since the slope is – 1 and a point on the line is (0, 0), a vector form of the equation is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
0
\end{array}\right] + \left[\begin{array}{c}
1 \\
– 1
\end{array}\right] t\). Then the parametric equations are x(t) = t and y = – t.
d. y – 2 = 3(x + 1)
Answer:
First, we rewrite the equation of the line in slope – intercept form: y = 3x + 5. Since the slope is 3 and a point on the line is (0, 5), a vector form of the equation is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
5
\end{array}\right] + \left[\begin{array}{l}
1 \\
3
\end{array}\right] t\). Then the parametric equations are x(t) = t and y = 5 + 3t.
Question 3.
Find vector and parametric equations to represent the following lines in the plane.
a. the x – axis
Answer:
A vector in the direction of the x – axis is \(\left[\begin{array}{l}
1 \\
0
\end{array}\right]\) and the line passes through the origin (0, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
1 \\
0
\end{array}\right] t\). Thus, the parametric equations are x(t) = t and y(t) = 0.
b. the y – axis
Answer:
A vector in the direction of the y – axis is \(\left[\begin{array}{l}
0 \\
1
\end{array}\right]\), and the line passes through the origin (0, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
1
\end{array}\right] t\). Thus, the parametric equations are x(t) = 0 and y(t) = t.
c. the horizontal line with equation y = 4
Answer:
A vector in the direction of the line is \(\left[\begin{array}{l}
1 \\
0
\end{array}\right]\) and the line passes through (0, 4), so a vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
4
\end{array}\right] + \left[\begin{array}{l}
1 \\
0
\end{array}\right] t\). Thus, the parametric equations are x(t) = t and y(t) = 4.
d. the vertical line with equation x = – 2
Answer:
A vector in the direction of the line is \(\left[\begin{array}{l}
0 \\
1
\end{array}\right]\) and the line passes through ( – 2, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
– 2 \\
0
\end{array}\right] + \left[\begin{array}{l}
0 \\
1
\end{array}\right] t\). Thus, the parametric equations are x(t) = – 2 and y(t) = t.
e. the horizontal line with equation y = k, for a real number k
Answer:
A vector in the direction of the line is \(\left[\begin{array}{l}
1 \\
0
\end{array}\right]\) and the line passes through (0, k), so a vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
k
\end{array}\right] + \left[\begin{array}{l}
1 \\
0
\end{array}\right] t\). Thus, the parametric equations are x(t) = t and y(t) = k.
f. the vertical line with equation x = h, for a real number h
Answer:
A vector in the direction of the line is \(\left[\begin{array}{l}
0 \\
1
\end{array}\right]\) and the line passes through (h, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
h \\
0
\end{array}\right] + \left[\begin{array}{l}
0 \\
1
\end{array}\right] t\). Thus, the parametric equations are x(t) = h and y(t) = t.
Question 4.
Find the point – slope form of the line in the plane with the given parametric equations.
a. x(t) = 2 – 4t, y(t) = 3 – 7t
Answer:
The vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right] + \left[\begin{array}{l}
– 4 \\
– 7
\end{array}\right] t\), so the line passes through the point (2, 3) with slope m = \(\frac{ – 7}{ – 4} = \frac{7}{4}\). Thus, the point – slope form of the line is y – 3 = \(\frac{7}{4}\) (x – 2).
b. x(t) = 2 – \(\) t, y(t) = 6 + 6t
Answer:
The vector form is
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
6
\end{array}\right] + \left[\begin{array}{c}
– \frac{2}{3} \\
6
\end{array}\right] t\)
so the line passes through the point (2, 6) with slope
m = \(\frac{6}{ – \frac{2}{3}}\) = – 9.
Thus, the point – slope form of the line is y – 6 = – 9(x – 2).
c. x(t) = 3 – t, y(t) = 3
Answer:
The vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
3 \\
3
\end{array}\right] + \left[\begin{array}{c}
– 1 \\
0
\end{array}\right] t\), so the line passes through the point (3, 3) with slope m = 0. Thus, the point – slope form of the line is y – 3 = 0(x – 3), which is equivalent to y = 3.
d. x(t) = t, y(t) = t
Answer:
The vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
0
\end{array}\right] + \left[\begin{array}{l}
1 \\
1
\end{array}\right] t\), so the line passes through the point (0, 0)with slope m = 1. Thus, the point – slope form of the line is y = x.
Question 5.
Find vector and parametric equations for the line in the plane through point P in the direction of vector v.
a. P = (1, 5), v = \(\left[\begin{array}{c}
2 \\
– 1
\end{array}\right]\)
Answer:
The vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
1 \\
5
\end{array}\right] + \left[\begin{array}{c}
2 \\
– 1
\end{array}\right] t\), so the parametric equations are x(t) = 1 + 2t and y(t) = 5 – t.
b. P = (0, 0), v = \(\left[\begin{array}{l}
4 \\
4
\end{array}\right]\)
Answer:
The vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
0
\end{array}\right] + \left[\begin{array}{l}
4 \\
4
\end{array}\right] t\), so the parametric equations are x(t) = 4t and y(t) = 4t.
c. P = ( – 3, – 1), v = \(\left[\begin{array}{l}
1 \\
2
\end{array}\right]\)
Answer:
The vector form is \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
– 3 \\
– 1
\end{array}\right] + \left[\begin{array}{l}
1 \\
2
\end{array}\right] t\), so the parametric equations are x(t) = – 3 + t and y(t) = – 1 + 2t.
Question 6.
Determine if the point A is on the line l represented by the given parametric equations.
a. A = (3, 1), x(t) = 1 + 2t and y(t) = 3 – 2t
Answer:
Point A is on the line if there is a single value of t so that 3 = 1 + 2t and 1 = 3 – 2t. If 1 + 2t = 3, then t = 1. If 1 = 3 – 2t, then t = 1. Thus, A is on the line given by these parametric equations.
b. A = (0, 0), x(t) = 3 + 6t and y(t) = 2 + 4t
Answer:
Point A is on the line if there is a single value of t so that 0 = 3 + 6t and 0 = 2 + 4t. If 3 + 6t = 0, then t = – \(\frac{1}{2}\). If 0 = 2 + 4t, then t = – \(\frac{1}{2}\). Thus, A is on the line given by these parametric equations.
c. A = (2, 3), x(t) = 4 – 2t and y(t) = 4 + t
Answer:
Point A is on the line if there is a single value of t so that 2 = 4 – 2t and 3 = 4 + t. If 4 – 2t = 2, then t = 1. If 3 = 4 + t, then t = – 1. Since there is no value of t that gives 4 – 2t = 2 and 3 = 4 + t, point A is not on the line.
d. A = (2, 5), x(t) = 12 + 2t and y(t) = 15 + 2t
Answer:
Point A is on the line if there is a single value of t so that 12 + 2t = 2 and 15 + 2t = 5. If 12 + 2t = 2, then t = – 5. If 15 + 2t = 5, then t = – 5. Thus, A is on the line given by these parametric equations.
Question 7.
Find three points on the line in space with parametric equations x(t) = 4 + 2t, y(t) = 6 – t, and z(t) = t.
Answer:
Student responses will vary. Using t = 0, t = 1, and t = – 1 gives the three points (4, 6, 0), (6, 5, 1), and (2, 7, – 1).
Question 8.
Find vector and parametric equations to represent the following lines in space.
a. The x – axis
Answer:
A vector in the direction of the x – axis is \(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right]\) and the line passes through the origin (0, 0, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
1 \\
0 \\
0
\end{array}\right] t\). Thus, the parametric equations are x(t) = t, y(t) = 0, and z(t) = 0.
b. The y – axis
Answer:
A vector in the direction of the y – axis is \(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right]\) and the line passes through the origin (0, 0, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
1 \\
0
\end{array}\right] t\). Thus, the parametric equations are x(t) = 0, y(t) = 1, and z(t) = 0.
c. The z – axis
Answer:
A vector in the direction of the z – axis is \(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right]\) and the line passes through the origin (0, 0, 0), so a vector form is \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
0 \\
1
\end{array}\right] t\). Thus, the parametric equations are x(t) = 0, y(t) = 0, and z(t) = 1.
Question 9.
Convert the equation given in vector form to a set of parametric equations for the line l.
a. \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right] + \left[\begin{array}{l}
2 \\
3 \\
4
\end{array}\right] t\)
Answer:
x(t) = 1 + 2t, y(t) = 1 + 3t, and z(t) = 1 + 4t
b. \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
3 \\
0 \\
0
\end{array}\right] + \left[\begin{array}{c}
0 \\
1 \\
– 2
\end{array}\right] t\)
Answer:
x(t) = 3, y(t) = t, and z(t) = – 2t
c. \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
5 \\
0 \\
2
\end{array}\right] + \left[\begin{array}{c}
4 \\
– 3 \\
– 8
\end{array}\right] t\)
Answer:
x(t) = 5 + 4t, y(t) = – 3t, and z(t) = 2 – 8t
Question 10.
Find vector and parametric equations for the line in space through point P in the direction of vector v.
a. P = (1, 4, 3), v = \(\left[\begin{array}{c}
3 \\
6 \\
– 2
\end{array}\right]\)
Answer:
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
1 \\
4 \\
3
\end{array}\right] + \left[\begin{array}{c}
3 \\
6 \\
– 2
\end{array}\right] t\); x(t) = 1 + 3t, y(t) = 4 + 6t, and z(t) = 3 – 2t
b. P = (2, 2, 2), v = \(\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right]\)
Answer:
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
2 \\
2
\end{array}\right] + \left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right] t\); x(t) = 2 + t, y(t) = 2 + t, and z(t) = 2 + t
c. P = (0, 0, 0), v = \(\left[\begin{array}{c}
4 \\
4 \\
– 2
\end{array}\right]\)
Answer:
\(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
0 \\
0
\end{array}\right] + \left[\begin{array}{c}
4 \\
4 \\
– 2
\end{array}\right] t\); x(t) = 4t, y(t) = 4t, and z(t) = – 2t
Question 11.
Determine if the point A is on the line l represented by the given parametric equations.
a. A = (3, 1, 1), x(t) = 5 – t, y(t) = – 5 + 3t, and z(t) = 9 – 4t
Answer:
If A is on line l, then there is a single value of t so that 5 – t = 3, – 5 + 3t = 1, and 9 – 4t = 1. If 5 – t = 3, then t = 2. If –5 + 3t = 1, then t = 2. If 9 – 4t = 1, then t = 2. Thus, A lies on line l.
b. A = (1, 0, 2), x(t) = 7 – 2t, y(t) = 3 – t, and z(t) = 4 – t
Answer:
If A is on line l, then there is a single value of t so that 7 – 2t = 1, 3 – t = 0, and 4 – t = 2. If 7 – 2t = 1, then t = 3. If 3 – t = 0, then t = 3. If 4 – t = 2, then t = 2. Thus, there is no value of t that satisfies all three equations, so point A is not on line l.
c. A = (5, 3, 2), x(t) = 8 + t, y(t) = – t, and z(t) = – 4 – 2t
Answer:
If A is on line l, then there is a single value of t so that 8 + t = 5, – t = 3, and – 4 – 2t = 2. If 8 + t = 5, then t = – 3. If –t = 3, then t = – 3. If – 4 – 2t = 2, then t = – 3. Thus, A lies on line l.
Eureka Math Precalculus Module 2 Lesson 21 Exit Ticket Answer Key
Question 1.
Find parametric equations for the line in the plane given by y = 2x + 3.
Answer:
This line passes through point (0, 3) with slope m = 2. Then the vector form of the line is
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
0 \\
3
\end{array}\right] + \left[\begin{array}{l}
1 \\
2
\end{array}\right] t\)
so the parametric equations are
x(t) = t
y(t) = 3 + 2t.
Question 2.
Do y = 7 – x and x(t) = – 1 and y(t) = 1 + 7t represent the same line? Explain why or why not.
Answer:
We can see that if x(t) = – 1 and y(t) = 7 – t, then 7 – x = 7 – ( – 1) = 8 so y≠7 – x, and thus the equations are not the same line.
Question 3.
Find parametric equations for the line in space that passes through point (1, 0, 4) with direction vector v = \(\left[\begin{array}{l}
3 \\
2 \\
1
\end{array}\right]\).
Answer:
x(t) = 1 + 3t
y(t) = 0 + 2t
z(t) = 4 + t.