Engage NY Eureka Math Precalculus Module 2 Lesson 2 Answer Key
Eureka Math Precalculus Module 2 Lesson 2 Exercise Answer Key
Opening Exercise
Suppose a subway line also connects the four cities. Here is the subway and bus line network. The bus routes connecting the cities are represented by solid lines, and the subway routes are represented by dashed arcs.
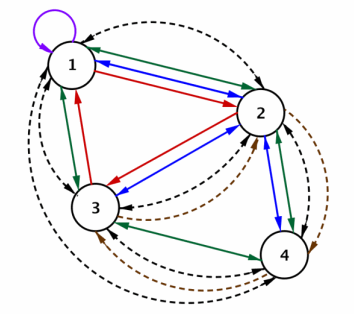
Write a matrix B to represent the bus routes and a matrix S to represent the subway lines connecting the four cities.
Answer:
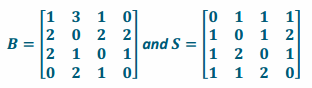
Exploratory Challenge/Exercises 1–6: Matrix Arithmetic
Use the network diagram from the Opening Exercise and your answers to help you complete this challenge with your group.
Exercise 1.
Suppose the number of bus routes between each city were doubled.
a. What would the new bus route matrix be?
Answer:
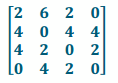
b. Mathematicians call this matrix 2B. Why do you think they call it that?
Answer:
Each entry is multiplied by 2, so the values are twice what they were before.
Exercise 2.
What would be the meaning of 10B in this situation?
Answer:
It would mean each entry in matrix B is multiplied by 10, so the city now has 10 times as many bus routes as before connecting the cities.
Exercise 3.
Write the matrix 10B.
Answer:
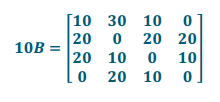
Exercise 4.
Ignore whether or not a line connecting cities represents a bus or subway route.
a. Create one matrix that represents all the routes between the cities in this transportation network.
Answer:

b. Why would it be appropriate to call this matrix B+S? Explain your reasoning.
Answer:
The total number of routes regardless of transportation mode is found by counting the total routes. We can also find that by adding the number of bus and subway lines between each pair of cities.
Exercise 5.
What would be the meaning of 4B+2S in this situation?
Answer:
It would mean the total routes connecting the cities if the number of bus lines were increased by a factor of 4 and the number of subway lines were doubled.
Exercise 6.
Write the matrix 4B+2S. Show work and explain how you found your answer.
Answer:
First multiply each entry in B by 4, and then multiply each entry in S by 2.
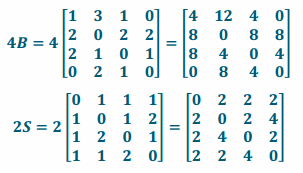
Finally, add these two new matrices together by adding corresponding entries.
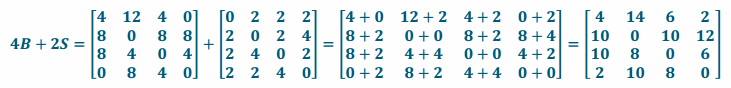
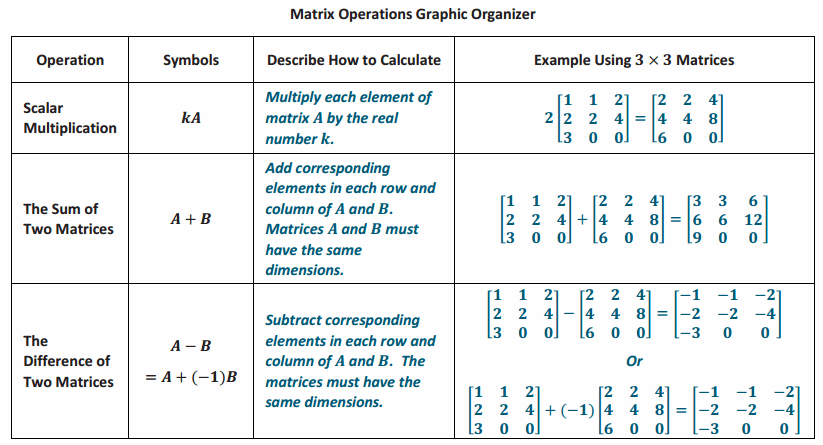
Exercise 7.
Complete this graphic organizer.
Answer:
Eureka Math Precalculus Module 2 Lesson 2 Problem Set Answer Key
Question 1.
For the matrices given below, perform each of the following calculations, or explain why the calculation is not possible.
A=\(\left[\begin{array}{ll}
1 & 2 \\
0 & 1
\end{array}\right]\)
B=\(\left[\begin{array}{cc}
2 & 1 \\
-1 & 4
\end{array}\right]\)
C=\(\left[\begin{array}{ccc}
5 & 2 & 9 \\
6 & 1 & 3 \\
-1 & 1 & 0
\end{array}\right]\)
D=\(\left[\begin{array}{ccc}
1 & 6 & 0 \\
3 & 0 & 2 \\
1 & 3 & -2
\end{array}\right]\)
a. A+B
Answer:
\(\left[\begin{array}{cc}
3 & 3 \\
-1 & 5
\end{array}\right]\)
b. 2A-B
\(\left[\begin{array}{cc}
0 & 3 \\
1 & -2
\end{array}\right]\)
c. A+C
Answer:
Matrices A and C cannot be added together because they do not have the same dimensions.
d. –2C
Answer:
\(\left[\begin{array}{ccc}
-10 & -4 & -18 \\
-12 & -2 & -6 \\
2 & -2 & 0
\end{array}\right]\)
e. 4D-2C
Answer:
\(\left[\begin{array}{ccc}
-6 & 20 & -18 \\
0 & -2 & 2 \\
6 & 10 & -8
\end{array}\right]\)
f. 3B-3B
Answer:
\(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
g. 5B-C
Answer:
Matrix C cannot be subtracted from 5B because they do not have the same dimensions.
h. B-3A
Answer:
\(\left[\begin{array}{cc}
-1 & -5 \\
-1 & 1
\end{array}\right]\)
i. C+10D
Answer:
\(\left[\begin{array}{ccc}
15 & 62 & 9 \\
36 & 1 & 23 \\
9 & 31 & -20
\end{array}\right]\)
j. \(\frac{1}{2}\)C+D
Answer:
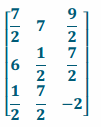
k. \(\frac{1}{4}\)B
Answer:
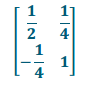
l. 3D-4A
Answer:
Matrix 4A cannot be subtracted from 3D because they do not have the same dimensions.
m. \(\frac{1}{3}\)B-\(\frac{2}{3}\)A
Answer:
\(\left[\begin{array}{cc}
0 & -1 \\
-\frac{1}{3} & \frac{2}{3}
\end{array}\right]\)
Question 2.
For the matrices given below, perform each of the following calculations, or explain why the calculation is not possible.
A=\(\left[\begin{array}{lll}
1 & 2 & 1 \\
3 & 0 & 2
\end{array}\right]\)
B=\(\left[\begin{array}{ll}
2 & 1 \\
3 & 6 \\
1 & 0
\end{array}\right]\)
C=\(\left[\begin{array}{ccc}
1 & -2 & 3 \\
1 & 1 & 4
\end{array}\right]\)
D=\(\left[\begin{array}{cc}
2 & -1 \\
-1 & 0 \\
4 & 1
\end{array}\right]\)
a. A+2B
Answer:
Matrices A and 2B cannot be added together because they do not have the same dimensions.
b. 2A-C
Answer:
\(\left[\begin{array}{ccc}
1 & 6 & -1 \\
5 & -1 & 0
\end{array}\right]\)
c. A+C
Answer:
\(\left[\begin{array}{lll}
2 & 0 & 4 \\
4 & 1 & 6
\end{array}\right]\)
d. -2C
Answer:
\(\left[\begin{array}{ccc}
-2 & 4 & -6 \\
-2 & -2 & -8
\end{array}\right]\)
e. 4D-2C
Answer:
Matrix 2C cannot be subtracted from 4D because the matrices do not have the same dimensions.
f. 3D-3D
Answer:
\(\left[\begin{array}{ll}
0 & 0 \\
0 & 0 \\
0 & 0
\end{array}\right]\)
g. 5B-D
Answer:
\(\left[\begin{array}{cc}
8 & 6 \\
16 & 30 \\
1 & -1
\end{array}\right]\)
h. C-3A
Answer:
\(\left[\begin{array}{ccc}
-2 & -8 & 0 \\
-8 & 1 & -2
\end{array}\right]\)
i. B+10D
Answer:
\(\left[\begin{array}{cc}
22 & -9 \\
-7 & 6 \\
41 & 10
\end{array}\right]\)
j. \(\frac{1}{2}\)C+A
Answer:
\(\left[\begin{array}{lll}
\frac{3}{2} & 1 & \frac{5}{2} \\
\frac{7}{2} & \frac{1}{2} & 4
\end{array}\right]\)
k. \(\frac{1}{4}\)B
Answer:
\(\left[\begin{array}{ll}
\frac{1}{2} & \frac{1}{4} \\
\frac{3}{4} & \frac{3}{2} \\
\frac{1}{4} & 0
\end{array}\right]\)
l. 3A+3B
Answer:
Matrices 3A and 3B cannot be added together because they do not have the same dimension.
m. \(\frac{1}{3}\)B-\(\frac{2}{3}\)D
Answer:
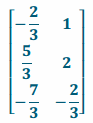
Question 3.
Let
A=\(\left[\begin{array}{cc}
3 & \frac{2}{3} \\
-1 & 5
\end{array}\right]\)
and
B=\(\left[\begin{array}{ll}
\frac{1}{2} & \frac{3}{2} \\
4 & 1
\end{array}\right]\)
a. Let C=6A+6B. Find matrix C.
Answer:
C=\(\left[\begin{array}{ll}
21 & 13 \\
18 & 36
\end{array}\right]\)
b. Let D=6(A+B). Find matrix D.
Answer:
D=\(\left[\begin{array}{ll}
21 & 13 \\
18 & 36
\end{array}\right]\)
c. What is the relationship between matrices C and D? Why do you think that is?
Answer:
The matrices are the same. Multiplying by a scalar appears to be distributive with matrices.
Question 4.
Let A=\(\left[\begin{array}{cc}
3 & 2 \\
-1 & 5 \\
3 & -4
\end{array}\right]\) and X be a 3×2 matrix. If A+X=\(\left[\begin{array}{cc}
-2 & 3 \\
4 & 1 \\
1 & -5
\end{array}\right]\), then find X.
Answer:
X = \(\left[\begin{array}{cc}
-5 & 1 \\
5 & -4 \\
-2 & -1
\end{array}\right]\)
Question 5.
Let A=\(\left[\begin{array}{lll}
1 & 3 & 2 \\
3 & 1 & 2 \\
4 & 3 & 2
\end{array}\right]\) and B=\(\left[\begin{array}{lll}
2 & 1 & 3 \\
2 & 2 & 1 \\
1 & 3 & 1
\end{array}\right]\) represent the bus routes of two companies between three cities.
a. Let C=A+B. Find matrix C. Explain what the resulting matrix and entry c1,3 mean in this context.
Answer:
C=\(\left[\begin{array}{lll}
3 & 4 & 5 \\
5 & 3 & 3 \\
5 & 6 & 3
\end{array}\right]\). Entry c1,3=5 means that there are 5 ways to get from city 1 to city 3 using either bus company.
b. Let D=B+A. Find matrix D. Explain what the resulting matrix and entry d1,3 mean in this context.
Answer:
D=\(\left[\begin{array}{lll}
3 & 4 & 5 \\
5 & 3 & 3 \\
5 & 6 & 3
\end{array}\right]\). Entry d1,3=5 means that there are 5 ways to get from city 1 to city 3 using either bus company.
c. What is the relationship between matrices C and D? Why do you think that is?
Answer:
Matrices C and D are equal. When we add two matrices, we add the real numbers in the corresponding spots. When two real numbers are added, the order doesn’t matter, so it makes sense that it doesn’t matter the order in which we add matrices.
Question 6.
Suppose that April’s Pet Supply has three stores in cities 1, 2, and 3. Ben’s Pet Mart has two stores in cities 1 and 2. Each shop sells the same type of dog crates in sizes 1 (small), 2 (medium), 3 (large), and 4 (extra large).
April’s and Ben’s inventory in each city is stored in the tables below.
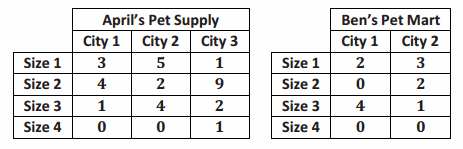
Create a matrix A so that ai,j represents the number of crates of size i available in April’s store in City j.
Answer:

b. Explain how the matrix 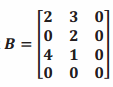 can represent the dog crate inventory at Ben’s Pet Mart.
can represent the dog crate inventory at Ben’s Pet Mart.
Answer:
The first two columns represent the inventory in Ben’s stores in cities 1 and 2. Since there is no store in city 3, Ben has no inventory of dog crates in this city, which is represented by the zeros in the third column of matrix B.
c. Suppose that April and Ben merge their inventories. Find a matrix that represents their combined inventory in each of the three cities.
Answer:
Matrix 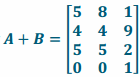 represents the combined inventory in each of the three cities. For example, since the entry in row 4, column 1 is 0, there are no extra large dog crates in either store in city 1. And, since the entry in row 1, column 2 is 8, there are a combined 8 small crates between the stores in city 2.
represents the combined inventory in each of the three cities. For example, since the entry in row 4, column 1 is 0, there are no extra large dog crates in either store in city 1. And, since the entry in row 1, column 2 is 8, there are a combined 8 small crates between the stores in city 2.
Question 7.
Jackie has two businesses she is considering buying and a business plan that could work for both. Consider the tables below, and answer the questions following.
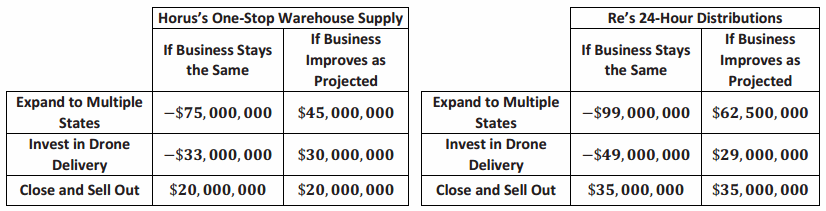
a. Create matrices H and R representing the values in the tables above such that the rows represent the different options and the columns represent the different outcomes of each option.
Answer:
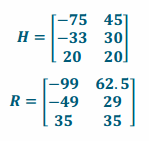
b. Calculate R-H. What does R-H represent?
Answer:
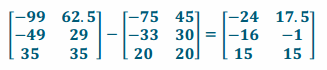
R-H represents how much more money Jackie makes buying the second business instead of the first in each situation. Note that negative values mean that Jackie loses more money with those choices.
c. Calculate H+R. What does H+R represent?
Answer:
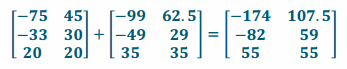
H+R represents what could happen if Jackie buys both businesses.
d. Jackie estimates that the economy could cause fluctuations in her numbers by as much as 5% both ways. Find matrices to represent the best and worst case scenarios for Jackie.
Answer:

e. Which business should Jackie buy? Which of the three options should she choose? Explain your choices.
Answer:
Answers may vary depending on how students feel about risk and income. There are two poor choices. If Jackie is planning to sell out the business she buys, then Re’s business results in a guaranteed increase of $15 million. Also, if Jackie is planning to invest in drones, then she should buy Horus’s business since it is both less risky and results in a greater return.
Eureka Math Precalculus Module 2 Lesson 2 Exit Ticket Answer Key
The diagram below represents a network of highways and railways between three cities. Highways are represented by black lines, and railways are represented by red lines.
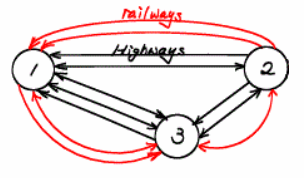
Question 1.
Create matrix A that represents the number of major highways connecting the three cities and matrix B that represents the number of railways connecting the three cities.
Answer:
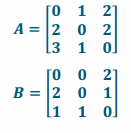
Question 2.
Calculate and interpret the meaning of each matrix in this situation
a. A+B
Answer:
A+B=\(\left[\begin{array}{lll}
0 & 1 & 4 \\
4 & 0 & 3 \\
4 & 2 & 0
\end{array}\right]\). The resulting matrix represents the numbers of ways that a person can travel between the three cities by taking any of the major highways or railways.
b. 3B
3B=\(\left[\begin{array}{lll}
0 & 0 & 6 \\
6 & 0 & 3 \\
3 & 3 & 0
\end{array}\right]\) The resulting matrix means the number of trains between the three cities has tripled.
Question 3.
Find A-B. Does the matrix A-B have any meaning in this situation? Explain your reasoning.
Answer:
A-B=\(\left[\begin{array}{lll}
0 & 1 & 0 \\
0 & 0 & 1 \\
2 & 0 & 0
\end{array}\right]\). The entries in matrix A-B represent how many more routes there are by highway than there are by train between two cities. For example, the 2 in the third row and first column indicates that there are two more ways to get from city 3 to city 1 by highway than there are by rail.