Eureka Math Precalculus Module 2 Lesson 19 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 19 Answer Key

Eureka Math Precalculus Module 2 Lesson 19 Example Answer Key

Example: The Parallelogram Rule for Vector Addition
When the initial point of a vector is the origin, then the coordinates of the terminal point will correspond to the horizontal and vertical components of the vector. This type of vector, with initial point at the origin, is often called a position vector.
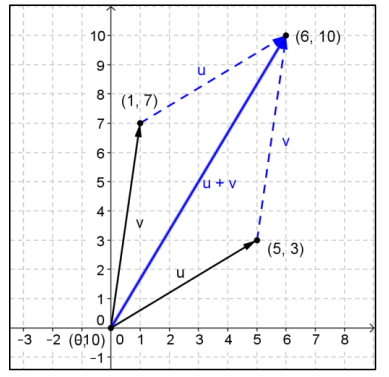
a. Draw arrows to represent the vectors v = 〈5, 3〉 and u = 〈1, 7〉 with the initial point of each vector at (0, 0).
b. Add v + u end – to – end. What is v + u? Draw the arrow that represents v + u with initial point at the origin.
c. Add u + v end – to – end. What is u + v? Draw the arrow that represents u + v with an initial point at the origin.

Answer:

Eureka Math Precalculus Module 2 Lesson 19 Exercise Answer Key

Exercises 1–7
Exercise 1.
Several vectors, represented by arrows, are shown below. For each vector, state the initial point, terminal point, component form of the vector and magnitude.

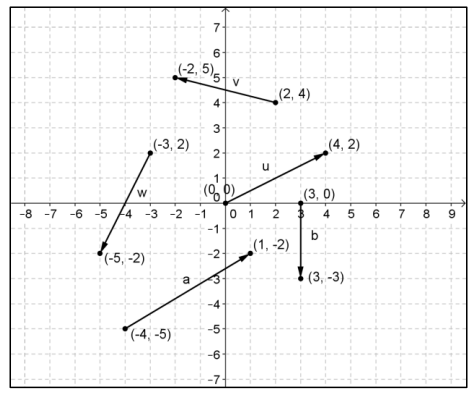
Answer:
For v,
Initial point (2, 4) and terminal point ( – 2, 5); v = 〈 – 4, 1〉 and ‖v‖ = \(\sqrt{17}\)
For u,
Initial point (0, 0) and terminal point (4, 2); u = 〈4, 2〉 and ‖u‖ = \(\sqrt{20}\) = 2\(\sqrt{5}\)
For w,
Initial point ( – 3, 2) and terminal point ( – 5, – 2); w = 〈 – 2, – 4〉 and ‖w‖ = \(\sqrt{20}\) = 2\(\sqrt{5}\)
For a,
Initial point ( – 4, – 5) and terminal point (1, – 2); a = 〈5, 3〉 and ‖a‖ = \(\sqrt{34}\)
For b,
Initial point (3, 0) and terminal point (3, – 3); b = 〈0, – 3〉 and ‖b‖ = 3

Exercise 2.
Several vectors, represented by arrows, are shown below. For each vector, state the initial point, terminal point, component form of the vector, and magnitude.

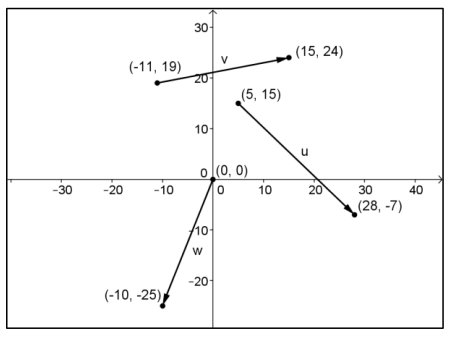
Answer:
For v,
Initial point ( – 11, 19) and terminal point (15, 24); v = 〈26, 5〉 and ‖v‖ = \(\sqrt{701}\)
For u,
Initial point (5, 15) and terminal point (28, – 7); u = 〈23, – 22〉 and ‖u‖ = \(\sqrt{1013}\)
For w,
Initial point (0, 0) and terminal point ( – 10, – 25); w = 〈 – 10, – 25〉 and ‖w‖ = \(\sqrt{725}\)

Exercise 3.
Write a rule for the component form of the vector v shown in the diagram. Explain how you got your answer.

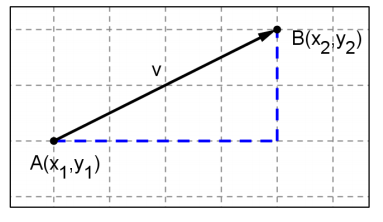
Answer:
The component form is v = 〈x₂ – x₁, y₂ – y₁〉. The components of the vector are the distance A is translated vertically and horizontally to get to B. To find the horizontal distance from A to B, subtract the x – coordinates. To find the vertical distance from A to B, subtract the y – coordinates.

When we use the initial and terminal points to describe a vector, we often refer to the vector as a directed line segment. A vector or directed line segment with initial point A and terminal point B is denoted \(\overrightarrow{A B}\).

Exercise 4.
Write each vector in component form.

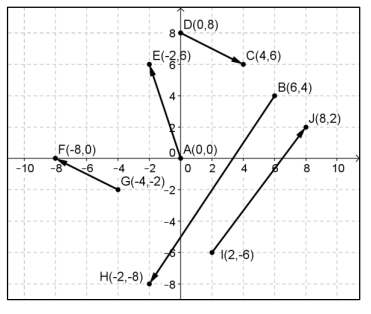
a. \(\overrightarrow{A E}\)
Answer:
\(\overrightarrow{A E}\) = 〈 – 2, 6〉

b. \(\overrightarrow{B H}\)
Answer:
\(\overrightarrow{B H}\) = 〈 – 8, – 12〉

c. \(\overrightarrow{D C}\)
Answer:
\(\overrightarrow{D C}\) = 〈4, – 2〉

d. \(\overrightarrow{G F}\)
Answer:
\(\overrightarrow{G F}\) = 〈 – 4, 2〉

e. \(\overrightarrow{I J}\)
Answer:
\(\overrightarrow{I J}\) = 〈6, 8〉

Exercise 5.
Consider points P(2, 1), Q( – 3, 3), and R(1, 4).
a. Compute \(\overrightarrow{P Q}\) and \(\overrightarrow{Q P}\) and show that \(\overrightarrow{P Q}\) + \(\overrightarrow{Q P}\) is the zero vector. Draw a diagram to show why this makes sense geometrically.
Answer:

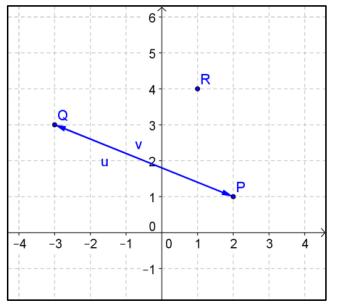
\(\overrightarrow{P Q}\) = 〈 – 5, 2〉 and \(\overrightarrow{Q P}\) = 〈5, – 2〉
\(\overrightarrow{P Q}\) + \(\overrightarrow{Q P}\) = 〈 – 5 + 5, 2 – 2〉 = 〈0, 0〉
This makes sense because one vector translates P to Q, and then the other vector translates the point back from Q to P. The sum would be the zero vector because the original point is returned to its starting location.

b. Plot the points P, Q, and R. Use the diagram to explain why \(\overrightarrow{P Q}\) + \(\overrightarrow{Q R}\) + \(\overrightarrow{R P}\) is the zero vector. Show that this is true by computing the sum \(\overrightarrow{P Q}\) + \(\overrightarrow{Q R}\) + \(\overrightarrow{R P}\).
Answer:

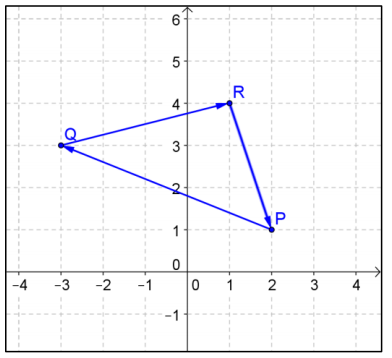
The diagram shows that the sum should be the zero vector because point P is translated back to its original coordinates when you add the three vectors.
\(\overrightarrow{P Q}\) + \(\overrightarrow{Q R}\) + \(\overrightarrow{R P}\) = 〈 – 5 + 4 + 1, 2 + 1 – 3〉 = 〈0, 0〉

Exercise 6.
Show for any two points A and B that – \(\overrightarrow{A B}\) = \(\overrightarrow{B A}\).
Answer:
Consider A(x₁, y₁ ) and B(x₂, y₂ ). Then \(\overrightarrow{A B}\) = 〈x₂ – x₁, y₂ – y₂ 〉
and – \(\overrightarrow{A B}\) = 〈 – x₂ + x₁, – y₂ + y₂ 〉 = 〈x₁ – x₂, y₁ – y₂ 〉.
This is the component form of \(\overrightarrow{B A}\) = 〈x₁ – x₂, y₁ – y₂ 〉.

Exercise 7.
Given the vectors v = 〈2, – 3〉, w = 〈 – 5, 1〉, u = 〈4, – 2〉, and t = 〈 – 1, 4〉.
a. Verify that the sum of these four vectors is the zero vector.
Answer:
v + w = 〈 – 3, – 2〉 and v + w + u = 〈1, – 4〉 and v + w + u + t = 〈0, 0〉

b. Draw a diagram representing the vectors as arrows placed end – to – end to support why their sum would be the zero vector.
Answer:

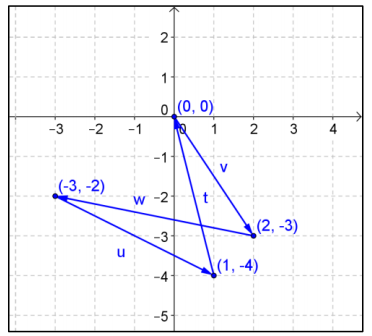
If we position v to have an initial point at (0, 0) then v translates the point (0, 0) to (2, – 3). Each additional vector translates the point by its components. The result of all four translations returns the point back to the origin.

Exercises 8–10
Let u = 〈 – 2, 5〉 and v = 〈4, 3〉.
a. Draw a diagram to illustrate v and u, and then find v + u using the parallelogram rule.
Answer:

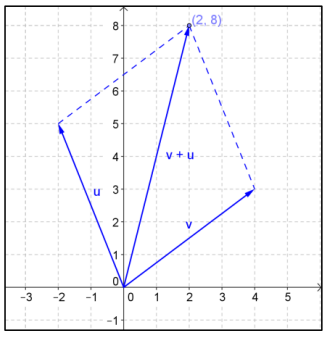
v + u = 〈2, 8〉

b. Draw a diagram to illustrate 2v, and then find 2v + u using the parallelogram rule.
Answer:

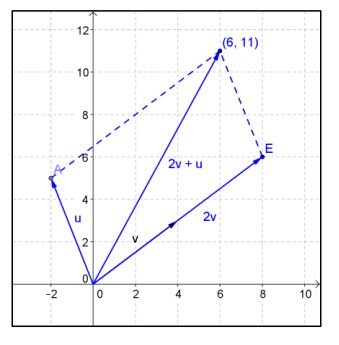
2v + u = 〈6, 11〉

c. Draw a diagram to illustrate – v, and then find u – v using the parallelogram rule.
Answer:

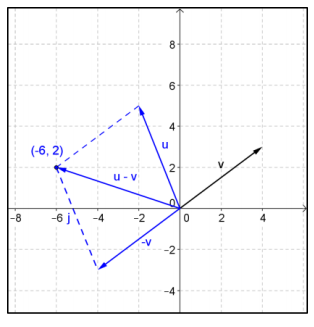
u – v = 〈 – 6, 2〉

d. Draw a diagram to illustrate 3v and – 3v.
Answer:

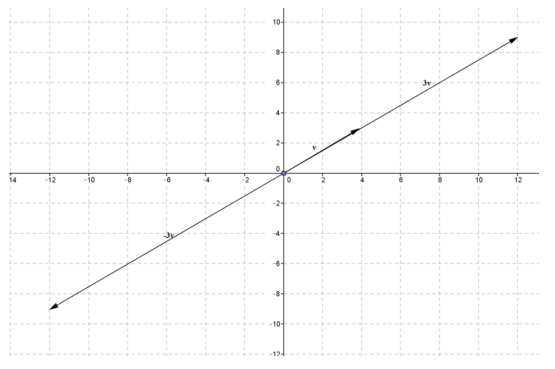
i. How do the magnitudes of these vectors compare to one another and to that of v?
Answer:
The magnitude of 3v and – 3v are the same. The magnitude of these vectors is 3 times the magnitude of v. You can see that because scalar multiplication dilates the vector by the scalar multiple.

ii. How do the directions of 3v and – 3v compare to the direction of v?
Answer:
When the scalar is positive, the direction of the scalar multiple is the same going along v. When the scalar is negative, the direction is opposite the direction of v.

Directed line segments can also be represented in ℝ³. Instead of two coordinates like we use in ℝ², we simply use three to locate a point in space relative to the origin, denoted (0, 0, 0). Thus, the vector \(\overrightarrow{A B}\) with initial point A(x₁, y₁, z₁) and terminal point B(x₂, y₂, z₂ ) would have component form:
\(\overrightarrow{A B}\) = 〈x₂ – x₁, y₂ – y₁, z₂ – z₁ 〉.
Consider points A(1, 0, – 5) and B(2, – 3, 6).
a. What is the component form of \(\overrightarrow{A B}\)?
Answer:
\(\overrightarrow{A B}\) = 〈2 – 1, – 3 – 0, 6 – ( – 5)〉 = 〈1, – 3, 11〉

b. What is the magnitude of \(\overrightarrow{A B}\)?
Answer:
‖\(\overrightarrow{A B}\)‖ = \(\sqrt{1^{2} + ( – 3)^{2} + 11^{2}}\) = \(\sqrt{131}\)

Exercise 10.
Consider points A(1, 0, – 5), B(2, – 3, 6), and C(3, 1, – 2).
a. Show that \(\overrightarrow{A B}\) + \(\overrightarrow{B A}\) = 0. Explain your answer using geometric reasoning.
Answer:
\(\overrightarrow{A B}\) = 〈1, – 3, 11〉 and \(\overrightarrow{B A}\) = 〈 – 1, 3, – 11〉
\(\overrightarrow{A B}\) + \(\overrightarrow{B A}\) = 〈1 – 1, – 3 + 3, 11 – 11〉 = 〈0, 0, 0〉
\(\overrightarrow{A B}\) translates A to B and \(\overrightarrow{B A}\) translates B back to A. The net translation effect is zero.

b. Show that \(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) + \(\overrightarrow{C A}\) = 0. Explain your answer using geometric reasoning.
Answer:
We have \(\overrightarrow{A B}\) = 〈1, – 3, 11〉, \(\overrightarrow{B C}\) = 〈1, 4, – 8〉, and \(\overrightarrow{C A}\) = 〈 – 2, – 1, – 3〉.
Adding all the respective components together gives
\(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) + \(\overrightarrow{C A}\) = 〈1 + 1 – 2, – 3 + 4 – 1, 11 – 8 – 3〉 = 〈0, 0, 0〉.
The sum of these three vectors translates A to B, then B to C and then C to A. The net translation effect is zero.

Eureka Math Precalculus Module 2 Lesson 19 Problem Set Answer Key

Question 1.
Vectors u, v, w, a, and b are shown at right.

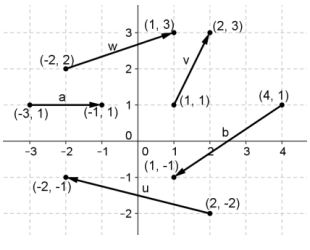
a. Find the component form of u, v, w, a, and b.
Answer:
u = 〈 – 4, 1〉, v = 〈1, 2〉, w = 〈3, 1〉, a = 〈2, 0〉, b = 〈 – 3, – 2〉

b. Find the magnitudes‖u‖, ‖v‖, ‖w‖, ‖a‖, and‖b‖.
Answer:
‖u‖ = \(\sqrt{17}\), ‖v‖ = \(\sqrt{5}\), ‖w‖ = \(\sqrt{10}\), ‖a‖ = 2, ‖b‖ = \(\sqrt{13}\)

c. Find the component form of u + v and calculate‖u + v‖.
Answer:
〈 – 3, 3〉, ‖u + v‖ = 3\(\sqrt{2}\)

d. Find the component form of w – b and calculate‖w – b‖.
Answer:
〈6, 3〉, ‖w – b‖ = 3\(\sqrt{5}\)

e. Find the component form of 3u – 2v.
Answer:
〈 – 14, – 1〉

f. Find the component form of v – 2(u + b).
Answer:
〈15, 4〉

g. Find the component form of 2(u – 3v) – a.
Answer:
〈 – 16, – 10〉

h. Find the component form of u + v + w + a + b.
Answer:
〈 – 1, 2〉

i. Find the component form of u – v – w – a + b.
Answer:
〈 – 13, – 4〉

j. Find the component form of 2(u + 4v) – 3(w – 3a + 2b).
Answer:
〈27, 27〉

Question 2.
Given points A(1, 2, 3), B( – 3, 2, – 4), C( – 2, 1, 5), find component forms of the following vectors.
a. \(\overrightarrow{A B}\) and \(\overrightarrow{B A}\)
Answer:
\(\overrightarrow{A B}\) = 〈 – 4, 0, – 7〉, \(\overrightarrow{B A}\) = 〈4, 0, 7〉

b. \(\overrightarrow{B C}\) and \(\overrightarrow{C B}\)
Answer:
\(\overrightarrow{B C}\) = 〈1, – 1, 9〉, \(\overrightarrow{C B}\) = 〈 – 1, 1, – 9〉

c. \(\overrightarrow{C A}\) and \(\overrightarrow{A C}\)
Answer:
\(\overrightarrow{C A}\) = 〈3, 1, – 2〉, \(\overrightarrow{A C}\) = 〈 – 3, – 1, 2〉

d. \(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) – \(\overrightarrow{A C}\)
Answer:
〈0, 0, 0〉

e. – \(\overrightarrow{B C}\) + \(\overrightarrow{B A}\) + \(\overrightarrow{A C}\)
Answer:
〈0, 0, 0〉

f. \(\overrightarrow{A B}\) – \(\overrightarrow{C B}\) + \(\overrightarrow{C A}\)
Answer:
〈0, 0, 0〉

Question 3.
Given points A(1, 2, 3), B( – 3, 2, – 4), C( – 2, 1, 5), find the following magnitudes.
a.‖\(\overrightarrow{A B}\)‖
Answer:
‖\(\overrightarrow{A B}\)‖ = \(\sqrt{65}\)

b.‖\(\overrightarrow{A B}\) + \(\overrightarrow{B C}\)‖.
Answer:
‖\(\overrightarrow{A B}\) + \(\overrightarrow{B C}\)‖ = \(\sqrt{14}\)

c.‖\(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) + \(\overrightarrow{C A}\)‖
Answer:
0

Question 4.
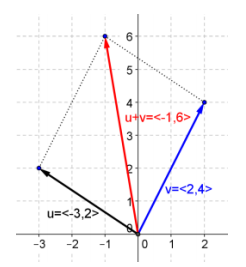
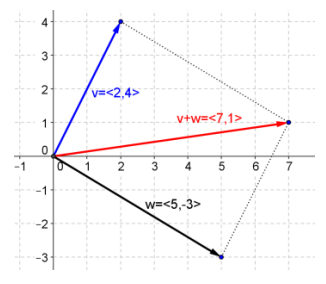
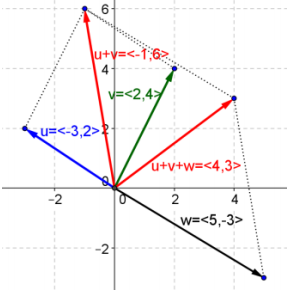
Given vectors u = 〈 – 3, 2〉, v = 〈2, 4〉, w = 〈5, – 3〉, use the parallelogram rule to graph the following vectors.
a. u + v
Answer:

b. v + w
Answer:

c. u – v
Answer:

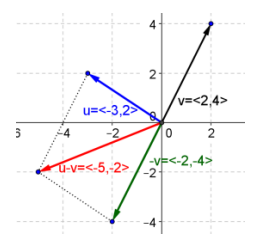
d. v – w
Answer:

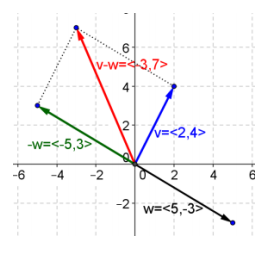
e. 2w + v
Answer:

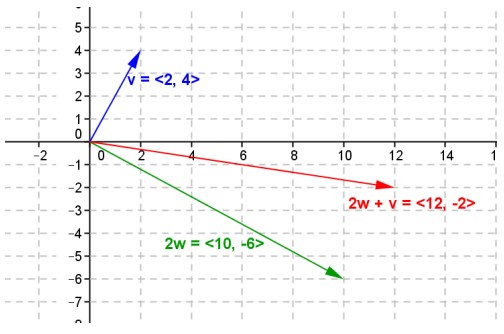
f. 3u – 2v
Answer:

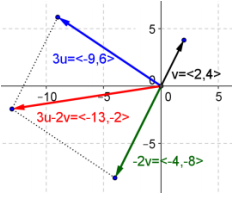
g. u + v + w
Answer:

Question 5.
Points A, B, C, D, E, F, G, and H and vectors u, v, and w are shown below. Find the components of the following vectors.

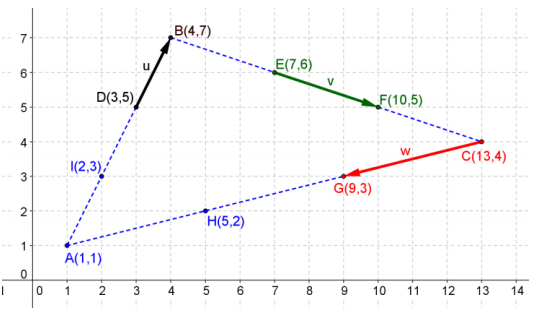
Answer:
a. \(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) + \(\overrightarrow{C A}\)
Answer:
\(\overrightarrow{A B}\) = 〈3, 6〉, \(\overrightarrow{B C}\) = 〈9, – 3〉, \(\overrightarrow{C A}\) = 〈 – 12, – 3〉, \(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) + \(\overrightarrow{C A}\) = 0

b. u + v + w
Answer:
u = 〈1, 2〉, v = 〈3, – 1〉, w = 〈 – 4, – 1〉, u + v + w = 0

c. \(\overrightarrow{A D}\) + \(\overrightarrow{B E}\) + \(\overrightarrow{C G}\)
Answer:
\(\overrightarrow{A D}\) = 〈2, 4〉, \(\overrightarrow{B E}\) = 〈3, – 1〉, \(\overrightarrow{C G}\) = 〈 – 4, – 1〉, \(\overrightarrow{A B}\) + \(\overrightarrow{B C}\) + \(\overrightarrow{C A}\) = 〈1, 2〉

Question 6.
Consider Example 5, part (b) in the lesson and Problem 5, part (a) above. What can you conclude about three vectors that form a triangle when placed tip – to – tail? Explain by graphing.
Answer:

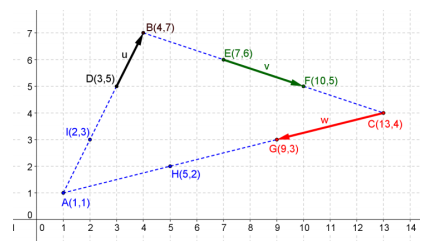
If three vectors form a triangle when placed tip – to – tail, then the sum of those three vectors is zero.

Question 7.
Consider the vectors shown below.

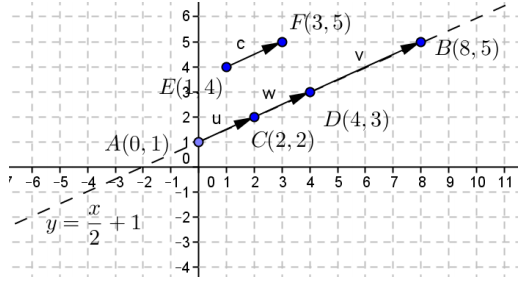
a. Find the components of vectors u = \(\overrightarrow{A C}\), w = \(\overrightarrow{A D}\), v = \(\overrightarrow{A B}\), and c = \(\overrightarrow{E F}\).
Answer:
u = \(\overrightarrow{A C}\) = 〈2, 1〉, w = \(\overrightarrow{A D}\) = 〈4, 2〉, v = \(\overrightarrow{A B}\) = 〈8, 4〉, c = \(\overrightarrow{E F}\) = 〈2, 1〉

b. Is vector u equal to vector c?
Answer:
Yes, u = 〈2, 1〉 = c, they have the same components and direction.

c. Jens says that if two vectors u and v have the same initial point A and lie on the same line, then one vector is a scalar multiple of the other. Do you agree with him? Explain how you know. Give an example to support your answer.
Answer:
Yes. Suppose that the terminal point of u is C and the terminal point of v is B. Then u has magnitude ‖AC‖, where ‖AC‖ ≠ 0, and v has magnitude ‖AB‖, where‖AB‖≠0. If u and v point in the same direction, then v = \(\left(\frac{\| A B}{\|A C\|}\right) \mathrm{u}\). If u and v point in opposite directions, then v = – \(\left(\frac{\| A B}{\|A C\|}\right) \mathrm{u}\). For example in the diagram above, vector u = \(\overrightarrow{A C}\) = 〈2, 1〉 and vector v = \(\overrightarrow{A B}\) = 〈8, 4〉, and we have v = \(\frac{\sqrt{80}}{\sqrt{5}} \mathrm{u}\) = 4u.

Eureka Math Precalculus Module 2 Lesson 19 Exit Ticket Answer Key

Question 1.
Consider vectors with their initial and terminal points as shown below. Find the components of the specified vectors and their magnitudes.

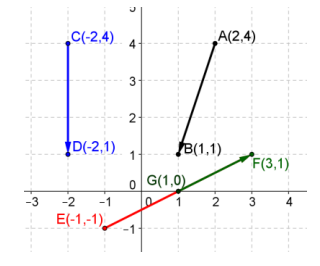
a. u = \(\overrightarrow{E F}\) and ‖u‖
Answer:
u = 〈4, 2〉, ‖u‖ = 2\(\sqrt{5}\)

b. v = \(\overrightarrow{A B}\) and ‖v‖
Answer:
v = 〈 – 1, – 3〉, ‖v‖ = \(\sqrt{10}\)

c. w = \(\overrightarrow{C D}\) and ‖w‖
Answer:
w = 〈0, – 3〉, ‖w‖ = 3

d. t = \(\overrightarrow{G F}\) and ‖t‖
Answer:
t = 〈2, 1〉, ‖t‖ = \(\sqrt{5}\)

Question 2.
For vectors u and v as in Question 1, explain how to find u + v using the parallelogram rule. Support your answer graphically below.

Answer:

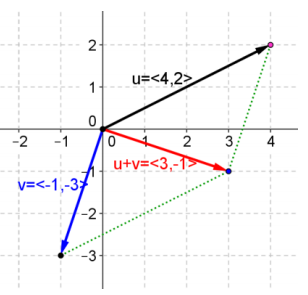
To find u + v using the parallelogram rule, form a parallelogram with vectors u and v as sides. The diagonal of the parallelogram is the sum of the two vectors.