Eureka Math Precalculus Module 2 Lesson 18 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 18 Answer Key

Eureka Math Precalculus Module 2 Lesson 18 Opening Exercise Answer Key

Opening Exercise:

Write each vector described below in component form and find its magnitude. Draw an arrow originating from (0, 0) to represent each vector’s magnitude and direction.

Answer:

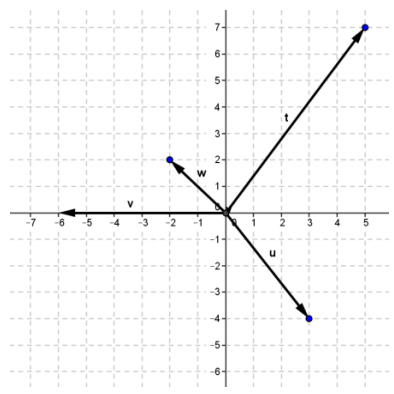
a. Translate 3 units right and 4 units down.
Answer:
u = (3, -4), ||u|| = 5

b. Translate 6 units left.
Answer:
v = (-6, 0), ||v|| = 6

c. Translate 2 units left and 2 units up.
Answer:
w = (-2, 2), ||w||= 2√2

d. Translate 5 units right and 7 units up.
Answer:
t = (5, 7), ||t|| = \(\sqrt{25+49}\) = √74

Eureka Math Precalculus Module 2 Lesson 18 Exercise Answer Key

Exercises 1 – 3:

Exercise 1.
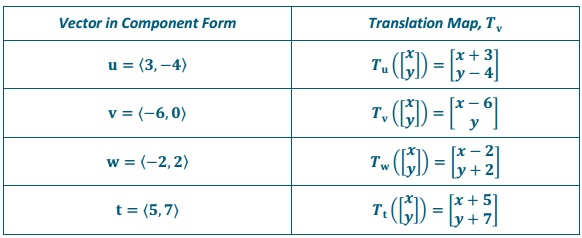
Write a translation map defined by each vector from the opening.
Consider the vector v = (-2, 5) and its associated translation map:
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left(\begin{array}{l}
x-2 \\
y+5
\end{array}\right)\)
Answer:

Exercise 2.
Suppose we apply the translation map T_v to each point on the circle (x + 4)² + (y – 3)² = 25.

a. What is the radius and center of the original circle?
Answer:
The radius is 5 and the center is (-4, 3).

b. Show that the image points satisfy the equation of another circle.
Answer:
Suppose that T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]\). Then x = x – 2 and y = y + 5, so x = x’ + 2 and y = y’ – 5.
Since (x + 4)² + (y – 3)² = 25, we have
(x + 4)² + (y – 3)² = 25
((x’ + 2) +4)²+((y’ – 5) – 3)² = 25
(x’ + 6)² + (y’ – 8)² = 25
So, the image points \(\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]\) lie on a circle.

so the image points \(\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]\) lie on a circle.

c. What are the center and radius of this image circle?
Answer:

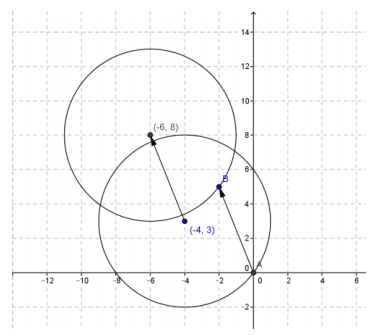
The radius of 5 remains unchanged. The new center is (-6, 8).

Exercise 3.
Suppose we apply the translation map T_v, to each point on the line 2x – 3y = 10.

a. What are the slope and y-intercept of the original line?
Answer:
The slope is \(\frac{2}{3}\) and the y-intercept is (0, –\(\frac{10}{3}\)).

b. Show that the image points satisfy the equation of another line.
Answer:
Suppose that T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x^{\prime} \\
y^{\prime}
\end{array}\right]]\). Then \(x^{\prime}\) = x – 2 and \(y^{\prime}\) = y + 5. so x = \(x^{\prime}\) + 2 and y = \(y^{\prime}\) – 5.
Since 2x – 3y = 10, we have
2(\(x^{\prime}\) + 2) – 3(\(y^{\prime}\) – 5) = 10
2\(x^{\prime}\) + 4 – 3\(y^{\prime}\) + 15 = 10
2\(x^{\prime}\) – 3\(y^{\prime}\) = -9

c. What are the slope and y-intercept of this image line?
Answer:

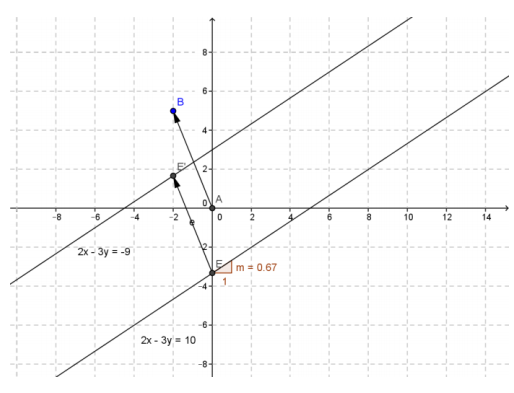
The slope is \(\frac{2}{3}\) and the y-intercept is (0, 3)

Example 1: Vectors and Translation Maps in R³

Translate by the vector v = (1, 3, 5) by applying the translation map T_v to the following objects in R³. A sketch of the original object and the vector is shown. Sketch the image.

\(T_{\mathrm{v}}\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x+1 \\
y+3 \\
z+5
\end{array}\right]\)

a. The point A(2, -2, 4)

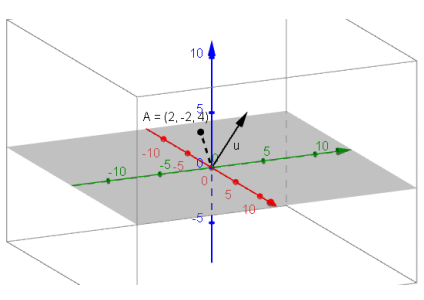
Answer:

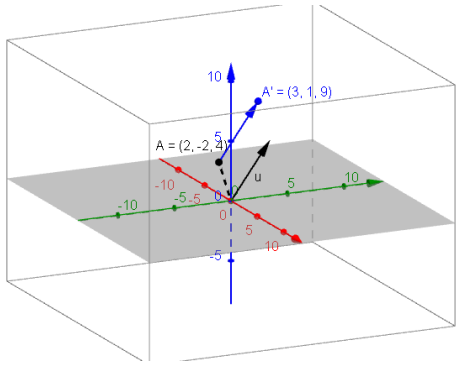
The new point will be (2 + 1, -2 + 3, 4 + 5) or (3, 1, 9).

b. The plane 2x + 3y – z = 0

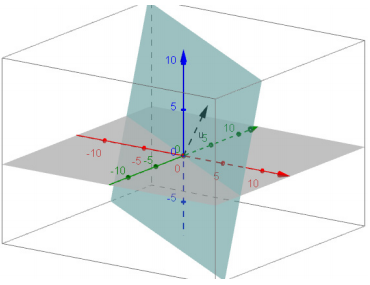
Answer:

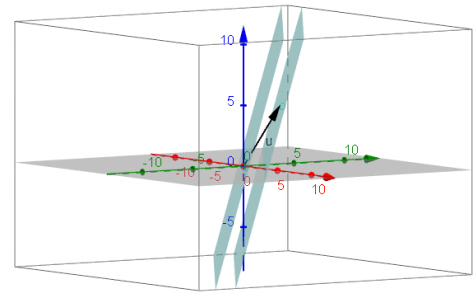
The new plane will be 2(x – 1) + 3(y – 3) – (z – 5) = 0, which ius equivalent to 2x + 3y – z = 6.

c. The sphere (x – 1)² + (y – 3)² + z² = 9.

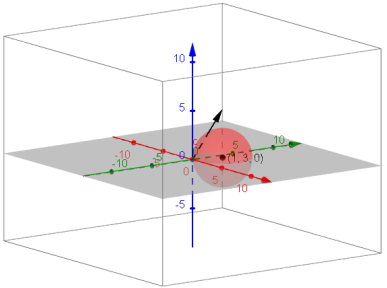
Answer:

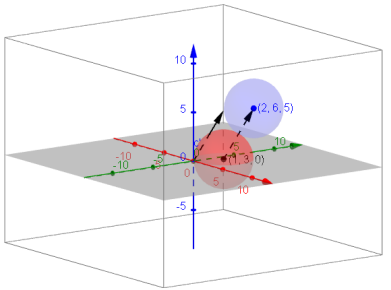
Exercise 4:
Given the sphere (x + 3)² + (y – 1)² + (z – 3)² = 10.

a. What are its center and radius?
Answer:
The center is (-3, 1, 3), and the radius is √10.

b. Write a vector and its associated translation map that would take this sphere to its image centered at the origin.
Answer:
We need to translate the center from the point (-3, 1, 3) to the point (0, 0, 0). This represents a translation of 3 units in the x direction, -1 unit in the y direction, and -3 units in the z direction. The vector is v = (3, -1, -3), and the translation map would be

T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x+3 \\
y-1 \\
z-3
\end{array}\right]\).

Example 2: What is the Magnitude of a Vector in R³?

a. Find a general formula for ||v||².
Answer:
||v||² = x² + y² + z²

b. Solve this equation for lvii to find the magnitude of the vector.
Answer:
||v|| = \(\sqrt{x^{2}+y^{2}+z^{2}}\)

Exercises 5 – 8:

Exercise 5.
Which vector has greater magnitude, y = (0, 5, -4) or u (3, -4, 4)? Show work to support your answer.
Answer:
||v|| = \(\sqrt{0^{2}+5^{2}+(-4)^{2}}=\sqrt{41}\)
||u|| = \(\sqrt{3^{2}+(-4)^{2}+4^{2}}=\sqrt{41}\)
These vectors have equal magnitude.

Exercise 6.
Explain why vectors can have equal magnitude but not be the same vector.
Answer:
A vector has both a magnitude and a direction. If you graphed the vectors from Exercise 5, you can see the point in different directions so they cannot be the same even though they have equal magnitude.

Exercise 7.
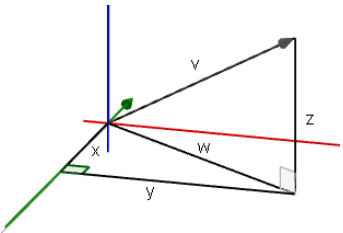
Vector arithmetic in R³ is analogous to vector arithmetic in R². Complete the graphic organizer to illustrate these ideas.

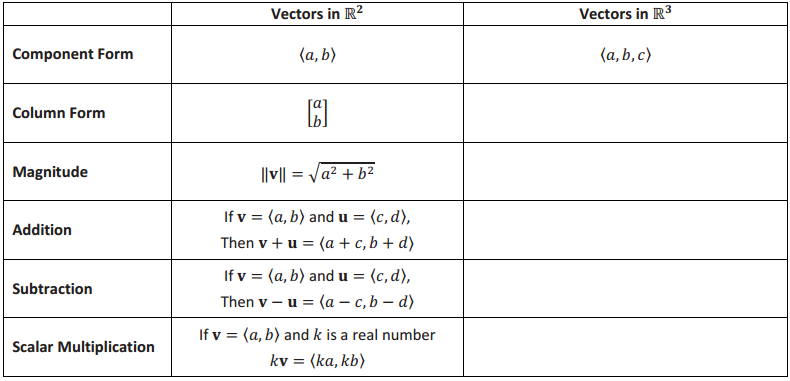
Answer:

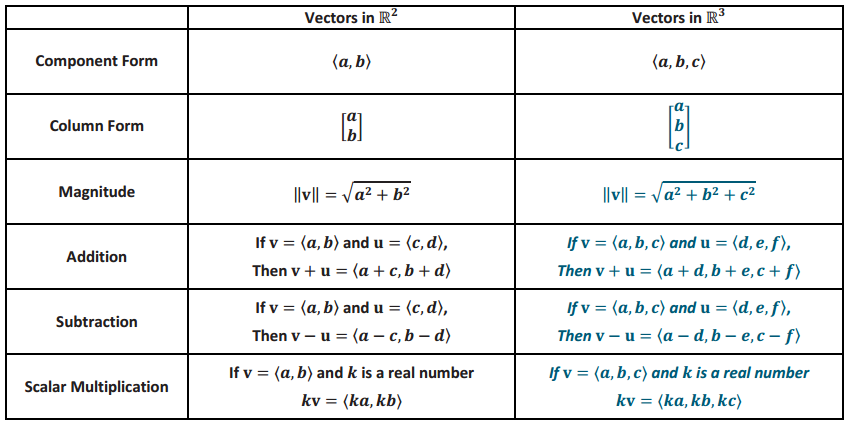
Exercise 8.
Given y = (2 ,0, -4) and u = (-1, 5, 3).

a. Calculate the following.

i. v + u
Answer:
v + u = (2 + (-1), 0 + 5, -4 + 3) = (1, 5,-1)

ii. 2v – u
Answer:
2v – u = (2 . 2 -(-1), 2 . 0 – 5, 2 (-4) – 3) = (5, -5, -11)

iii. ||u||
Answer:
||u|| = \(\sqrt{(-1)^{2}+5^{2}+3^{2}}=\sqrt{35}\)

b. Suppose the point (1, 3, 5) is translated by y and then by u. Determine a vector w that would return the point back to its original location (1, 3, 5).
Answer:
From part (a), we have v + u = (1, 5, -1). The point will be translated from (1, 3, 5) to (2, 8, 4) since 1 + 1 = 2, 5 + 3 = 8, and 5 – 1 = 4. The vector that will return this point to its original location will be the opposite of v + u.

-(v + u) = (-1,-5, 1)
And this vector will translate (2, 8, 4) back to (1, 3, 5) because 2 – 1 = 1, 8 – 5 = 3, and 4 + 1 = 5.

Eureka Math Precalculus Module 2 Lesson 18 Problem Set Answer Key

Question 1.
Myishia says that when applying the translation map T_v,\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+1 \\
y-2
\end{array}\right]\) to a set of points given by an equation relating x and y, we should replace every x that is in the equation by x + 1, and y by y – 2. For example, the equation of the parabola y = x² would become y – 2 = (x + 1)2. Is she correct? Explain your answer.
Answer:
No, she is not correct. What she did translates the points on the parabola y = x² in the opposite direction – one unit to the left and 2 units upward, which is not the geometric effect of T_v \(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+1 \\
y-2
\end{array}\right]\). In order to have the correct translation based on T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+1 \\
y-2
\end{array}\right]\), we need to set \(\boldsymbol{x}^{\prime}\) = x + 1 and \(\boldsymbol{y}^{\prime}\) = y – 2, which is equivalent to x = \(\boldsymbol{x}^{\prime}\) – 1 and y = \(\boldsymbol{y}^{\prime}\) + 2.
This process gives the transformed equation \(\boldsymbol{y}^{\prime}\) + 2 = (\(\boldsymbol{x}^{\prime}\) – 1)², which we write as y + 2 (x – 1)².

Question 2.
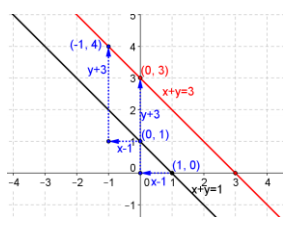
Given the vector y = (-1, 3), find the image of the line x + y = 1 under the translation map T_v. Graph the original line and its image, and explain the geometric effect of the map T, on the line.
Answer:

T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x-1 \\
y+3
\end{array}\right]\), x – (-1)) + (y – (3)) = 1, x + 1 + y – 3 = 1, x + y = 3
Every point on the line is shifted one unit left and three units upward. The slopes of the lines remain -1.

Question 3.
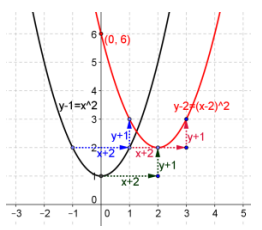
Given the vector v = (2, 1), find the image of the parabola y – 1 = x² under the translation map T_v. Draw a graph of the original parabola and its image, and explain the geometric effect of the map T_v on the parabola. Find the vertex and x-intercepts of the graph of the image.
Answer:

T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+2 \\
y+1
\end{array}\right]\), y – 2 = (x – 2)²

Every point on the parabola is shifted two units to the right and one unit upward. The vertex is (2, 2), and there are no x-intercepts.

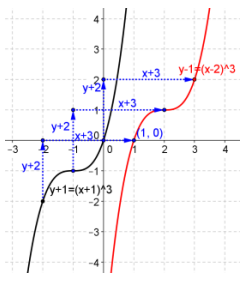
Question 4.
Given the vector y = (3, 2), find the image of the graph of y + 1 = (x + 1)³ under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the x-intercepts of the graph of the image.
Answer:

T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+3 \\
y+2
\end{array}\right]\), y – 1 = (x – 2)³
Every point on the curve is shifted three units to the right and two units upward. The x-intercept is 1.𝟏

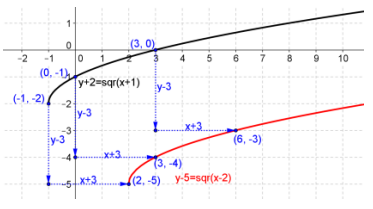
Question 5.
Given the vector y = (3, -3), find the image of the graph of y + 2 = \(\sqrt{x+1}\) under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the x-intercepts of the graph of the image.
Answer:

T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+3 \\
y-3
\end{array}\right]\), y + 5 = \(\sqrt{x-2}\)
Every point on the curve is shifted three units to the right and three units downward. The x-intercept is 27.

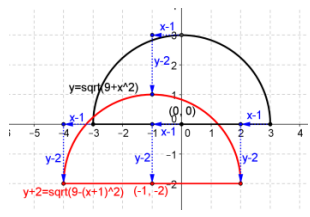
Question 6.
Given the vector y = (-1, -2), find the image of the graph of y = \(\sqrt{9-x^{2}}\) under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the x-intercepts of the graph of the image.
Answer:

T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x-1 \\
y-2
\end{array}\right]\), y + 2 = \(\sqrt{9-(x+1)^{2}}\)
Every point on the semicircle is shifted one unit to the left and two units downward.
x-intercepts: -1 + √5 and -1 – √5.

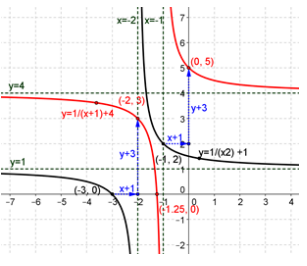
Question 7.
Given the vector y = (1, 3), find the image of the graph of y = \(\frac{1}{x+2}\) + 1 under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the equations of the asymptotes of the graph of the image.
Answer:

T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+1 \\
y+3
\end{array}\right]\), y = \(\frac{1}{x+1}\) + 4.
Every point on the curve is shifted one unit to the right and three units upward. The new vertical asymptote is x = -1, the new horizontal asymptote is y = 4.

Question 8.
Given the vector y = (-1, 2), find the image of the graph of y = |x + 2| + 1 under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the x-intercepts of the graph of the image.
Answer:

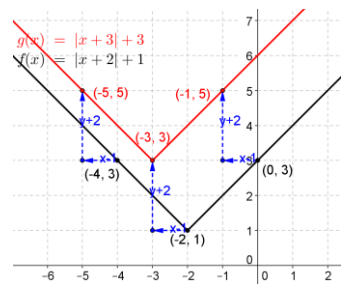
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x-1 \\
y+2
\end{array}\right]\)
Every point on the graph is shifted one unit to the left and two units upward. There are no x-intercepts.

Question 9.
Given the vector y = (1, -2), find the image of the graph of y = 2’ under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the x-intercepts of the graph of the image.
Answer:

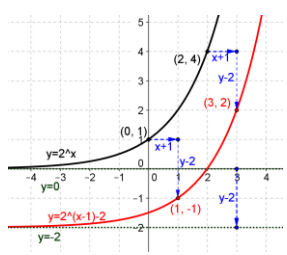
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+1 \\
y-2
\end{array}\right]\), y = 2^{x – 1} – 2
Every point on the curve is shifted one unit to the right and two units downward. x-intercept is 2.

Question 10.
Given the vector y = (-1, 3), find the image of the graph of y = log₂x, under the translation map T_v. Draw the original graph and its image, and explain the geometric effect of the map T_v, on the graph. Find the x-intercepts of the graph of the image.
Answer:

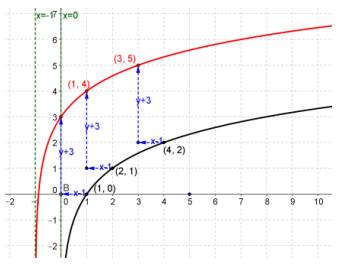
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x-1 \\
y+3
\end{array}\right]\), y = log₂(x + 1) + 3

Every point on the curve is shifted one unit to the left and three units upward. x-intercept: –\(\frac{7}{8}\)

Question 11.
Given the vector v =(2, -3), find the image of the graph of \(\frac{x^{2}}{4}+\frac{y^{2}}{16}\) = 1 under the transiatlon map T,. Draw the original graph and its image, and explain the geometric effect of the map T_v on the graph. Find the new center, major and minor axis of the graph of the image.
Answer:

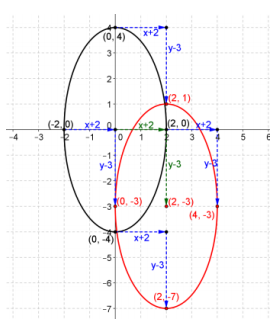
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+2 \\
y-3
\end{array}\right]\), \(\frac{(x-2)^{2}}{4}+\frac{(y+3)^{2}}{16}\) = 1

Every point on the ellipse is shifted two units to the right and three units downward. The new center is (2, -3), the major axis is 4, and the minor axis is 2.

Question 12.
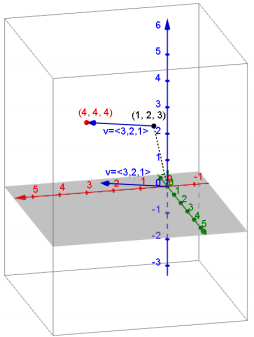
Given the vector v, find the image of the given point P under the translation map T_v. Graph P and its image.

a. v = (3, 2, 1), P = \(\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\)
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x+3 \\
y+2 \\
z+1
\end{array}\right]\), the new image: \(\left[\begin{array}{l}
4 \\
4 \\
4
\end{array}\right]\)

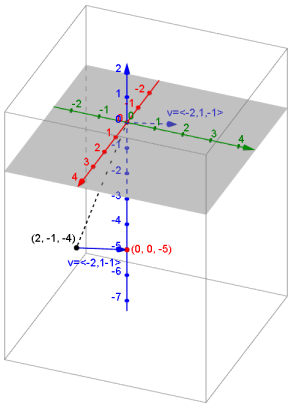
b. v = (-2, 1, -1), P = \(\left[\begin{array}{c}
2 \\
-1 \\
-4
\end{array}\right]\)
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x-2 \\
y+1 \\
z-1
\end{array}\right]\), the new image: \(\left[\begin{array}{c}
0 \\
0 \\
-5
\end{array}\right]\)

Question 13.
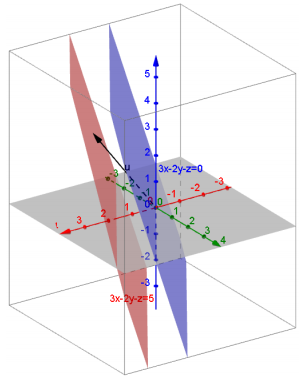
Given the vector v find the image of the given plane under the translation map T_v. Sketch the original vector and its image.

a. v = (2, -1, 3), 3x – 2y – z = 0
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x+2 \\
y-1 \\
z+3
\end{array}\right]\), 3x – 2y – z = 5

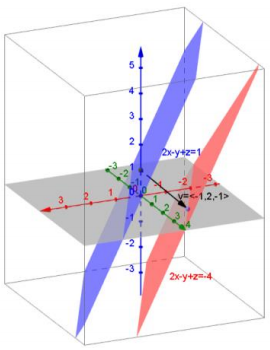
b. v = (-1, 2, -1), 2x – y + z = 1
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x-1 \\
y+2 \\
z-1
\end{array}\right]\), 2x – y + z = -4

Question 14.
Given the vector v find the knage of the given sphere under the translation map T_v. Sketch the original sphere and its image.

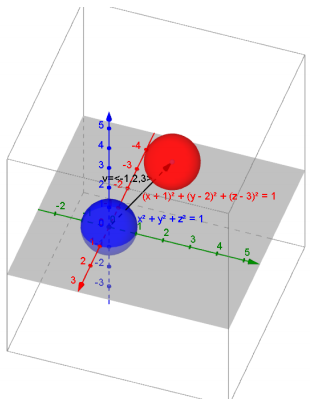
a. v = (-1, 2, 3), x² + y² + z² = 1
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x-1 \\
y+2 \\
z+3
\end{array}\right]\), (x + 1)² + (y – 2)² + (z – 3)² = 1

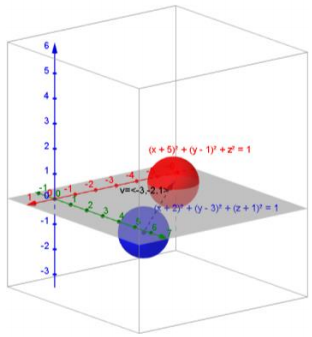
b. v = (-3, -2, 1), (x + 2)² + (y – 3)² + (z + 1)² = 1
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x-3 \\
y-2 \\
z+1
\end{array}\right]\), (x + 5)² + (y – 1)² + (z)² = 1

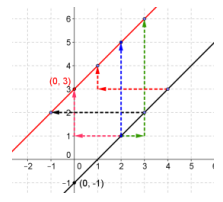
Question 15.
Find a vector v and translation map T_v that will translate the line x – y = 1 to the line x – y = -3. Sketch the original vector and its image.
Answer:
Answers vary. For example, v = \(\left[\begin{array}{l}
0 \\
4
\end{array}\right]\) and T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+0 \\
y+4
\end{array}\right]\).

Question 16.
Find a vector y and translation map T that will translate the parabola y = x² + 4x + 1 to the parabola y = x²
Answer:
Because y = x² + 4x + 1 can be written as y + 3 = (x + 2)², v = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\) and T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x+2 \\
y+3
\end{array}\right]\).

Question 17.
Find a vector v and translation map T_v that will translate the circle with equation x² + y² – 4x + 2y – 4 = 0 to the circle with equation (x + 3)² + (y – 4)² = g
Answer:
Because x² – 4x + y² + 2y = 4 can be written as (x – 2)² + (y + 1)² = 9, v = \(\left[\begin{array}{c}
-5 \\
5
\end{array}\right]\) and T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x-5 \\
y+5
\end{array}\right]\)

Question 18.
Find a vector v and translation map T_v, that will translate the graph of y = \(\sqrt{x-3}\) + 2 to the graph of y = \(\sqrt{x+2}\) – 3.
Answer:
v = \(\left[\begin{array}{l}
-5 \\
-5
\end{array}\right]\) and T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left[\begin{array}{l}
x-5 \\
y-5
\end{array}\right]\)

Question 19.
Find a vector y and translation map T_v that will translate the sphere (x + 2)² + (y – 3)² + (z + 1)² = 1 to the sphere (x – 3)2 + (y + 1)2 + (z + 2)2 = 1
Answer:
v = \(\left[\begin{array}{c}
5 \\
-4 \\
-1
\end{array}\right]\) and T_v\(\left(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\right)=\left[\begin{array}{l}
x+5 \\
y-4 \\
z-1
\end{array}\right]\)

20.
Given vectors u = (2, -1, 3), v = (2, 0, -2), and w = (-3, 6, 0), find the following.

a. 3u + v + w
Answer:
(5, 3, 7)

b. w – 2v – u
Answer:
(-9, 7, 1)

c. 3(2u – \(\frac{1}{2}\)v) – \(\frac{1}{3}\)w
Answer:
(10, -8, 21)

d. -2u – 3(5v – 3w)
Answer:
(-61, 56, 24)

e. ||u||, ||v||, and ||w||
Answer:
||u|| = √14, ||v|| = 2√2, ||w|| = √45

f. Show that 2||v|| = ||2v||
Answer:
2||v|| = 2(2√2) = 4√2, ||2v|| = ||(4, 0, -4)|| = √32 = 4√2

g. Show that |u + v|| ≠ ||u|| + ||v||
Answer:
||u + v|| = ||(4, -1, 1)|| = √18, ||u|| + ||v|| = √14 + 2√2

h. Show that ||v – w|| ≠ ||v|| – ||w||.
Answer:
||v – w|| = ||(5, -6, -2)|| = √65, ||v|| – ||w|| = 2√2 – √45

i. \(\frac{\mathbf{1}}{\|\mathbf{u}\|}\)u and \(\left\|\frac{\mathbf{1}}{\|\mathbf{u}\|} \mathbf{u}\right\|\)
Answer:

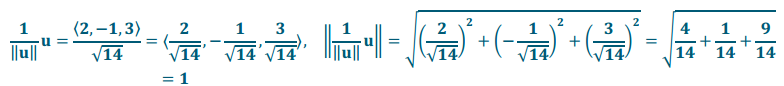
Eureka Math Precalculus Module 2 Lesson 18 Exit Ticket Answer Key

Question 1.
Given the vector v = (-2, 1), find the image of the line 3x – 2y = 2 under the translation map T_v. Graph the original line and its image, and explain the geometric effect of the map T_v.

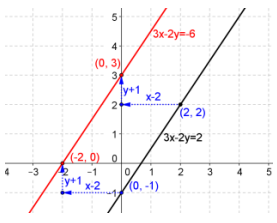
Answer:
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left(\begin{array}{l}
x-2 \\
y+1
\end{array}\right)\); image of the original line: 3(x + 2) – 2(y – 1) = 2.
3x + 6 – 2y + 2 = 2, 3x – 2y = -6
Every point on the line is shifted 2 units to the left and 1 unit upward.

Question 2.
Given the vector v = (-1, 2), find the image of the circle (x – 2)² + (y ÷ 1)² = 4 under the translation map T_v. Graph the original circle and its image, and explain the geometric effect of the map T_v.
Answer:

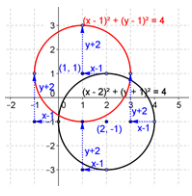
T_v\(\left(\left[\begin{array}{l}
x \\
y
\end{array}\right]\right)=\left(\begin{array}{l}
x-1 \\
y+2
\end{array}\right)\); image of original circle: (x – 1)² + (y – 1)² = 4.
Every point on the circle is shifted one unit to the left and two units upward. The new center is(1, 1) and the radius r = 2 stays the same.