Engage NY Eureka Math Precalculus Module 2 Lesson 16 Answer Key
Eureka Math Precalculus Module 2 Lesson 16 Example Answer Key
Example:
A scientist measured the greatest linear dimension of several irregular metal objects. He then used water displacement to calculate the volume of each of the objects. The data he collected are (1, 3), (2, 5), (4, 9), and (6, 20), where the first coordinate represents the linear measurement of the object in centimeters, and the second coordinate represents the volume in cubic centimeters. Knowing that volume measures generally vary directly with the cubed value of linear measurements, he wants to try to fit this data to a curve in the form of v(x) = ax3 + bx2 + cx + d.
a. Represent the data using a system of equations.
Answer:
3 = a + b + c + d
5 = 8a + 4b + 2c + d
9 = 64a + 16b + 4c + d
20 = 216a + 36b + 6c + d
b. Represent the system using a matrix equation in the form Ax = b.
Answer:
\(\left[\begin{array}{cccc}
1 & 1 & 1 & 1 \\
8 & 4 & 2 & 1 \\
64 & 16 & 4 & 1 \\
216 & 36 & 6 & 1
\end{array}\right]\left[\begin{array}{l}
a \\
b \\
c \\
d
\end{array}\right]=\left[\begin{array}{c}
3 \\
5 \\
9 \\
20
\end{array}\right]\)
c. Use technology to solve the system.
Answer:
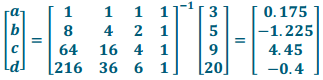
d. Based on your solution to the system, what cubic equation models the data?
Answer:
v(x) = 0.175x3 – 1.225x2 + 4.45x – 0.4
e. What are some of the limitations of the model?
Answer:
It is based off of only four points, so the equation goes exactly through all the points.
Eureka Math Precalculus Module 2 Lesson 16 Exercise Answer Key
Exercises:
Exercise 1.
An attendance officer in a small school district noticed a trend among the four elementary schools in the district. This district used an open enrollment policy, which means any student within the district could enroll at any school in the district.
Each year, 10% of the students from Adams Elementary enrolled at Davis Elementary, and 10% of the students from Davis enrolled at Adams. In addition, 10% of the students from Brown Elementary enrolled at Carson Elementary, and 20% of the students from Brown enrolled at Davis.
At Carson Elementary, about 10% of students enrolled at Brown, and 10% enrolled at Davis, while at Davis, 10% enrolled at Brown, and 20% enrolled at Carson. The officer noted that this year, the enrollment was 490, 250, 300, and 370 at Adams, Brown, Carson, and Davis, respectively.
a. Represent the relationship that reflects the annual movement of students among the elementary schools using a matrix.
Answer:
A = \(\left[\begin{array}{cccc}
0.9 & 0 & 0 & 0.1 \\
0 & 0.7 & 0.1 & 0.2 \\
0 & 0.1 & 0.8 & 0.1 \\
0.1 & 0.1 & 0.2 & 0.6
\end{array}\right]\)
b. Write an expression that could be used to calculate the attendance one year prior to the year cited by the attendance officer. Find the enrollment for that year.
Answer:
Expression = A-1b, where
b = \(\left[\begin{array}{l}
490 \\
250 \\
300 \\
370
\end{array}\right]\)
A-1b = \(\left[\begin{array}{l}
500 \\
200 \\
300 \\
400
\end{array}\right]\)
Enrollment one year prior to cited data: 500 at Adams, 250 at Brown, 300 at Carson, and 400 at Davis.
c. Assuming that the trend in attendance continues, write an expression that could be used to calculate the enrollment two years after the year cited by the attendance officer. Find the attendance for that year.
Answer:
Expression = A2b
A2b = \(\left[\begin{array}{l}
465.8 \\
296.7 \\
305.1 \\
349.7
\end{array}\right]\)
d. Interpret the results to part (c) in context.
Answer:
The approximate enrollment at the schools would be 466, 297, 305, and 350 for Adams, Brown, Carson, and Davis, respectively.
Exercise 2.
Mrs. Kenrick is teaching her class about different types of polynomials. They have just studied quartics, and she has offered 5 bonus points to anyone in the class who can determine the quartic that she has displayed on the board. The quartic has 5 points identified: (-6, 25), (-3, 1), (-2, \(\frac{7}{3}\)), (0, -5), and (3, 169). Logan really needs those bonus points and remembers that the general form for a quartic is y = ax4 + bx3 + cx2 + dx + e. Can you help Logan determine the equation of the quartic?
a. Write the system of equations that would represent this quartic.
Answer:
25 = 1296a – 216b + 36c – 6d + e
1 = 81a – 27b + 9c – 3d + e
\(\frac{7}{3}\) = 16a – 8b + 4c – 2d + e
-5 = e
169 = 81a + 27b + 9c + 3d + e
b. Write a matrix that would represent the coefficients of this quartic.
Answer:
A = \(\left[\begin{array}{ccccc}
1296 & -216 & 36 & -6 & 1 \\
81 & -27 & 9 & -3 & 1 \\
16 & -8 & 4 & -2 & 1 \\
0 & 0 & 0 & 0 & 1 \\
81 & 27 & 9 & 3 & 1
\end{array}\right]\)
c. Write an expression that could be used to calculate coefficients of the equation.
Answer:
Expression = A-1b, where
b = \(\left[\begin{array}{ccccc}
1296 & -216 & 36 & -6 & 1 \\
81 & -27 & 9 & -3 & 1 \\
16 & -8 & 4 & -2 & 1 \\
0 & 0 & 0 & 0 & 1 \\
81 & 27 & 9 & 3 & 1
\end{array}\right]\)
A-1b = \(\left[\begin{array}{c}
\frac{1}{3} \\
3 \\
7 \\
1 \\
-5
\end{array}\right]\)
d. Explain the answer in the context of this problem.
Answer:
a = \(\frac{1}{3}\), b = 3, c = 7 d = 1, c = -5
These are the coefficients of the quartic. The equation of the quartic is
y = \(\frac{1}{3}\)x4 + 3x3 + 7x2 + x – 5.
Exercise 3.
The Fibonacci numbers are the numbers 1, 1, 2, 3, 5, 8, 13, 21, 34, … Each number beyond the second is the sum
of the previous two. Let u1 = \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\), u2 = \(\left[\begin{array}{l}
1 \\
2
\end{array}\right]\), u3 = \(\left[\begin{array}{l}
2 \\
3
\end{array}\right]\), u4 = \(\left[\begin{array}{l}
3 \\
5
\end{array}\right]\), u5 = \(\left[\begin{array}{l}
5 \\
8
\end{array}\right]\), and so on.
a. Show that un + 1 = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 1
\end{array}\right]\) un.
Answer:
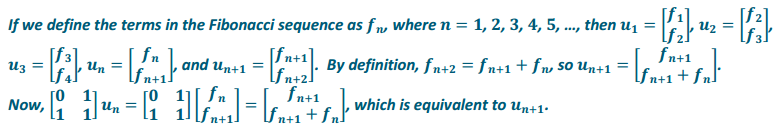
b. How could you use matrices to find u30? Use technology to find u30.
Answer:
u30 = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 1
\end{array}\right]^{29}\left[\begin{array}{l}
1 \\
1
\end{array}\right]=\left[\begin{array}{c}
832040 \\
1346269
\end{array}\right]\)
c. If un = \(\left[\begin{array}{l}
165580141 \\
267914296
\end{array}\right]\), find un – 1. Show your work.
Answer:
un – 1 = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 1
\end{array}\right]^{-1}\) un = \(\left[\begin{array}{c}
102334155 \\
165580141
\end{array}\right]\)
Eureka Math Precalculus Module 2 Lesson 16 Problem Set Answer Key
Question 1.
The system of equations is given:
1.2x + 3y – 5z + 4.2w + v = 0
6x = 5y + 2w
3y + 4. 5z – 6w +2v = 10
9x – y + z + 2v = -3
-4x + 2y – w + 3v = 1
a. Represent this system using a matrix equation.
Answer:
\(\left[\begin{array}{ccccc}
1.2 & 3 & -5 & 4.2 & 1 \\
6 & -5 & 0 & -2 & 0 \\
0 & 3 & 4.5 & -6 & 2 \\
9 & -1 & 1 & 0 & 2 \\
-4 & 2 & 0 & -1 & 3
\end{array}\right]=\left[\begin{array}{c}
x \\
y \\
z \\
w \\
v
\end{array}\right]=\left[\begin{array}{c}
0 \\
0 \\
10 \\
-3 \\
1
\end{array}\right]\)
b. Use technology to solve the system. Show your solution process, and round your entries to the tenths place.
Answer:

Question 2.
A caterer is preparing a fruit salad for a party. She decides to use strawberries, blackberries, grapes, bananas, and kiwi. The total weight of the fruit is 10 pounds. Based on guidelines from a recipe, the weight of the grapes is equal to the sum of the weight of the strawberries and blackberries; the total weight of the blackberries and kiwi is 2 pounds; half the total weight of fruit consists of kiwi, strawberries, and bananas; and the weight of the grapes is twice the weight of the blackberries.
a. Write a system of equations to represent the constraints placed on the caterer when she makes the fruit salad. Be sure to define your variables.
Answer:
S = pounds of strawberries
B = pounds of blackberries
G = pounds of grapes
K = pounds of kiwi
Ba = pounds of bananas
S + B + G + K + Ba = 10
G = S + B
B + K = 2
K + S + Ba = 5
G = 2B
b. Represent the system using a matrix equation.
Answer:
\(\left[\begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \\
-1 & -1 & 1 & 0 & 0 \\
0 & 1 & 0 & 1 & 0 \\
1 & 0 & 0 & 1 & 1 \\
0 & -2 & 1 & 0 & 0
\end{array}\right]\left[\begin{array}{c}
S \\
B \\
G \\
K \\
B a
\end{array}\right]=\left[\begin{array}{c}
10 \\
0 \\
2 \\
5 \\
0
\end{array}\right]\)
c. Solve the system using the matrix equation. Explain your solution in context.
Answer:
\(\left[\begin{array}{c}
S \\
B \\
G \\
K \\
B a
\end{array}\right]=\left[\begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \\
-1 & -1 & 1 & 0 & 0 \\
0 & 1 & 0 & 1 & 0 \\
1 & 0 & 0 & 1 & 1 \\
0 & -2 & 1 & 0 & 0
\end{array}\right]^{-1}\left[\begin{array}{c}
10 \\
0 \\
2 \\
5 \\
0
\end{array}\right]\) = \(\left[\begin{array}{c}
\frac{5}{3} \\
\frac{5}{3} \\
\frac{10}{3} \\
\frac{1}{3} \\
3
\end{array}\right]\)
The fruit salad consists of \(\frac{5}{3}\) pounds of strawberries, \(\frac{5}{3}\) pounds of blackberries, \(\frac{10}{3}\) pounds of grapes, \(\frac{1}{3}\)pound of kiwi, and 3 pounds of bananas.
d. How helpful would the solution to this problem likely be to the caterer as she prepares to buy the fruit?
Answer:
It is useful as a general guideline, but the caterer is unlikely to buy the fruit in exactly the amount indicated by the problem. For instance, it is unlikely that she could purchase exactly \(\frac{1}{3}\) pound of kiwi because it generally has to be purchased per fruit, not per ounce.
Question 3.
Consider the sequence 1, 1, 1, 3, 5, 9, 17, 31, 57, … where each number beyond the third is the sum of the previous three. Let wn be the points with the nth, (n + 1)th and (n + 2)th terms of the sequence.
a. Find a 3 × 3 matrix A so that Awn = wn + 1 for each n.
Answer:
A = \(\left[\begin{array}{lll}
0 & 1 & 0 \\
0 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]\)
b. What is the 30th term of the sequence?
Answer:
w30 = A29w1
= \(\left[\begin{array}{lll}
0 & 1 & 0 \\
0 & 0 & 1 \\
1 & 1 & 1
\end{array}\right]^{29}\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right]=\left[\begin{array}{l}
20603361 \\
37895489 \\
69700671
\end{array}\right]\)
c. What is A-1? Explain what A-1 represents in terms of the sequence. In other words, how can you find wn – 1 if you know wn?
Answer:
A-1 = \(\left[\begin{array}{ccc}
-1 & -1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array}\right]\)
The first entry of wn – 1 is the third entry from wn minus the sum of the first two entries of wn the second entry of wn – 1 is the first entry of wn and the third entry of wn – 1 is the second entry of wn.
d. Could you find the -5th term in the sequence? If so, how? What is its value?
Answer:
Yes.
W-5 = \(\left[\begin{array}{ccc}
-1 & -1 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array}\right]^{-6}\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right]=\left[\begin{array}{c}
1 \\
3 \\
-3
\end{array}\right]\)
Question 4.
Mr. Johnson completes a survey on the number of hours he spends weekly watching different types of television programs. He determines that he spends 30 hours a week watching programs of the following types: comedy, drama, movies, competition, and sports.
He spends half as much time watching competition shows as he does watching dramas. His time watching sports is double his time watching dramas. He spends an equal amount of tim watching comedies and movies. The total amount of time he spends watching comedies and movies is the same as the total amount of time he spends watching dramas and competition shows.
Write and solve a system of equations to determine how many hours Mr. Johnson watches each type of programming each week.
Answer:
Let f represent the hours watching comedy, d represent the hours watching drama, m represent the hours watching
movies, c represent the hours watching competition shows, and s represent the hours watching sports.
f + d + m + c + s = 30
0.5d = c
s = 2d
f = m
f + m = d + c
f = 4.5, d = 6, m = 4.5, c = 3, s = 12
\(\left|\begin{array}{ccccc}
1 & 1 & 1 & 1 & 1 \\
0 & 0.5 & 0 & -1 & 0 \\
0 & 0 & 0 & 0 & 0 \\
1 & 0 & -1 & 0 & 0 \\
1 & -1 & 1 & -1 & 0
\end{array}\right|\left|\begin{array}{c}
f \\
d \\
m \\
c \\
s
\end{array}\right|=\left|\begin{array}{c}
30 \\
0 \\
0 \\
0 \\
0
\end{array}\right|\)
Mr. Johnson spends 4.5 hours watching comedies, 6 hours watching dramas, 4.5 hours watching movies, 3 hours watching competition shows, and 12 hours watching sports each week.
Question 5.
A copper alloy is a mixture of metals having copper as their main component. Copper alloys do not corrode easily and conduct heat. They are used in all types of applications including cookware and pipes. A scientist is studying different types of copper alloys and has found one containing copper, zinc, tin, aluminum, nickel, and silicon. The alloy weighs 3.2 kilograms.
The percentage of aluminum is triple the percentage of zinc. The percentage of silicon is half that of zinc. The percentage of zinc is triple that of nickel. The percentage of copper is fifteen times the sum of the percentages of aluminum and zinc combined. The percentage of copper is nine times the combined percentages of all the other metals.
a. Write and solve a system of equations to determine the percentage of each metal in the alloy.
Answer:
Let c represent the percentage of copper, z represent the percentage of zinc, t represent the percentage of tin, a represent the percentage of aluminum, n represent the percentage of nickel, s represent the percentage of silicon.
c + z + t + a + n + s = 100
a = 3z
s = 0.5z
z = 3n
c = 15(a + z)
c = 9(z + t + a + n + s)
c = 90%, z = 1.5%, t = 2.75%, a = 4.5%, N = 0.5%, s = 0.75%
The alloy has 90% copper, 1.5% zinc, 2.75% tin, 4.5% aluminum, 0.5% nickel, and 0.75% silicon.
\(\left|\begin{array}{cccccc}
1 & 1 & 1 & 1 & 1 & 1 \\
0 & -3 & 0 & 1 & 0 & 0 \\
0 & -0.5 & 0 & 0 & 0 & 1 \\
0 & 1 & 0 & 0 & -3 & 0 \\
1 & -15 & 0 & -15 & 0 & 0 \\
1 & -9 & -9 & -9 & -9 & -9
\end{array}\right|\left|\begin{array}{c}
c \\
z \\
t \\
a \\
n \\
s
\end{array}\right|=\left|\begin{array}{c}
100 \\
0 \\
0 \\
0 \\
0 \\
0
\end{array}\right|\)
b. How many kilograms of each alloy are present in the sample?
Answer:
Copper: 0.90(3.2 kg) = 2.88 kg
Zinc: 0.015(3.2 kg) = 0.048 kg
Tin: 0.0275(3.2 kg) = 0.088 kg
Aluminum: 0.045(3.2 kg) = 0.144 kg
Nickel: 0.005(3.2 kg) = 0.016 kg
Silicon: 0.0075(3.2 kg) = 0.024 kg
Eureka Math Precalculus Module 2 Lesson 16 Exit Ticket Answer Key
Question 1.
Anabelle, Bryan, and Carl are playing a game using sticks of gum. For each round of the game, Anabelle gives half of her sticks of gum to Bryan and one-fourth to Carl. Bryan gives one-third of his sticks to Anabelle and keeps the rest. Carl gives 40 percent of his sticks of gum to Anabelle and 10 percent to Bryan. Sticks of gum can be cut into fractions when necessary.
a. After one round of the game, the players count their sticks of gum. Anabelle has 525 sticks, Bryan has 600, and Carl has 450. How many sticks of gum would each player have after 2 more rounds of the game? Use a matrix equation to represent the situation, and explain your answer in context.
Answer:
\(\left[\begin{array}{ccc}
\frac{1}{4} & \frac{1}{2} & \frac{1}{4} \\
\frac{1}{3} & \frac{2}{3} & 0 \\
\frac{2}{5} & \frac{1}{10} & \frac{1}{2}
\end{array}\right]^{2}\left[\begin{array}{l}
525 \\
600 \\
450
\end{array}\right]=x\)
x = \(\left[\begin{array}{cc}
547 \frac{3}{16} \\
564 \frac{7}{12} \\
522 \frac{1}{2}
\end{array}\right]\)
Anabelle would have 547\(\frac{3}{16}\) sticks of gum, Bryan would have 564\(\frac{7}{12}\) sticks, and Carl would have 522\(\frac{1}{2}\) sticks.
b. How many sticks of gum did each player have at the start of the game? Use a matrix equation to represent the situation, and explain your answer in context.
Answer:
\(\left[\begin{array}{lll}
\frac{1}{4} & \frac{1}{2} & \frac{1}{4} \\
\frac{1}{3} & \frac{2}{3} & 0 \\
\frac{2}{5} & \frac{1}{10} & \frac{1}{2}
\end{array}\right]^{-1}\left[\begin{array}{l}
525 \\
600 \\
450
\end{array}\right]\)
x = \(\left[\begin{array}{l}
600 \\
600 \\
300
\end{array}\right]\)
At the start of the game, Anabelle and Bryan each had 600 sticks of gum, and Carl had 300 sticks of gum.