Eureka Math Precalculus Module 2 Lesson 14 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 14 Answer Key

Eureka Math Precalculus Module 2 Lesson 14 Opening Exercise Answer Key

Opening Exercise:

Ahmad says the matrix \(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\) applied to the point \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\) will reflect the point to \(\left[\begin{array}{l}
1 \\
4
\end{array}\right]\) Randelle says that applying the matrix to the given point will produce a rotation of 1800 about the origin. Who is correct? Explain your answer and verify the result.
Answer:
Randelle is correct. Applying the matrix \(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\) to the given point produces a rotation of 180° about the origin of the \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\) point to the image point \(\left[\begin{array}{l}
-4 \\
-1
\end{array}\right]\). Applying the matrix \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) to the given point would produce a reflection to the image point \(\left[\begin{array}{l}
1 \\
4
\end{array}\right]\).

Eureka Math Precalculus Module 2 Lesson 14 Example Answer Key

Example:

a. Describe a transformation not already discussed that results in an image point of \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\) and represent the transformation using a 2 × 2.
Answer:
Answers will :ary. An example of an appropriate response is as follows: A rotation of the point \(\left[\begin{array}{c}
-1 \\
4
\end{array}\right]\) 90° to the point \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\) can be represented with the matrix \(\left[\begin{array}{cc}
0 & 1 \\
-1 & 0
\end{array}\right]\).

b. Determine whether any of the matrices listed represent linear transformations that can produce the image point \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\). Justify your answers by describing the transformations represented by the matrices.

i. \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
Answer:
This matrix represents a collapse to the origin, so it cannot produce the ima ge point \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\).

ii. \(\left[\begin{array}{ll}
1 & 1 \\
1 & 1
\end{array}\right]\)
Answer:
This matrix represents a transformation to the diagonal defined by y = x, so it cannot produce the image point \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\).

iii. \(\left[\begin{array}{ll}
0 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
This matrix represents a transformation to the y-axis, so it cannot produce the image point \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\).

c. Suppose a linear transformation L is represented by the matrix \(\left[\begin{array}{cc}
2 & -1 \\
3 & 1
\end{array}\right]\). Find a point L\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)so that L\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
4 \\
1
\end{array}\right]\).
Answer:
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
1 \\
-2
\end{array}\right]\)

Eureka Math Precalculus Module 2 Lesson 14 Exercise Answer Key

Exercises:

Exercise 1.
Given the system of equations
2x + 5y = 4
3x – 8y = -25

a. Show how this system can be written as a statement about a linear transformation of the form Lx = b, with x = \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) and b = \(\left[\begin{array}{c}
4 \\
-25
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
2 & 5 \\
3 & -8
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
4 \\
-25
\end{array}\right]\)

b. Determine whether L has an inverse. If it does, compute L^-1b, and verify that the coordinates represent the solution to the system of equations.
Answer:
L^-1b = \(\frac{1}{2(-8)-(5)(3)}\)\(\left[\begin{array}{cc}
-8 & -5 \\
-3 & 2
\end{array}\right]\left[\begin{array}{c}
4 \\
-25
\end{array}\right]\)

L^-1b = \(\frac{1}{-31}\)\(\left[\begin{array}{cc}
-8 & -5 \\
-3 & 2
\end{array}\right]\left[\begin{array}{c}
4 \\
-25
\end{array}\right]\)
= \(\frac{1}{-31}\)\(\left[\begin{array}{c}
93 \\
-62
\end{array}\right]\) = \(\left[\begin{array}{c}
-3 \\
2
\end{array}\right]\)

Verification using back substitution:
2(-3) + 5(2) = 4
3(-3) – 8(2) = -25

Exercise 2.
The path of a piece of paper carried by the wind into a tree can be modeled with a linear transformation, where L = \(\left[\begin{array}{cc}
3 & -4 \\
5 & 3
\end{array}\right]\) and b = \(\left[\begin{array}{c}
6 \\
10
\end{array}\right]\).

a. Write an equation that represents the linear transformation of the piece of paper.
Answer:
\(\left[\begin{array}{cc}
3 & -4 \\
5 & 3
\end{array}\right]\) \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
6 \\
10
\end{array}\right]\).

b. Solve the equation from part (a).
Answer:
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\frac{1}{29}\)\(\left[\begin{array}{cc}
3 & 4 \\
-5 & 3
\end{array}\right]\left[\begin{array}{c}
6 \\
10
\end{array}\right]\) = \(\frac{1}{29}\)\(\left[\begin{array}{c}
58 \\
0
\end{array}\right]\) = \(\left[\begin{array}{l}
2 \\
0
\end{array}\right]\)

c. Use your solution to provide a reasonable interpretation of the path of the piece of paper under the transformation by the wind.
Answer:
Answers will vary. An example of an appropriate response would be that the piece of paper started on the ground 2 feet to the right of the location defined as the origin, and it was moved by the wind to a spot 6 feet to the right of the origin and 10 feet above the ground (in the tree).

Exercise 3.
For each system of equations, write the system as a linear transformation represented by a matrix and apply inverse matrix operations to find the solution, or explain why this procedure cannot be performed.

a. 6x + 2y = 1
y = 3x + 1
Answer:

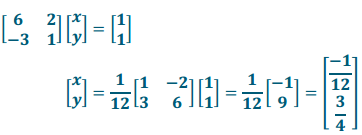
b. 4x – 6y = 10
2x – 3y = 1
Answer:
This system cannot be represented as a linear transformation because the transformation matrix L has a determinant of 0. The system represents parallel lines, so there is no solution.

Exercise 4.
In a two-dimensional plane, A represents a rotation of 30° counterclockwise about the origin, B represents a reflection over the line y = x, and C represents a rotation of 60° counterclockwise about the origin.

a. Write matrices A, B, and C.
Answer:
A = \(\left[\begin{array}{ll}
\frac{\sqrt{3}}{2} & -\frac{1}{2} \\
\frac{1}{2} & \frac{\sqrt{3}}{2}
\end{array}\right]\) B = \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) C = \(\left[\begin{array}{cc}
\frac{1}{2} & -\frac{\sqrt{3}}{2} \\
\frac{\sqrt{3}}{2} & \frac{1}{2}
\end{array}\right]\)

b. Transformations A, B, and C are applied to Point \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) successively and produce the image point \(\left[\begin{array}{c}
1+2 \sqrt{3} \\
2-\sqrt{3}
\end{array}\right]\). Use inverse matrix operations to find \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
Answer:
We must apply the inverse transformations in the reverse order. The inverse of matrix C
C^-1 = 1\(\left[\begin{array}{cc}
\frac{1}{2} & \frac{\sqrt{3}}{2} \\
-\frac{\sqrt{3}}{2} & \frac{1}{2}
\end{array}\right]\)
Applied to the image

Eureka Math Precalculus Module 2 Lesson 14 Problem Set Answer Key

Question 1.
In a two-dimensional plane, a transformation represented by L = \(\left[\begin{array}{cc}
1 & 5 \\
2 & -4
\end{array}\right]\) is applied to point x, resulting in an image point \(\left[\begin{array}{l}
0 \\
5
\end{array}\right]\). Find the location of the point before it was transformed.

a. Write an equation to represent the linear transformation of point x.
Answer:
\(\left[\begin{array}{cc}
1 & 5 \\
2 & -4
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
0 \\
5
\end{array}\right]\)

b. Solve the equation to find the coordinates of the pre-image point.
Answer:

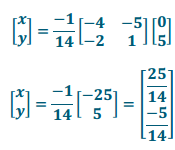
Question 2.
Find the location of the point \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) before it was transformed when given:

a. The transformation L = \(\left[\begin{array}{ll}
3 & 5 \\
1 & 2
\end{array}\right]\), and the resultant is \(\left[\begin{array}{l}
1 \\
2
\end{array}\right]\). Verify your answer.
Answer:

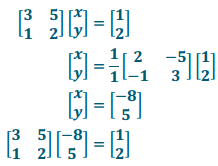
b. The transformation L = \(\left[\begin{array}{cc}
4 & 7 \\
-1 & -2
\end{array}\right]\) and the resultant is \(\left[\begin{array}{c}
2 \\
-1
\end{array}\right]\). Verify your answer.
Answer:

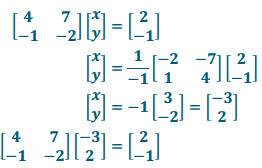
c. The transformation L = \(\left[\begin{array}{cc}
0 & -1 \\
2 & 1
\end{array}\right]\), and the reasultant is \(\left[\begin{array}{l}
1 \\
3
\end{array}\right]\). Verify your answer.
Answer:

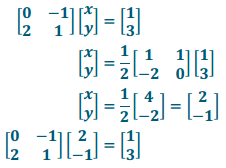
d. The transformation L = \(\left[\begin{array}{cc}
2 & 3 \\
0 & -1
\end{array}\right]\), and the resultant is \(\left[\begin{array}{l}
3 \\
0
\end{array}\right]\). Verify your answer.
Answer:

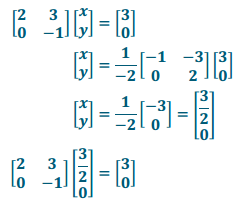
e. The transformation L = \(\left[\begin{array}{cc}
2 & -1 \\
1 & 2
\end{array}\right]\), and the reasultant is \(\left[\begin{array}{l}
3 \\
2
\end{array}\right]\). Verify your answer.
Answer:

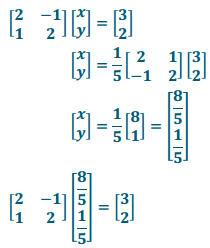
Question 3.
On a computer assembly line, a robot is placing a CPU onto a motherboard. The robot’s arm is carried out by the
transformation L = \(\left[\begin{array}{cc}
2 & 3 \\
1 & 2
\end{array}\right]\).

a. If the cu is attached to the motherboard at point \(\left[\begin{array}{l}
-2 \\
3
\end{array}\right]\), at what location does the robot pick up the CPU?
Answer:
\(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{c}
-2 \\
3
\end{array}\right]\)
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]=\frac{1}{1}\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\left[\begin{array}{c}
-2 \\
3
\end{array}\right]=\left[\begin{array}{c}
-13 \\
8
\end{array}\right]\)

b. If the CPU is attached to the motherboard at point \(\left[\begin{array}{l}
3 \\
2
\end{array}\right]\), at what location does the robot pick up the CPU?
Answer:
\(\left[\begin{array}{ll}
2 & 3 \\
1 & 2
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
3 \\
2
\end{array}\right]\)
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]=\frac{1}{1}\left[\begin{array}{cc}
2 & -3 \\
-1 & 2
\end{array}\right]\left[\begin{array}{l}
3 \\
2
\end{array}\right]=\left[\begin{array}{l}
0 \\
1
\end{array}\right]\)

c. Find the transformation L = \(\left[\begin{array}{cc}
-1 & c \\
b & 3
\end{array}\right]\) that places the CPU starting at \(\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\) onto the motherboard at the location \(\left[\begin{array}{c}
-8 \\
3
\end{array}\right]\)
Answer:
\(\left[\begin{array}{cc}
-1 & c \\
b & 3
\end{array}\right]\) \(\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\) = \(\left[\begin{array}{c}
-8 \\
3
\end{array}\right]\)
-2 – 3c = -8, c = 2
2b – 9 = 3, b = 6
\(\left[\begin{array}{cc}
-1 & 2 \\
6 & 3
\end{array}\right]\)

Question 4.
On a construction site, a crane is moving steel beams from a truck bed to workers. The crane is programmed to perform the transformation L = \(\left[\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right]\).

a. If the workers are at location \(\left[\begin{array}{l}
2 \\
5
\end{array}\right]\), where does the truck driver need to unload the steel beams so that the crane can pick them up and bring them to the workers?
Answer:
\(\left[\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
2 \\
5
\end{array}\right]\)
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]=\frac{1}{1}\left[\begin{array}{cc}
3 & -1 \\
-2 & 1
\end{array}\right]\left[\begin{array}{l}
2 \\
5
\end{array}\right]=\left[\begin{array}{l}
1 \\
1
\end{array}\right]\)

b. If the workers move to another location \(\left[\begin{array}{c}
-3 \\
1
\end{array}\right]\), where does the truck driver need to unload the steel beams so that the crane can pick them up and bring them to the workers?
Answer:
\(\left[\begin{array}{ll}
1 & 1 \\
2 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{c}
-3 \\
1
\end{array}\right]\)
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]=\frac{1}{1}\left[\begin{array}{cc}
3 & -1 \\
-2 & 1
\end{array}\right]\left[\begin{array}{c}
-3 \\
1
\end{array}\right]=\left[\begin{array}{c}
-10 \\
7
\end{array}\right]\)

Question 5.
A video game soccer player is positioned at \(\left[\begin{array}{l}
\mathbf{0} \\
2
\end{array}\right]\), where he kicks the ball. The ball goes into the goal, which is at point \(\left[\begin{array}{c}
10 \\
0
\end{array}\right]\). When the player moves to point \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\) and kicks the ball, he misses the goal. The ball lands at point \(\left[\begin{array}{l}
10 \\
-1
\end{array}\right]\).What is the program/transformation L = \(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\) that this video soccer player uses?
Answer:
\(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\left[\begin{array}{l}
0 \\
2
\end{array}\right]=\left[\begin{array}{c}
10 \\
0
\end{array}\right]\), 2c = 10, c = 5. 2d = 0, d = 0

\(\left[\begin{array}{ll}
a & 5 \\
b & 0
\end{array}\right]\left[\begin{array}{l}
1 \\
1
\end{array}\right]=\left[\begin{array}{l}
10 \\
-1
\end{array}\right]\), a + 5 = 10, a = 5, b = -1
\(\left[\begin{array}{cc}
5 & 5 \\
-1 & 0
\end{array}\right]\)

Question 6.
Tim bought 5 shirts and 3 pairs of pants, and it cost him $250. Scott bought 3 shirts and 2 pairs of pants, and It cost him $160. All the shirts have the same cost, and all the pants have the same cost.

a. Write a system of linear equations to find the cost of the shirts and pants.
Answer:
5S + 3P = 250
3S + 2P = 160

b. Show how this system can be written as a statement about a linear transformation of the form Lx = b with
x = \(\left[\begin{array}{l}
S \\
P
\end{array}\right]\) and b = \(\left[\begin{array}{l}
250 \\
160
\end{array}\right]\)
Answer:
\(\left[\begin{array}{ll}
5 & 3 \\
3 & 2
\end{array}\right]\left[\begin{array}{l}
S \\
P
\end{array}\right]=\left[\begin{array}{l}
250 \\
160
\end{array}\right]\)

c. Determine whether L has an inverse. If it does, compute L^-1b, and verify your answer to the system of equations.
Answer:
The determinant of \(\left[\begin{array}{ll}
5 & 3 \\
3 & 2
\end{array}\right]\) is 1. L^-1 = \(\frac{1}{1}\left[\begin{array}{cc}
2 & -3 \\
-3 & 5
\end{array}\right]\) = \(\left[\begin{array}{cc}
2 & -3 \\
-3 & 5
\end{array}\right]\)

\(\left[\begin{array}{l}
S \\
P
\end{array}\right]=\left[\begin{array}{cc}
2 & -3 \\
-3 & 5
\end{array}\right]\left[\begin{array}{l}
250 \\
160
\end{array}\right]=\left[\begin{array}{c}
20 \\
50
\end{array}\right]\)
Verification using back substitution: 5(20) + 3(50) = 250, 3(20) + 2(50) = 160.

Question 7.
In a two-dimensional plane, A represents a reflection over the x-axis, B represents a reflection over the y-axis, and C represents a reflection over the line y = x.

a. Write matrices A, B, and C.
Answer:
A = \(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\)
B = \(\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\)
C = \(\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]\)

b. Write an equation for each linear transformation, assuming that each one produces an image point of \(\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]\).
Answer:
For transformation A,
\(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]\)

For transformation B,
\(\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]\)

For transformation C,
\(\left[\begin{array}{cc}
0 & 1 \\
1 & 0
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]\)

c. Use inverse matrix operations to find the pre-image point for each equation. Explain how your solutions make sense based on your understanding of the effect of each geometric transformation on the coordinates of the pre-image points.
Answer:
For transformation A, \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = -1 \(\left[\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right]\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]=\left[\begin{array}{c}
-2 \\
3
\end{array}\right]\) When a point is reflected over the x-axis, the x-coordinate remains unchanged, and the y-coordinare changes signs.

For transformation B, \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = -1 \(\left[\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right]\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]=\left[\begin{array}{c}
2 \\
-3
\end{array}\right]\). When a point is reflected over the y-axis, the y-coordinate remains unchanged, and the x-coordinate changes signs.

For transformation C, \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{cc}
0 & -1 \\
-1 & 0
\end{array}\right]\left[\begin{array}{l}
-2 \\
-3
\end{array}\right]=\left[\begin{array}{l}
-3 \\
-2
\end{array}\right]\) When a point is reflected over the line y = x, the coordinates of the pre-image point are interchanged (x and y are switched).

Question 8.
A system of equations is shown:
2x + 5y + z = 3
4x + y – z = 5
3x + 2y + 4z = 1

a. Represent this system as a linear transformation in three-dimensional space represented by a matrix equation in the form of Lx = b.
Answer:
\(\left[\begin{array}{ccc}
2 & 5 & 1 \\
4 & 1 & -1 \\
3 & 2 & 4
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3 \\
5 \\
1
\end{array}\right]\)

b. What assumption needs to be made to solve the equation in part (a) for x.
Answer:
To use inverse operations, we need to assume that L has an inverse.

c. Use algebraic methods to solve the system.
Answer:
Adding equations 1 and 2 gives 6x + 6y = 8.
Adding 4 times equation 2 and equation 3 gives 19x + 6y = 21.
Subtracting (6x + 6y = 8) from (19x + 6y = 21) gives 13x = 13, so x = 1.
Back substituting into 6x + 6y = 8 gives 6y = 2, or y = \(\frac{1}{3}\)
Back substituting for y and x into the first equation gives 2(1) + 5(\(\frac{1}{3}\)) + z = 3, so z = –\(\frac{2}{3}\)
x = \(\left[\begin{array}{c}
1 \\
\frac{1}{3} \\
\frac{-2}{3}
\end{array}\right]\)

Question 9.
Assume L^-1 = \(\frac{1}{78}\left[\begin{array}{ccc}
-6 & 18 & 6 \\
19 & -5 & -6 \\
-5 & -11 & 18
\end{array}\right]\)
Use inverse matrix operations to solve the equation from Problem 8, part (a) for x. Verify that your solution is the same as the one you found in Problem 8, part (c).
Answer:
\(\left.\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) = \(\frac{1}{78}\left[\begin{array}{ccc}
-6 & 18 & 6 \\
19 & -5 & -6 \\
-5 & -11 & 18
\end{array}\right]\)\(\left[\begin{array}{l}
3 \\
5 \\
1
\end{array}\right]\) = \(\left[\begin{array}{c}
1 \\
\frac{1}{3} \\
\frac{-2}{3}
\end{array}\right]\),
which is the same solution found in part (c).

Eureka Math Precalculus Module 2 Lesson 14 Exit Ticket Answer Key

Question 1.
In two-dimensional space, point x is rotated 180° to the point \(\left[\begin{array}{l}
3 \\
4
\end{array}\right]\).

a. Represent the transformation of point x using an equation in the format Lx = b.
Answer:
\(\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
3 \\
4
\end{array}\right]\)

b. Use inverse matrix operations to find the coordinates of x.
Answer:
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]=\frac{1}{1}\left[\begin{array}{cc}
-1 & 0 \\
0 & -1
\end{array}\right]\left[\begin{array}{l}
3 \\
4
\end{array}\right]=\left[\begin{array}{l}
-3 \\
-4
\end{array}\right]\)

c. Verify that this solution makes sense geometrically.
Answer:
When a point is rotated 180° about the origin in the coordinate plane, the x- and y-coordinates of the image point are the opposite of those of the pre-image point.