Eureka Math Precalculus Module 2 Lesson 10 Answer Key

Engage NY Eureka Math Precalculus Module 2 Lesson 10 Answer Key

Eureka Math Precalculus Module 2 Lesson 10 Exercise Answer Key

Opening Exercise
Consider the vector v=\(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\).
If v is rotated 45° counterclockwise and then reflected across the y-axis, what is the resulting vector?
Answer:
\(\left(\begin{array}{c}
\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2}
\end{array}\right)\)

If v is reflected across the y-axis and then rotated 45° counterclockwise about the origin, what is the resulting vector?
Answer:
\(\left(\begin{array}{r}
-\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2}
\end{array}\right)\)

Did these linear transformations commute? Explain.
Answer:
No R_0,45°∘R_y≠R_y∘R_0,45°

Exercises

Exercise 1.
Let A equal the matrix that corresponds to a 45° rotation counterclockwise and B equal the matrix that corresponds to a reflection across the y-axis. Verify that matrix multiplication does not commute by finding the products AB and BA.
Answer:

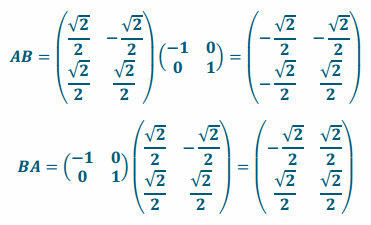
AB≠BA

Exercise 2.
Let A=\(\left(\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1
\end{array}\right)\) and B=\(\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{array}\right)\). Verify that matrix multiplication does not commute by finding the products AB and BA.
Answer:
AB=\(\left(\begin{array}{lll}
0 & 0 & 1 \\
1 & 0 & 0 \\
0 & 1 & 0
\end{array}\right)\)
BA=\(\left(\begin{array}{ccc}
0 & -1 & 0 \\
0 & 0 & -1 \\
1 & 0 & 0
\end{array}\right)\)
AB≠BA

Exercise 3.
Consider the vector v=\(\left(\begin{array}{l}
0 \\
0 \\
1
\end{array}\right)\).
a. If v is rotated 45° counterclockwise about the z-axis and then reflected across the xy-plane, what is the resulting vector?
Answer:
\(\left(\begin{array}{c}
\mathbf{0} \\
\mathbf{0} \\
-\mathbf{1}
\end{array}\right)\)

b. If v is reflected across the xy-plane and then rotated 45° counterclockwise about the z-axis, what is the resulting vector?
Answer:
\(\left(\begin{array}{c}
0 \\
0 \\
-1
\end{array}\right)\)

c. Verify algebraically that the product of the two corresponding matrices is the same regardless of the order in which they are multiplied.
Answer:
Let A=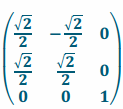 (the matrix representing 45° rotation about the z-axis).
Let B=\(\left(\begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & -1
\end{array}\right)\) (the matrix representing a reflection across the xy-plane).

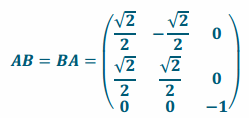
Exercise 4.
Write two matrices in the form \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right) .\)

a. Verify algebraically that the products of these two matrices are equal.
Let A=\(\left(\begin{array}{cc}
2 & -1 \\
1 & 2
\end{array}\right)\) and B=\(\left(\begin{array}{cc}
3 & -2 \\
2 & 3
\end{array}\right)\)
AB=\(\left(\begin{array}{cc}
4 & -7 \\
7 & 4
\end{array}\right)\) and BA=\(\left(\begin{array}{cc}
4 & -7 \\
7 & 4
\end{array}\right)\)
AB=BA

b. Write each of your matrices as a complex number. Find the product of the two complex numbers.
Answer:
(2+i)(3+2i)=4+7i

c. Why is it the case that any two matrices in the form \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\) have products that are equal regardless of the order in which they are multiplied?
Answer:
Matrices in this form represent the geometric effect of complex multiplication. Multiplying a complex number z by a complex number α and then by a complex number β gives the same answer as multiplying by β and then α; that is, β(αz)=α(βz); thus, the corresponding matrix multiplication yields the same product.

Eureka Math Precalculus Module 2 Lesson 10 Problem Set Answer Key

Question 1.
Let A be the matrix representing a dilation of 2, B the matrix representing a rotation of 30°, and x=\(\left(\begin{array}{c}
-2 \\
3
\end{array}\right)\).
a. Evaluate AB.
Answer:
\(\left(\begin{array}{cc}
\sqrt{3} & -1 \\
1 & \sqrt{3}
\end{array}\right)\)

b. Evaluate BA.
Answer:
\(\left(\begin{array}{cc}
\sqrt{3} & -1 \\
1 & \sqrt{3}
\end{array}\right)\)

c. Find ABx.
Answer:
\(\left(\begin{array}{l}
-2 \sqrt{3}-3 \\
-2+3 \sqrt{3}
\end{array}\right)\)

d. Find BAx.
Answer:
\(\left(\begin{array}{l}
-2 \sqrt{3}-3 \\
-2+3 \sqrt{3}
\end{array}\right)\)

Question 2.
Let A be the matrix representing a reflection across the line y=x, B the matrix representing a rotation of 90°, and x=\(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\).

a. Evaluate AB.
Answer:
\(\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\)

b. Evaluate BA.
Answer:
\(\left(\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right)\)

c. Find Ax.
Answer:
\(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\)

d. Find Bx.
Answer:
\(\left(\begin{array}{l}
0 \\
1
\end{array}\right)\)

e. Find ABx.
Answer:
\(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\)

f. Find BAx.
Answer:
\(\left(\begin{array}{l}
-1 \\
0
\end{array}\right)\)

g. Describe the linear transformation represented by AB.
Answer:
AB represents a reflection across the x-axis.

h. Describe the linear transformation represented by BA.
Answer:
BA represents a reflection across the y-axis.

Question 3.
Let matrices A,B represent scalars. Answer the following questions.
a. Would you expect AB=BA? Explain why or why not.
Answer:
Yes, scalars are real numbers, and real numbers commute.

b. Let A=\(\left(\begin{array}{cc}
a & 0 \\
0 & a
\end{array}\right)\) and B=\(\left(\begin{array}{ll}
b & 0 \\
0 & b
\end{array}\right)\). Show AB=BA through matrix multiplication, and explain why.
Answer:
AB=\(\left(\begin{array}{cc}
\boldsymbol{a} \boldsymbol{b} & \mathbf{0} \\
\mathbf{0} & \boldsymbol{a} \boldsymbol{b}
\end{array}\right)\)=\(\left(\begin{array}{cc}
b a & 0 \\
0 & b a
\end{array}\right)\)=BA
These matrices represent complex numbers and are both of the form \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\), so their products will be the same regardless of the order.

Question 4.
Let matrices A,B represent complex numbers. Answer the following questions.
a. Let A=\(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\) and B=\(\left(\begin{array}{cc}
c & -d \\
d & c
\end{array}\right)\). Show AB=BA through matrix multiplication.
Answer:

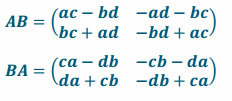
They are equivalent.

b. Would you expect AC=CA for any matrix C? Explain.
Answer:
No, matrix multiplication is not commutative.

c. Let C be any 2×2 matrix, \(\left(\begin{array}{ll}
x & y \\
z & w
\end{array}\right)\). Show AC≠CA through matrix multiplication.
Answer:

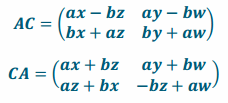
d. Summarize your results from Problems 3 and 4.
Answer:
Matrices representing scalars commute with any other matrix, and matrices representing complex number multiplication only commute when multiplying by other complex numbers (or if b=0).

Question 5.
Quaternions are a number system that extends to complex numbers discovered by William Hamilton in 1843. Multiplication of quaternions is not commutative and is defined as the quotient of two vectors. They are useful in three-dimensional rotation calculations for computer graphics. Quaternions are formed the following way:
i²²=j²=k²=ijk=-1
Multiplication by -1 and 1 works normally. We can represent all possible multiplications of quaternions through a table:

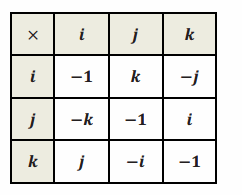
a. Is multiplication of quaternions commutative? Explain why or why not.
Answer:
No, it is not commutative. For example, ij=k, but ji=-k.

b. Is multiplication of quaternions associative? Explain why or why not.
Answer:
Yes, it is associative. i(jk)=i(i)=-1, and (ij)k=(k)k=-1 1 and -1 work normally.

Eureka Math Precalculus Module 2 Lesson 10 Exit Ticket Answer Key

Question 1.
Let A be the matrix representing a rotation about the origin by 60° and B be the matrix representing a reflection across the x-axis.
a. Give two reasons why AB≠BA.
Answer:
The linear transformations these matrices represent do not commute, and the matrices themselves do not commute.

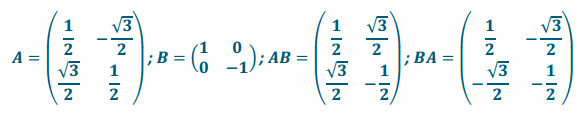
b. Let x=\(\left(\begin{array}{c}
1 \\
-1
\end{array}\right)\). Evaluate A(Bx) and B(Ax).
Answer:

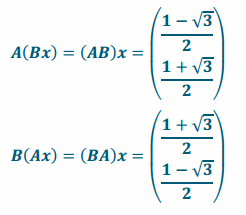
Question 2.
Write two matrices, A, B, that represent linear transformations where A(Bx) and B(Ax) where x=\(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\). Explain why the products are the same.
Answer:
Answers may vary. Examples include any two rotations about the origin, any two matrices representing complex numbers, and a dilation with any other matrix (since scalars commute with all matrices). For example:
A=\(\left(\begin{array}{ll}
2 & 0 \\
0 & 2
\end{array}\right)\), B=\(\left(\begin{array}{cc}
1 & -1 \\
1 & 1
\end{array}\right)\)
AB=BA=\(\left(\begin{array}{cc}
2 & -2 \\
2 & 2
\end{array}\right)\)
A(Bx)=B(Ax)=\(\left(\begin{array}{c}
2 \\
10
\end{array}\right)\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\)
Matrices in the form \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\) represent the geometric effect of complex multiplication. Multiplying a complex number z by a complex number α and then by a complex number β gives the same answer as multiplying by β and then α; that is, β(αz)=α(βz); thus, the corresponding matrix multiplication yields the same product.