Eureka Math Precalculus Module 1 Lesson 3 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 3 Answer Key

Eureka Math Precalculus Module 1 Lesson 3 Exercise Answer Key

Opening Exercise

Recall from the previous two lessons that a linear transformation is a function f that satisfies two conditions:
(1) f(x + y) = f(x) + f(y) and (2) f(kx) = kf(x). Here, k refers to any real number, and x and y represent arbitrary elements in the domain of f.

a. Let f(x) = x². Is f a linear transformation? Explain why or why not.
Answer:
Let x be 2 and y be 3. f(2 + 3) = f(5) = 5² = 25, but f(2) + f(3) = 22 + 32 = 4 + 9 = 13. Since these two values are different, we can conclude that f is not a linear transformation.

b. Let g(x) = \(\sqrt{x}\). Is g a linear transformation? Explain why or why not.
Answer:
Let x be 2 and y be 3. g(2 + 3) = g(5) = \(\sqrt{5}\), but g(2) + g(3) = \(\sqrt{2}\) + \(\sqrt{3}\), which is not equal to \(\sqrt{5}\). This means that g is not a linear transformation.

Eureka Math Precalculus Module 1 Lesson 3 Exit Ticket Answer Key

Suppose you have a linear transformation f: R → R, where f(3) = 9 and f(5) = 15.

Question 1.
Use the addition property to compute f(8) and f(13).
Answer:
f(8) = f(3 + 5) = f(3) + f(5) = 9 + 15 = 24
f(13) = f(8 + 5) = f(8) + f( 5) = 24 + 15 = 39

Question 2.
Find f(12) and f(10). Show your work.
Answer:
f(12) = f(4 ∙ 3) = 4 ∙ f(3) = 4 ∙ 9 = 36
f(10) = f(2 ∙ 5) = 2 ∙ f(5) = 2 ∙ 15 = 30

Question 3.
Find f(-3) and f(-5). Show your work.
Answer:
f(-3) = -f(3) = -9
f(-5) = -f(5) = -15

Question 4.
Find f(0). Show your work.
Answer:
f(0) = f(3 + -3) = f(3) + f(-3) = 9 + -9 = 0

Question 5.
Find a formula for f(x).
Answer:
We know that there is some number a such that f(x) = ax, and since f(3) = 9, the value of a = 3. In other words, f(x) = 3x. We can also check to see if f(5) = 15 is consistent with a = 3, which it is.

Question 6.
Draw the graph of the function y = f(x).
Answer:

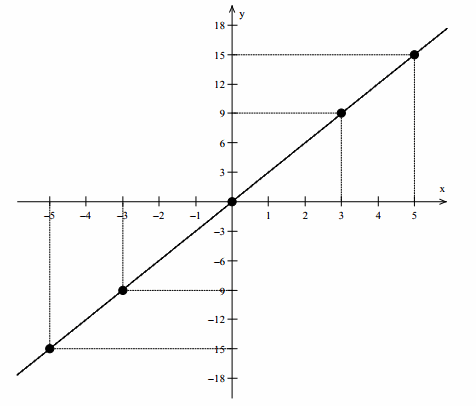
Eureka Math Precalculus Module 1 Lesson 3 Problem Set Answer Key

The first problem provides students with practice in the core skills for this lesson. The second problem is a series of exercises in which students explore concepts of linearity in the context of integer-valued functions as opposed to real¬valued functions. The third problem plays with the relation f(x + y) = f(x) + f(y), exchanging addition for multiplication in one or both expressions.

Question 1.
Suppose you have a linear transformation f: R → R, where f(2) = 1 and f(4) = 2.

a. Use the addition property to compute f(6), f(8), f(10), and f(12).
Answer:
f(6) = f(2 + 4) = f(2) + f(4) = 1 + 2 = 3
f(8) = f(2 + 6) = f(2)+ f(6) = 1 + 3 = 4
f(10) = f(4 + 6) = f(4) + f(6) = 2 + 3 = 5
f(12) = f(10 + 2) = f(10) + f(2) = 5 + 1 = 6

b. Find f(20), f(24), and f(30). Show your work.
Answer:
f(20) = f(10 ∙ 2) = 10 ∙ f(2) = 10 ∙ 1 = 10
f(24) = f(6 ∙ 4) = 6 ∙ f(4) = 6 ∙ 2 = 12
f(30) = f(15 ∙ 2) = 15 ∙ f(2) = 15 ∙ 1 = 15

c. Find f(-2), f(-4), and f(-8). Show your work.
Answer:
f(-2) = f(-1 ∙ 2) = -1 ∙ f(2) = -1 – 1 = -1
f(-4) = f(-1 ∙ 4) = -1 ∙ f(4) = -1 – 2 = -2
f(-8) = f(-2 ∙ 4) = -2 ∙ f(4) = -2 ∙ 2 = -4

d. Find a formula for f(x).
Answer:
We know there is some number a such that f(x) = ax, and since f(2) = 1, then the value of a = \(\frac{1}{2}\).
In other words, f(x) = \(\frac{x}{2}\). We can also check to see if f(4) = 2 is consistent with a = \(\frac{1}{2}\) which it is.

e. Draw the graph of the function f(x).
Answer:

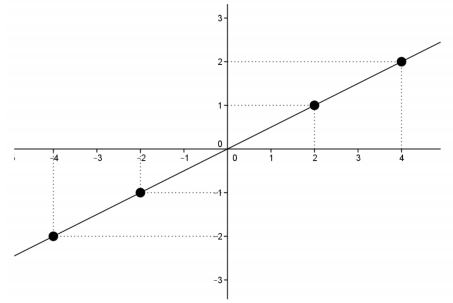
Question 2.
The symbol L represents the set of integers, and so g: Z → Z represents a function that takes integers as inputs and produces integers as outputs. Suppose that a function g: Z → Z satisfies g(a + b) = g(a) + g(b) for all integers a and b. Is there necessarily an integer k such that g(n) = kn for all integer inputs n?

a. Let k = g(1). Compute g(2) and g(3).
Answer:
g(2) = g(1 + 1) = g(1) + g(1) = k + k = 2k
g(3) = g(1 + 1 + 1) = g(1) + g(1) + g(1) = k + k + k = 3k

b. Let n be any positive integer. Compute g(n).
Answer:
g(n) = g(1 + …… + 1) = g(1) + ……. + g(1) = k + …… + k = nk

c. Now, consider g(0). Since g(0) = g(0 + 0), what can you conclude about g(0)?
Answer:
g(0) = g(0 + 0) = g(0) + g(0). By subtracting g(0) from both sides of the equation, we get g(0) = 0.

d. Lastly, use the fact that g(n +-n) = g(0) to learn something about g(-n), where n is any positive integer.
Answer:
g(0) = g(n + -n) = g(n) + g(-n). Since we know that g(0) = 0, we have g(n) + g(-n) = 0. This tells us that g(-n) = -g(n).

e. Use your work above to prove that g(n) = kn for every integer n. Be sure to consider the fact that n could be positive, negative, or 0.
Answer:
We showed that if n is a positive integer, then g(n) = kn, where k = g(1). Also, since k ∙ 0 = 0 and we showed that g(0) = 0, we have g(0) = k ∙ 0. Finally, if n is a negative integer, then -n is positive, which means g(-n) = k(-n) = -kn. But, since g(-n) = -g(n), we have g(n) = -g(-n) = -(-kn) = kn. Thus, in all cases, g(n) = kn.

Question 3.
In the following problems, be sure to consider all kinds of functions: polynomial, rational, trigonometric, exponential, logarithmic, etc.

a. Give an example of a function f: R → R that satisfies f(x ∙ y) = f(x) + f(y).
Answer:
Any logarithmic function works; for instance, f(x) = log(x).

b. Give an example of a function g: R → R that satisfies g(x + y) = g(x) ∙ g(y).
Answer:
Any exponential function works; for instance, g(x) = 2^x.

c. Give an example of a function h: R → R that satisfies h(x ∙ y) = h(x) ∙ h(y).
Answer:
Any power of x works; for instance, h(x) = x³.