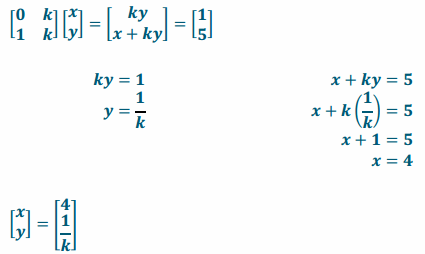Eureka Math Precalculus Module 1 Lesson 27 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 27 Answer Key

Eureka Math Precalculus Module 1 Lesson 27 Example Answer Key

Example 1.
Given the transformation \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\boldsymbol{k} & \mathbf{1}
\end{array}\right]\) with k>0:
a. Perform this transformation on the vertices of the unit square. Sketch the image, and label the vertices.
Answer:

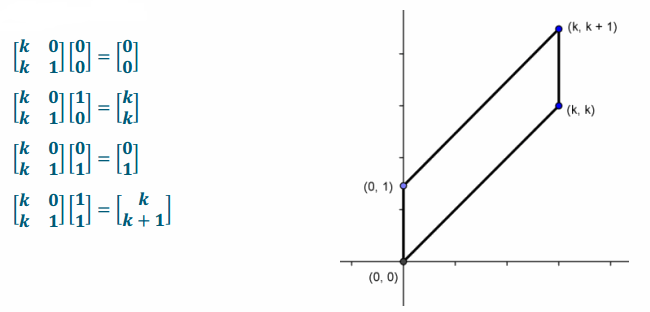
b. Calculate the area of the image using the dimensions of the image parallelogram.
Answer:
The parallelogram is 1 unit high, and the perpendicular distance between parallel bases is k units wide, so the area is 1∙k=k square units.

c. Confirm the area of the image using the determinant.
Answer:
The area of the unit square is 1, and the determinant of the transformation matrix is |(k)(1)-(0)(k)|=k. The area of the parallelogram is 1∙k=k square units. The area is confirmed.

d. Perform the transformation on \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
Answer:
\(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\boldsymbol{k} & \mathbf{1}
\end{array}\right]\left[\begin{array}{l}
\boldsymbol{x} \\
\boldsymbol{y}
\end{array}\right]\) = \(\left[\begin{array}{c}
k x \\
k x+y
\end{array}\right]\)

e. In order for two matrices to be equivalent, each of the corresponding elements must be equivalent. Given that, if the image of this transformation is \(\left[\begin{array}{l}
5 \\
4
\end{array}\right]\), find \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\).
Answer:
\(\left[\begin{array}{c}
\boldsymbol{k} \boldsymbol{x} \\
\boldsymbol{k} \boldsymbol{x}+\boldsymbol{y}
\end{array}\right]\)=\(\left[\begin{array}{l}
5 \\
4
\end{array}\right]\)
kx=5
x=\(\frac{5}{k}\)

kx+y=4
k(\(\frac{5}{k}\))+y=4
5+y=4
y=-1
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
\frac{5}{k} \\
-1
\end{array}\right]\)

f. Perform the transformation on \(\left[\begin{array}{l}
1 \\
1
\end{array}\right]\). Write the image matrix.
Answer:
\(\left[\begin{array}{ll}
k & 0 \\
k & 1
\end{array}\right]\left[\begin{array}{l}
1 \\
1
\end{array}\right]\) = \(\left[\begin{array}{c}
\boldsymbol{k} \\
\boldsymbol{k}+\mathbf{1}
\end{array}\right]\)

g. Perform the transformation on the image again, and then repeat until the transformation has been performed four times on the image of the preceding matrix.
Answer:

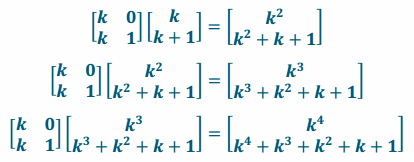
→ What are the vertices of the image?
→ (0,0), (k,k), (0,1), and (k,k+1)
→ What is the formula for the area of a parallelogram?
→ The area of a parallelogram is base×height.
→ What is the base and height of the parallelogram that is the image of this transformation? How do you know?
→ The base is the length of one of the parallel sides, which is 1 unit. The height is the perpendicular distance between parallel sides, and that is k units.
→ Using the formula, calculate the area of the parallelogram.
→ The area is k square units.
→ Now find the area using the determinant. Is the area confirmed?
→ Area=|(k)(1)-(0)k|=k square units. This is the same area.
→ Now perform the transformation on a point (x,y). What is the matrix that results?
→ \(\left[\begin{array}{c}
k x \\
k x+y
\end{array}\right]\)
→ If we want the image of this transformation on (x,y) to map to (5,4), how could we find (x,y)?
→ We could write a system of equations and solve for (x,y).
→ Write the system of equations.
→ kx=5
→ kx+y=4
→ Solve for x and y in terms of k. Which variable is easiest to solve for? Explain and solve for it.
→ It is easiest to solve for x because the first equation only has x, not y. x=\(\frac{5}{k}\)
→ Now solve for the other variable.
→ y=4-k(\(\frac{5}{k}\))=4-5=-1
→ So, \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) is equal to what?
→ \(\left[\begin{array}{c}
\frac{5}{k} \\
-1
\end{array}\right]\)

Eureka Math Precalculus Module 1 Lesson 27 Exercise Answer Key

Opening Exercise
Explain the geometric effect of each matrix.

a. \(\left[\begin{array}{cc}
a & -b \\
b & a
\end{array}\right]\)
Answer:
A rotation of arctan(latex]\left(\frac{b}{a}\right)[/latex] and a dilation with scale factor \(\sqrt{a^{2}+b^{2}}\)

b. \(\left[\begin{array}{cc}
\cos (\theta) & -\sin (\theta) \\
\sin (\theta) & \cos (\theta)
\end{array}\right]\)
Answer:
A pure rotation of θ

c. \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\mathbf{0} & \boldsymbol{k}
\end{array}\right]\)
Answer:
A pure dilation of scale factor k

d. \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
The multiplicative identify matrix has no geometric effect.

e. \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)
Answer:
The additive identify matrix maps all points to the origin.

f. \(\left[\begin{array}{ll}
a & c \\
b & d
\end{array}\right]\)
Answer:
Transforms the unit square to a parallelogram with vertices (0,0), (a,b), (c,d), and (a+c,b+d) with area of |ad-bc|.

Exercise 1.
Perform the transformation \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\mathbf{1} & \boldsymbol{k}
\end{array}\right]\) with k>1 on the vertices of the unit square.

a. What are the vertices of the image?
Answer:
(0,0), (k,1), (0,k), and (k,k+1)

b. Calculate the area of the image.
Answer:
k²

c. If the image of the transformation on \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) is \(\left[\begin{array}{l}
-2 \\
-1
\end{array}\right]\), find \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) in terms of k.
Answer:

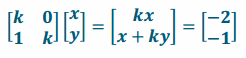
kx=-2
x=\(\frac{-2}{k}\) x+ky=-1
\(\frac{-2}{k}\)+ky=-1

x + ky=-1
\(\frac{-2}{k}\) + ky = -1
ky = -1 + \(\frac{2}{k}\)
y = \(\frac{-1}{k}\) + \(\frac{2}{k²}\)
\(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{c}
\frac{-2}{k} \\
\frac{-1}{k}+\frac{2}{k^{2}}
\end{array}\right]\)

Example 2.
Consider the matrix L=\(\left[\begin{array}{cc}
2 & 5 \\
-1 & 3
\end{array}\right]\). For each real number 0≤t≤1, consider the point (3+t,10+2t).

a. Find point A when t=0.
Answer:
A(3,10)

b. Find point B when t=1.
Answer:
B(4,12)

c. Show that for t=\(\frac{1}{2}\), (3+t,10+2t) is the midpoint of \(\overline{\boldsymbol{A B}}\).
Answer:
When t=\(\frac{1}{2}\), point M is (3+\(\frac{1}{2}\),10+2(\(\frac{1}{2}\))), or (3.5,11). The midpoint of \(\overline{\boldsymbol{A B}}\)is (\(\frac{3+4}{2}\),\(\frac{10+12}{2}\)), or (\(\frac{7}{2}\),11). The midpoint is at t=\(\frac{1}{2}\).

d. Show that for each value of t,(3+t,10+2t) is a point on the line through A and B.
Answer:
The equation of the line through A and B is y-10=\(\frac{12-10}{4-3}\)(x-3), or y-10=2(x-3), or y=2x+4. If we substitute (3+t,10+2t) into the equation, we get 10+2t=2(3+t)+4 or 10+2t=2t+10, which is a statement that is true for all real values of t. Therefore, the point (3+t,10+2t) lies on the line through A and B for all values of t.

e. Find LA and LB.
Answer:

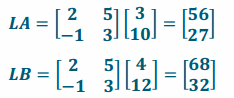
f. What is the equation of the line through LA and LB?
Answer:
The line through LA and LB is y-27=\(\frac{32-27}{68-56}\)(x-56) or y-27=\(\frac{5}{12}\)(x-56).

g. Show that L\(\left[\begin{array}{c}
3+t \\
10+2 t
\end{array}\right]\) lies on the line through LA and LB.
Answer:

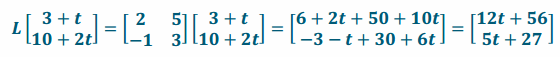
(5t+27)-27=\(\frac{5}{12}\)((12t+56)-56)
5t=5t, which is true for all real values of t, so L\(\left[\begin{array}{c}
3+t \\
10+2 t
\end{array}\right]\) and lies on the line through LA and LB.

Eureka Math Precalculus Module 1 Lesson 27 Problem Set Answer Key

Question 1.
Perform the following transformation on the vertices of the unit square. Sketch the image, label the vertices, and find the area of the image parallelogram.
a.\(\left[\begin{array}{ll}
1 & 0 \\
1 & 1
\end{array}\right]\)
Answer:

Area=|1×1-1×0|=1
The area is 1 units²

b. \(\left[\begin{array}{ll}
2 & 0 \\
2 & 1
\end{array}\right]\)
Answer:

Area=|2×1-2×0|=2
The area is 2 units².

c. \(\left[\begin{array}{ll}
3 & 0 \\
3 & 1
\end{array}\right]\)
Answer:

Area=|3×1-3×0|=3
The area is 3 units².

d. \(\left[\begin{array}{ll}
2 & 0 \\
2 & 2
\end{array}\right]\)
Answer:

Area=|2×2-2×0|=4
The area is 4 units².

e. \(\left[\begin{array}{ll}
3 & 0 \\
3 & 3
\end{array}\right]\)
Answer:

Area=|3×3-3×0|=9
The area is 9 units².

f. \(\left[\begin{array}{ll}
1 & 0 \\
1 & 2
\end{array}\right]\)
Answer:

Area=|1×2-1×0|=2
The area is 2 units².

g. \(\left[\begin{array}{ll}
1 & 0 \\
1 & 3
\end{array}\right]\)
Answer:

Area=|1×3-1×0|=3
The area is 3 units².

h. \(\left[\begin{array}{ll}
2 & 0 \\
2 & 3
\end{array}\right]\)
Answer:

Area=|2×3-2×0|=6
The area is 6 units².

i. \(\left[\begin{array}{ll}
3 & 0 \\
3 & 5
\end{array}\right]\)
Answer:

Area=|3×5-3×0|=15
The area is 15 units².

Question 2.
Given \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\boldsymbol{k} & \mathbf{1}
\end{array}\right]\left[\begin{array}{l}
\boldsymbol{x} \\
\boldsymbol{y}
\end{array}\right]\)=\(\left[\begin{array}{c}
\boldsymbol{k} \boldsymbol{x} \\
\boldsymbol{k} \boldsymbol{x}+\boldsymbol{y}
\end{array}\right]\). Find \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) if the image of the transformation is the following:

a. \(\left[\begin{array}{l}
4 \\
5
\end{array}\right]\)
Answer:

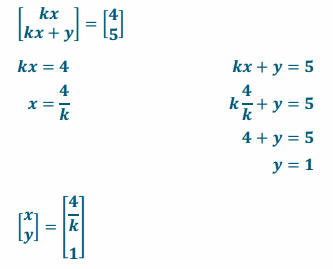
b. \(\left[\begin{array}{c}
-3 \\
2
\end{array}\right]\)
Answer:

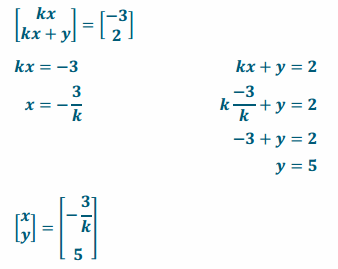
c. \(\left[\begin{array}{c}
5 \\
-6
\end{array}\right]\)
Answer:

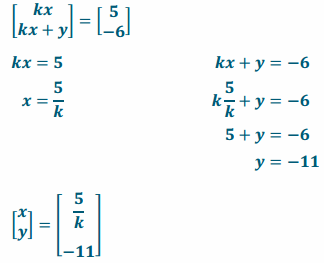
Question 3.
Given \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\boldsymbol{k} & \mathbf{1}
\end{array}\right]\left[\begin{array}{l}
\boldsymbol{x} \\
\boldsymbol{y}
\end{array}\right]\)=\(\left[\begin{array}{c}
k x \\
k x+y
\end{array}\right]\). Find the value of k so that:
a. \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) = \(\left[\begin{array}{l}
3 \\
-2
\end{array}\right]\) and the image is \(\left[\begin{array}{l}
24 \\
22
\end{array}\right]\).
Answer:

3k+0=24
k=8 OR 3k-2=22
k=8

b. \(\)=\(\) and the image is \(\).
Answer:

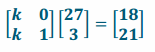
27k+0=18
k=\(\frac{18}{27}\)=\(\frac{2}{3}\)
OR
27k+3=21
k=\(\frac{18}{27}\)=\(\frac{2}{3}\)

Question 4.
Given \(\left[\begin{array}{ll}
k & 0 \\
1 & k
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]\)=\(\left[\begin{array}{c}
\boldsymbol{k} \boldsymbol{x} \\
\boldsymbol{x}+\boldsymbol{k} y
\end{array}\right]\). Find the value of k so that:

a. \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\)=\(\left[\begin{array}{l}
-4 \\
5
\end{array}\right]\) and the image is \(\left[\begin{array}{l}
-12 \\
11
\end{array}\right]\).
Answer:

-4k+0=-12
k=3 OR
-4+5k=11
k=3

b. \(\)=\(\) and the image is \(\).
Answer:

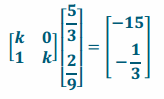
\(\frac{5}{3}\) k+0=-15
k=-9
OR \(\frac{5}{3}\)+\(\frac{2}{9}\) k=-\(\frac{1}{3}\)
k=-9

Question 5.
Perform the following transformation on the vertices of the unit square. Sketch the image, label the vertices, and find the area of the image parallelogram.
a. \(\left[\begin{array}{ll}
2 & 0 \\
1 & 2
\end{array}\right]\)
Answer:

Area=|k×k-1×0|=k²=4
The area is 4 units².

b. \(\left[\begin{array}{ll}
3 & 0 \\
1 & 3
\end{array}\right]\)
Answer:

Area=|k×k-1×0|=k²=9
The area is 9 units².

c. \(\)
Answer:

Area=|k×k-1×0|=k²=4
The area is 4 units².

d. \(\)
Answer:

Area=|k×k-1×0|=k²=4
The area is 4 units².

e. \(\)
Answer:

Area=|k×k-1×0|=k²=16
The area is 16 units².

f. \(\)
Answer:

Area=|k×k-1×0|=k²=9
The area is 9 units².

Question 6.
Consider the matrix L=\(\). For each real number 0≤t≤1, consider the point (3+2t,12+2t).
a. Find the point A when t=0.
Answer:
A(3,12)

b. Find the point B when t=1.
Answer:
B(5,14)

c. Show that for t=\(\frac{1}{2}\), (3+2t,12+2t) is the midpoint of \(\overline{\boldsymbol{A B}}\).
Answer:
When t=\(\frac{1}{2}\), the point M is (3+1,12+1), or (4,13).
And the midpoint of \(\overline{\boldsymbol{A B}}\)is ((3+5)/2,(12+14)/2), or (4,13). Thus, the midpoint is at t=\(\frac{1}{2}\).

d. Show that for each value of t, (3+2t,12+2t) is a point on the line through A and B.
Answer:
The equation of the line through \(\overline{\boldsymbol{A B}}\):
y-12=\(\frac{12-14}{3-5}\)(x-3)
y=x+9
If we substitute (3+2t,12+2t) into the equation, we get 12+2t=3+2t+9, or 12+2t=12+2t, which is a statement that is true for all real values of t. Therefore, the point (3+2t,12+2t) lies on the line through A and B for all values of t.

e. Find LA and LB.
Answer:

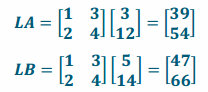
f. What is the equation of the line through LA and LB?
Answer:
y-54=\(\frac{66-54}{47-39}\)(x-39)
y-54=\(\frac{3}{2}\)(x-39)

g. Show that L\(\left[\begin{array}{c}
3+2 t \\
12+2 t
\end{array}\right]\) lies on the line through LA and LB.
Answer:

We substitute it into the equation in part (f):
54+12t-54=\(\frac{3}{2}\)(39+8t-39)
12t=\(\frac{3}{2}\) (8t)
12t=12t,
which is true for all real values of t, so \(\left[\begin{array}{c}
3+2 t \\
12+2 t
\end{array}\right]\) lies on the line through LA and LB.

Eureka Math Precalculus Module 1 Lesson 27 Exit Ticket Answer Key

Given the transformation \(\left[\begin{array}{ll}
\mathbf{0} & \boldsymbol{k} \\
\mathbf{1} & \boldsymbol{k}
\end{array}\right]\) with k>0:

a. Find the area of the image of the transformation performed on the unit matrix.
Answer:
|(0)(k)-(k)(1)|=|-k|=k

b. The image of the transformation on \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) is \(\left[\begin{array}{l}
1 \\
5
\end{array}\right]\); find \(\left[\begin{array}{l}
x \\
y
\end{array}\right]\) in terms of k. Show your work.
Answer: