Eureka Math Precalculus Module 1 Lesson 25 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 25 Answer Key

Eureka Math Precalculus Module 1 Lesson 25 Example Answer Key

Example 1.
Is Matrix Multiplication Commutative?
a. Take the point \(\left(\begin{array}{l}
2 \\
1
\end{array}\right)\) through the following transformations: a rotation of \(\frac{π}{2}\) and a reflection across the y-axis.
Answer:
\(\left(\begin{array}{l}
1 \\
2
\end{array}\right)\)

b. Will the resulting point be the same if the order of the transformations is reversed?
Answer:
No, if the reflection is applied first, followed by the rotation, the resulting point is \(\left(\begin{array}{l}
-1 \\
-2
\end{array}\right)\).

c. Are transformations commutative?
Answer:
Not necessarily; the order in which the transformations are applied can affect the results in some cases.

d. Let A=\(\left(\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right)\) and B=\(\left(\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right)\). Find AB and then BA.
Answer:

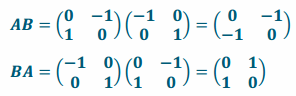
e. Is matrix multiplication commutative?
Answer:
No, AB≠BA

f. If we apply matrix AB to the point \(\left(\begin{array}{l}
2 \\
1
\end{array}\right)\), in what order are the transformations applied?
Answer:

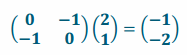
The reflection is applied first, followed by the dilation.

g. If we apply matrix BA to the point \(\left(\begin{array}{l}
2 \\
1
\end{array}\right)\), in what order are the transformations applied?
Answer:

The dilation is applied first, followed by the reflection.

h. Can we apply \(\left(\begin{array}{l}
2 \\
1
\end{array}\right)\) to matrix BA?
Answer:

No, \(\left(\begin{array}{l}
2 \\
1
\end{array}\right)\) has two rows and one column. It would have to have two columns to be able to multiply by the 2×2 matrix BA.

Eureka Math Precalculus Module 1 Lesson 25 Exercise Answer Key

Opening Exercise

Consider the point \(\left(\begin{array}{l}
4 \\
1
\end{array}\right)\) that undergoes a series of two transformations: a dilation of scale factor 4 followed by a reflection about the horizontal axis.

a. What matrix produces the dilation of scale factor 4? What is the coordinate of the point after the dilation?
Answer:
The dilation matrix is \(\left(\begin{array}{ll}
4 & 0 \\
0 & 4
\end{array}\right)\).

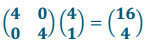
The coordinate is now \(\left(\begin{array}{c}
16 \\
4
\end{array}\right)\).

b. What matrix produces the reflection about the horizontal axis? What is the coordinate of the point after the reflection?
Answer:
The reflection matrix is \(\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\).

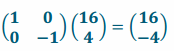
The coordinate is now \(\left(\begin{array}{c}
16 \\
-4
\end{array}\right)\).

c. Could we have produced both the dilation and the reflection using a single matrix? If so, what matrix would both dilate by a scale factor of 4 and produce a reflection about the horizontal axis? Show that the matrix you came up with combines these two matrices.
Answer:
Yes, by using the matrix \(\left(\begin{array}{cc}
4 & 0 \\
0 & -4
\end{array}\right)\)

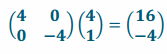
The dilation matrix was \(\left(\begin{array}{ll}
4 & 0 \\
0 & 4
\end{array}\right)\). The rotation matrix was \(\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\). The product of these matrices gives the matrix that produces a dilation and then a rotation.

→ How did you come up with the dilation matrix?
→ I know that a dilation matrix is in the form \(\left(\begin{array}{ll}
k & 0 \\
0 & k
\end{array}\right)\) where k the scale factor is.
→ How did you come up with the reflection matrix?
→ I know that the matrix \(\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\) reflects coordinates about the horizontal axis.
→ How did you come up with a matrix that was both a dilation and a reflection?
→ I knew that I wanted to multiply both the x and y by a factor of 4 and that I also wanted to multiply the y by -1; from that, I combined the two matrices to get \(\left(\begin{array}{cc}
4 & 0 \\
0 & -4
\end{array}\right)\).
→ In what sense did we combine the two matrices?
→ We multiplied 4×-1.
→ We know that transformations are produced through matrix multiplication. What if we have more than one transformation? Could we multiply the two transformation matrices together first instead of completing the transformations in two separate steps?
Write this on the board:

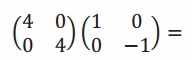
This should be equivalent to applying the dilation and then the reflection. So, what should the product equal?
→ \(\left(\begin{array}{cc}
4 & 0 \\
0 & -4
\end{array}\right)\)

Exercises 1– 3

Exercise 1.
Let I=\(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) and M=\(\left(\begin{array}{ll}
4 & -6 \\
3 & -2
\end{array}\right)\).
a. Find IM.
Answer:
\(\left(\begin{array}{ll}
4 & -6 \\
3 & -2
\end{array}\right)\)

b. Find MI.
Answer:
\(\left(\begin{array}{ll}
4 & -6 \\
3 & -2
\end{array}\right)\)

c. Do these results make sense based on what you know about the matrix \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)?
Answer:
Yes, the matrix \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) is the identity matrix. It corresponds to a transformation that leaves points alone. Therefore, geometrically we must have IM=MI=M.

Exercise 2.
Calculate AB and then BA. Is matrix multiplication commutative?
a. A=\(\left(\begin{array}{cc}
2 & 0 \\
-2 & 3
\end{array}\right)\),B=\(\left(\begin{array}{ll}
1 & 5 \\
0 & 1
\end{array}\right)\)
Answer:

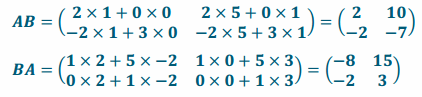
AB≠BA; matrix multiplication is not commutative.

b. A=\(\left(\begin{array}{cc}
-10 & 1 \\
3 & 7
\end{array}\right)\),B=\(\left(\begin{array}{cc}
-3 & 2 \\
4 & -1
\end{array}\right)\)
Answer:

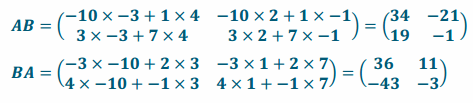
AB≠BA; matrix multiplication is not commutative.

Exercise 3.
Write a matrix that would perform the following transformations in this order: a rotation of 180°, a dilation by a scale factor of 4, and a reflection across the horizontal axis. Use the point \(\left(\begin{array}{l}
2 \\
1
\end{array}\right)\) to illustrate that your matrix is correct.
Answer:

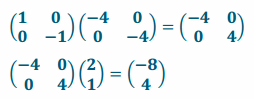
Example 2.
More Operations on Matrices

Find the sum. \(\left(\begin{array}{cc}
2 & 0 \\
-2 & 3
\end{array}\right)\)+\(\left(\begin{array}{ll}
1 & 5 \\
0 & 1
\end{array}\right)\)
Answer:

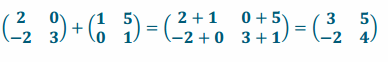
Find the difference. \(\left(\begin{array}{cc}
2 & 0 \\
-2 & 3
\end{array}\right)\)–\(\left(\begin{array}{ll}
1 & 5 \\
0 & 1
\end{array}\right)\)
Answer:

Find the sum. \(\left(\begin{array}{cc}
2 & 0 \\
-2 & 3
\end{array}\right)\)+\(\left(\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right)\)
Answer:

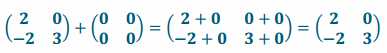
Exercises 4–5

Exercise 4.
Express each of the following as a single matrix.
a. \(\left(\begin{array}{cc}
6 & -3 \\
10 & -1
\end{array}\right)\)+\(\left(\begin{array}{cc}
-2 & 8 \\
3 & -12
\end{array}\right)\)
Answer:
\(\left(\begin{array}{cc}
4 & 5 \\
13 & -13
\end{array}\right)\)

b. \(\left(\begin{array}{ll}
-2 & 7 \\
-3 & 1
\end{array}\right)\left(\begin{array}{l}
3 \\
4
\end{array}\right)\)+\(\left(\begin{array}{l}
1 \\
5
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
23 \\
0
\end{array}\right)\)

c. \(\left(\begin{array}{cc}
8 & 5 \\
0 & 15
\end{array}\right)\) – \(\left(\begin{array}{cc}
4 & -6 \\
-3 & 18
\end{array}\right)\)
Answer:
\(\left(\begin{array}{ll}
4 & 11 \\
3 & -3
\end{array}\right)\)

Exercise 5.
In arithmetic, the additive identity says that for some number a, a+0=0+a=0. What would be an additive identity in matrix arithmetic?
Answer:
We would use the zero matrix. \(\left(\begin{array}{ll}
a & c \\
b & d
\end{array}\right)\)+\(\left(\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right)\)=\(\left(\begin{array}{ll}
a & c \\
b & d
\end{array}\right)\)

Eureka Math Precalculus Module 1 Lesson 25 Problem Set Answer Key

Question 1.
What type of transformation is shown in the following examples? What is the resulting matrix?

a. \(\left(\begin{array}{cc}
\cos (\pi) & -\sin (\pi) \\
\sin (\pi) & \cos (\pi)
\end{array}\right)\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
Answer:
It is a pure rotation. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is rotated π radians, and the image is \(\left(\begin{array}{l}
3 \\
-2
\end{array}\right)\).

b. \(\left(\begin{array}{cc}
0 & -1 \\
1 & 0
\end{array}\right)\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
Answer:
It is a pure rotation. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is rotated \(\frac{π}{2}\) radians, and the image is \(\left(\begin{array}{l}
-2 \\
3
\end{array}\right)\).

c. \(\left(\begin{array}{ll}
3 & 0 \\
0 & 3
\end{array}\right)\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
Answer:
It is dilation with a factor of 3. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is dilated by a factor of 3, and the image is \(\left(\begin{array}{l}
9 \\
6
\end{array}\right)\).

d. \(\left(\begin{array}{cc}
-1 & 0 \\
0 & 1
\end{array}\right)\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
Answer:
It is a reflection about the y-axis. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is reflected about the y-axis, and the image is \(\left(\begin{array}{l}
-3 \\
2
\end{array}\right)\).

e. \(\left(\begin{array}{cc}
1 & 0 \\
0 & -1
\end{array}\right)\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
Answer:
It is a reflection about the x-axis. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is reflected about the x-axis, and the image is \(\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\).

f.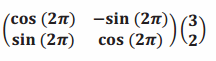
Answer:
It is a pure rotation. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is rotated 2π radians, and the image is \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\).

g.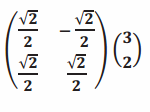
Answer:
It is a pure rotation. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is rotated \(\frac{\pi}{4}\) radians, and the image is \(\left(\begin{array}{c}
\frac{\sqrt{2}}{2} \\
\frac{5 \sqrt{2}}{2}
\end{array}\right)\).

h.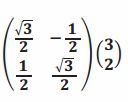
Answer:
It is a pure rotation. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is rotated \(\frac{\pi}{6}\) radians, and the image is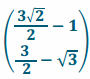

Question 2.
Calculate each of the following products.
a. \(\left(\begin{array}{ll}
2 & 3 \\
5 & 4
\end{array}\right)\left(\begin{array}{l}
2 \\
3
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
13 \\
22
\end{array}\right)\)

b. \(\left(\begin{array}{ll}
3 & 2 \\
4 & 5
\end{array}\right)\left(\begin{array}{ll}
3 & 2 \\
1 & 0
\end{array}\right)\)
Answer:
\(\left(\begin{array}{ll}
11 & 6 \\
17 & 8
\end{array}\right)\)

c. \(\left(\begin{array}{ll}
-1 & -3 \\
-2 & -4
\end{array}\right)\left(\begin{array}{l}
-3 \\
-1
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
6 \\
10
\end{array}\right)\)

d. \(\left(\begin{array}{ll}
-3 & -1 \\
-4 & -2
\end{array}\right)\left(\begin{array}{cc}
-2 & -1 \\
0 & -3
\end{array}\right)\)
Answer:
\(\left(\begin{array}{cc}
6 & 6 \\
8 & 10
\end{array}\right)\)

e. \(\left(\begin{array}{cc}
5 & 0 \\
-1 & 2
\end{array}\right)\left(\begin{array}{l}
0 \\
3
\end{array}\right)\)
Answer:
\(\left(\begin{array}{l}
0 \\
6
\end{array}\right)\)

f. \(\left(\begin{array}{ll}
3 & -1 \\
4 & -2
\end{array}\right)\left(\begin{array}{cc}
1 & 0 \\
-2 & -3
\end{array}\right)\)
Answer:
\(\left(\begin{array}{ll}
5 & 3 \\
8 & 6
\end{array}\right)\)

Question 3.
Calculate each sum or difference.
a. \(\left(\begin{array}{ll}
1 & 3 \\
2 & 4
\end{array}\right)\) + \(\left(\begin{array}{ll}
4 & 2 \\
3 & 1
\end{array}\right)\)
Answer:
\(\left(\begin{array}{ll}
5 & 5 \\
5 & 5
\end{array}\right)\)

b. \(\left(\begin{array}{ll}
-4 & -5 \\
-6 & -7
\end{array}\right)\) + \(\left(\begin{array}{ll}
-2 & 3 \\
-1 & 4
\end{array}\right)\)
Answer:
\(\left(\begin{array}{ll}
-6 & -2 \\
-7 & -3
\end{array}\right)\)

c. \(\left(\begin{array}{c}
-5 \\
4
\end{array}\right)\) + \(\left(\begin{array}{c}
3 \\
2
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
-2 \\
6
\end{array}\right)\)

d. \(\left(\begin{array}{c}
3 \\
-5
\end{array}\right)\) – \(\left(\begin{array}{c}
7 \\
9
\end{array}\right)\)
Answer:
\(\left(\begin{array}{c}
-4 \\
-14
\end{array}\right)\)

e. \(\left(\begin{array}{ll}
-4 & -5 \\
-6 & -7
\end{array}\right)-\left(\begin{array}{ll}
-2 & 3 \\
-1 & 4
\end{array}\right)\)
Answer:
\(\left(\begin{array}{cc}
-2 & -8 \\
-5 & -11
\end{array}\right)\)

Question 4.
In video game programming, Fahad translates a car, whose coordinate is \(\left(\begin{array}{l}
1 \\
1
\end{array}\right)\), 2 units up and 4 units to the right, rotates it \(\frac{π}{2}\) radians counterclockwise, reflects it about the x-axis, reflects it about the y-axis, rotates it \(\frac{π}{2}\) radians counterclockwise, and finally translates it 4 units down and 2 units to the left. What point represents the final location of the car?
Answer:

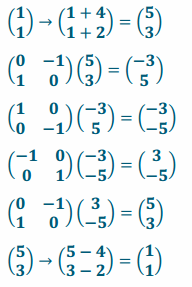
The final location of the car is its initial starting point.

Eureka Math Precalculus Module 1 Lesson 25 Exit Ticket Answer Key

Question 1.
Carmine has never seen matrices before but must quickly understand how to add, subtract, and multiply matrices. Explain the following problems to Carmine.
a.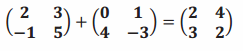
Answer:
To add matrices, add the corresponding elements. So, add the 2 and the 0 because they are both in the first row, first column.

b.
Answer:
To subtract matrices, subtract the corresponding elements. So, subtract the 0 from the 2 because they are both in the first row, first column.

c.
Answer:
To multiply matrices, multiply the elements in the first row by the elements in the first column, and then add the products together.

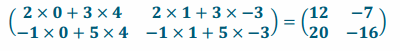
Question 2.
Explain to Carmine the significance of the zero matrix and the multiplicative identity matrix.
Answer:
The zero matrix is \(\left(\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right)\) and is similar to 0 in the real number system. Any matrix added to the zero matrix is itself, and any matrix multiplied by the zero matrix has all terms of 0.
The multiplicative identity matrix is \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) and is similar to 1 in the real number system. Any matrix times the multiplicative identity matrix has a product of itself.