Eureka Math Precalculus Module 1 Lesson 24 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 24 Answer Key

Eureka Math Precalculus Module 1 Lesson 24 Example Answer Key

Example 1.
Determine the following:
a.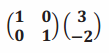
Answer:
\(\left(\begin{array}{c}
3 \\
-2
\end{array}\right)\)

b.
Answer:
\(\left(\begin{array}{c}
-7 \\
12
\end{array}\right)\)

c.
Answer:
\(\left(\begin{array}{cc}
3 & 5 \\
-2 & 1
\end{array}\right)\)

d.
Answer:
\(\left(\begin{array}{cc}
-1 & -3 \\
-7 & 6
\end{array}\right)\)

e.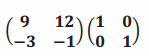
Answer:
\(\left(\begin{array}{cc}
9 & 12 \\
-3 & -1
\end{array}\right)\)

f.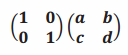
Answer:
\(\left(\begin{array}{ll}
\mathbf{a} & \mathbf{b} \\
\mathbf{c} & \mathbf{d}
\end{array}\right)\)

g.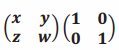
Answer:
\(\left(\begin{array}{cc}
\mathbf{x} & \mathbf{y} \\
\mathbf{z} & \mathbf{w}
\end{array}\right)\)

→ What did you notice about the result of each matrix multiplication problem?
→ The result was always one of the matrices.
→ Which matrix?
→ The one that was not \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)
→ What is this similar to in the real number system?
→ When we multiply by the number 1
→ What do we call the number 1 when multiplying real numbers? Explain.
→ The multiplicative identity because you always get the number that was multiplied by 1 as the product.
→ Can you predict what we call the matrix \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\)?
→ The multiplicative identity matrix
→ Explain to your neighbor what the multiplicative identity matrix is and why it is called the multiplicative identity.
→ Students explain.

Example 2.
Can the reflection about the real axis L(z)=\(\overline{\boldsymbol{Z}}\) be expressed in matrix notation?
Answer:
Yes, using the matrix

→ Is the matrix you found in the same form as those studied in the previous lessons, \(\left(\begin{array}{cc}
a & -b \\
b & a
\end{array}\right)\)?
→ No
→ How did you verify that the matrix you found did in fact produce a reflection about the real axis?
→ I multiplied it by a sample point to see if it reflected the point about the real axis. Teacher note: Allow students to share various responses, even incorrect ones, until the class comes to a consensus on the correct answer.
→ Do you think all matrices in the form \(\left(\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right)\) correspond to a transformation of some kind?
→ Yes, multiplying \(\left(\begin{array}{ll}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{array}\right)\) times some point \(\left(\begin{array}{l}
x \\
y
\end{array}\right)\) will affect the point in some way, thereby producing a transformation of some sort.

Eureka Math Precalculus Module 1 Lesson 24 Exercise Answer Key

Exercises

Exercise 1.
Express a reflection about the vertical axis in matrix notation. Prove that it produces the desired reflection by using matrix multiplication.
Answer:

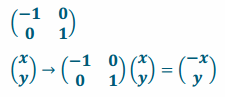
Exercise 2.
Express a reflection about both the horizontal and vertical axes in matrix notation. Prove that it produces the desired reflection by using matrix multiplication.
Answer:

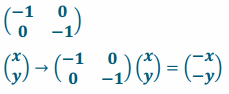
Exercise 3.
Express a reflection about the vertical axis and a dilation with a scale factor of 6 in matrix notation. Prove that it produces the desired reflection by using matrix multiplication.
Answer:

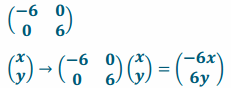
→ For Exercise 2, could this transformation also be viewed as a rotation?
→ Yes. Reflecting about both axes is the same as a 180° rotation.
→ Is it possible to have a dilation where the x-coordinate is increased by a different scale factor than the
y-coordinate?
→ Yes. For example, \(\left(\begin{array}{ll}
2 & 0 \\
0 & 3
\end{array}\right)\) would dilate the x by a factor of 2 and the y by a factor of 3.

Explore the transformation given by each matrix below. Use the graph of the rectangle provided to assist in the exploration. Describe the effect on the graph of the rectangle, and then show the general effect of the transformation by using matrix multiplication.


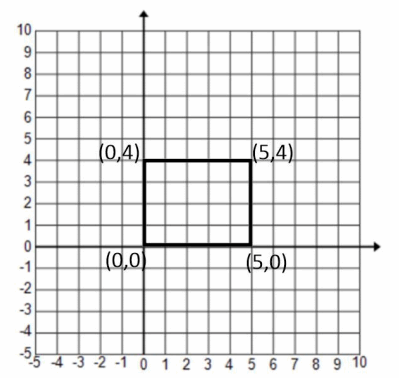
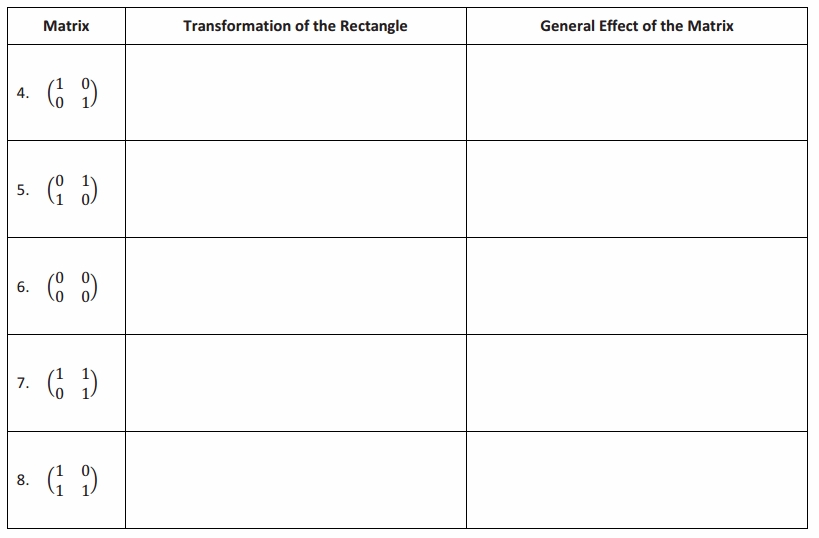
Answer:

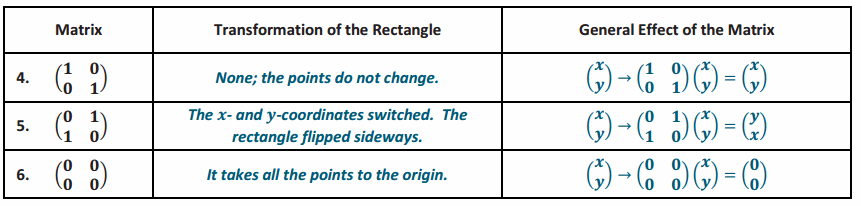
→ What effect did the matrix \(\left(\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right)\) have on the graph?
→ None
→ This is called an identity matrix because it is equivalent to multiplying by 1.
→ Is the matrix \(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\) also an identity matrix?
→ No. It did change the coordinates. Teacher note: The teacher may demonstrate or lead students to the fact that the graph was reflected about the line y=x, but it is not the focal point of this lesson.
→ Can we view the zero matrix \(\left(\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right)\) as a dilation?
→ Yes, with a scale factor of 0
→ How would you classify the last two transformations?
→ It was sort of like a translation because some of the points moved to the right, but some of them remained fixed. It does not exactly fit into any of our transformations. Teacher note: These are both examples of shears, but the main point is that all of these matrices produce some sort of transformation but not necessarily ones that we know about at this point.

Eureka Math Precalculus Module 1 Lesson 24 Problem Set Answer Key

Question 1.
What matrix do you need to use to reflect the following points about the y-axis? What is the resulting matrix when this is done? Show all work and sketch it.
a. \(\left(\begin{array}{l}
3 \\
0
\end{array}\right)\)
Answer:

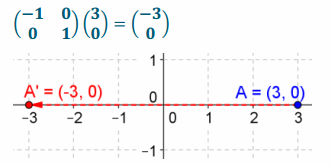
b. \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\)
Answer:

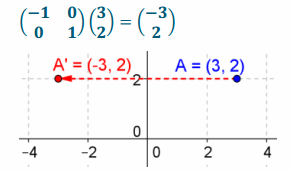
c. \(\left(\begin{array}{l}
-4 \\
3
\end{array}\right)\)
Answer:

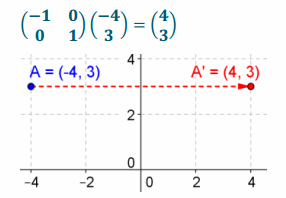
d. \(\left(\begin{array}{c}
-3 \\
-2
\end{array}\right)\)
Answer:

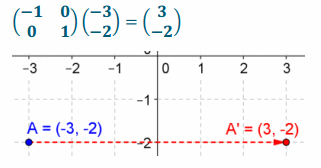
e. \(\left(\begin{array}{c}
3 \\
-3
\end{array}\right)\)
Answer:

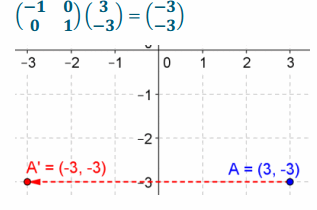
f. \(\left(\begin{array}{c}
5 \\
4
\end{array}\right)\)
Answer:

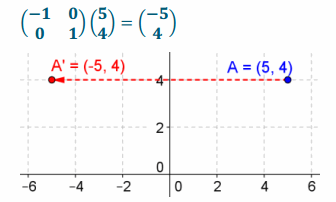
Question 2.
What matrix do you need to use to reflect the following points about the x-axis? What is the resulting matrix when this is done? Show all work and sketch it.

a. \(\left(\begin{array}{c}
0 \\
3
\end{array}\right)\)
Answer:

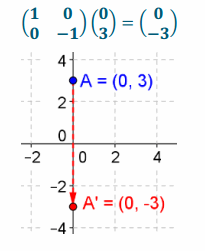
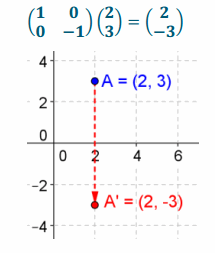
b. \(\left(\begin{array}{c}
2 \\
3
\end{array}\right)\)
Answer:

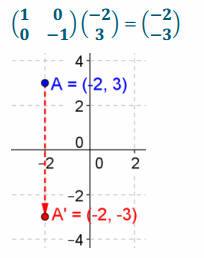
c. \(\left(\begin{array}{c}
-2 \\
3
\end{array}\right)\)
Answer:

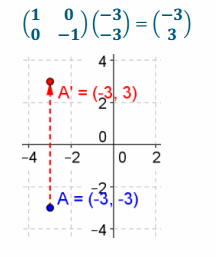
d. \(\left(\begin{array}{c}
-3 \\
-3
\end{array}\right)\)
Answer:

e. \(\left(\begin{array}{c}
3 \\
-3
\end{array}\right)\)
Answer:

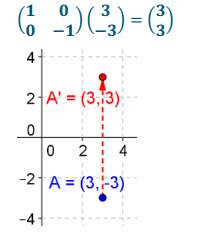
f. \(\left(\begin{array}{c}
-3 \\
4
\end{array}\right)\)
Answer:

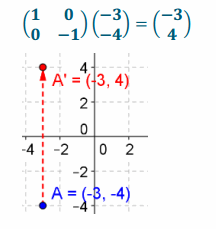
Question 3.
What matrix do you need to use to dilate the following points by a given factor? What is the resulting matrix when this is done? Show all work and sketch it.
a. \(\left(\begin{array}{c}
1 \\
0
\end{array}\right)\), a factor of 3
Answer:

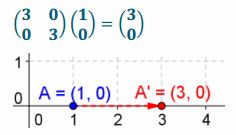
b. \(\left(\begin{array}{c}
3 \\
2
\end{array}\right)\), a factor of 2
Answer:

c. \(\left(\begin{array}{c}
1 \\
-2
\end{array}\right)\), a factor of 1
Answer:

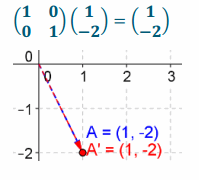
d. \(\left(\begin{array}{c}
-4 \\
-6
\end{array}\right)\), a factor of \(\frac{1}{2}\)
Answer:

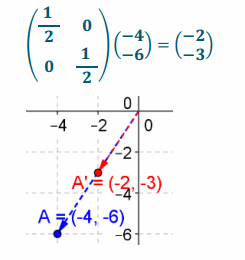
e. (\(\left(\begin{array}{c}
9 \\
3
\end{array}\right)\)), a factor of \(\frac{1}{3}\)
Answer:

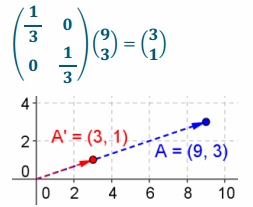
f. \(\left(\begin{array}{l}
\sqrt{3} \\
\sqrt{11}
\end{array}\right)\), a factor of \(\sqrt{2}\)
Answer:

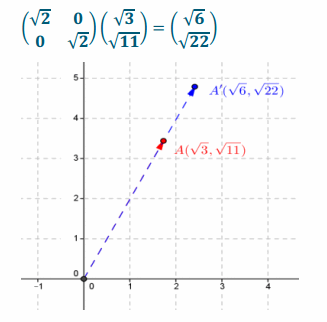
Question 4.
What matrix will rotate the given point by the angle? What is the resulting matrix when this is done? Show all work and sketch it.
a. \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\), \(\frac{π}{2}\) radians
Answer:

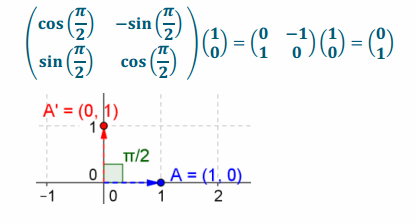
b. \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\)
Answer:

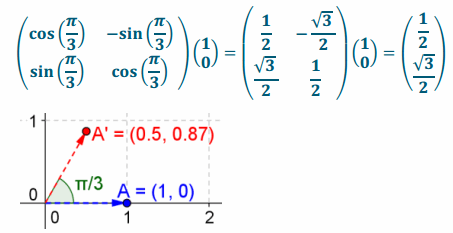
c. (\(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\)), \(\frac{\pi}{6}\) radians
Answer:

d. \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\), \(\frac{\pi}{4}\) radians
Answer:

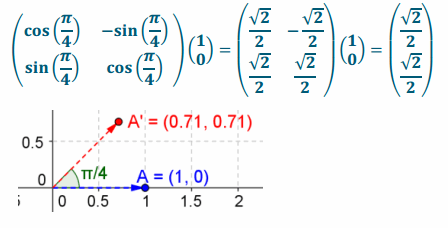
e. \(\left(\begin{array}{l}
\frac{\sqrt{3}}{2} \\
\frac{1}{2}
\end{array}\right)\), \(\frac{\pi}{6}\) radians
Answer:

f. (\(\left(\begin{array}{c}
\frac{\sqrt{2}}{2} \\
\frac{\sqrt{2}}{2}
\end{array}\right)\)), \(\frac{\pi}{4}\) radians
Answer:

g. \(\left(\begin{array}{c}
\frac{\sqrt{3}}{2} \\
\frac{1}{2}
\end{array}\right)\), π radians
Answer:

h. \(\left(\begin{array}{l}
1 \\
0
\end{array}\right)\), –\(\frac{\pi}{6}\) radians
Answer:

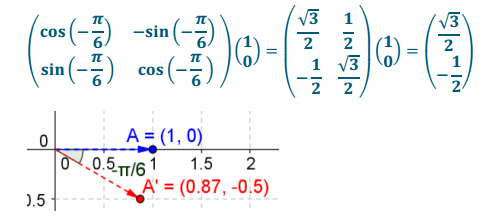
Question 5.
For the transformation shown below, find the matrix that will transform point A to A’, and verify your answer.
Answer:
A=(2,1),OA=\(\sqrt{(2)^{2}+(1)^{2}}\)=\(\sqrt{5}\)
A’=(-2,4),OA=\(\sqrt{(-2)^{2}+(4)^{2}}\)=\(\sqrt{20}\)=2\(\sqrt{5}\); therefore, it has a dilation of 2.

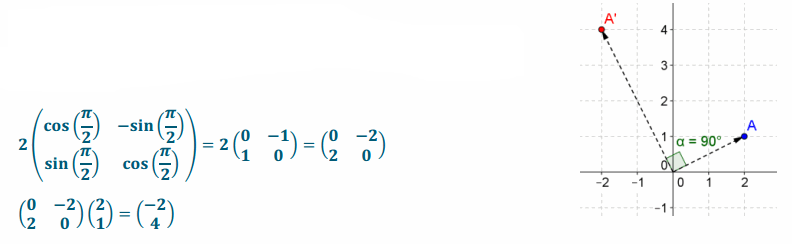
Question 6.
In this lesson, we learned \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right]\) will produce a reflection about the line y=x. What matrix will produce a reflection about the line y=-x? Verify your answers by testing the given point \(\left(\begin{array}{l}
3 \\
1
\end{array}\right)\) and graphing them on the coordinate plane.
Answer:

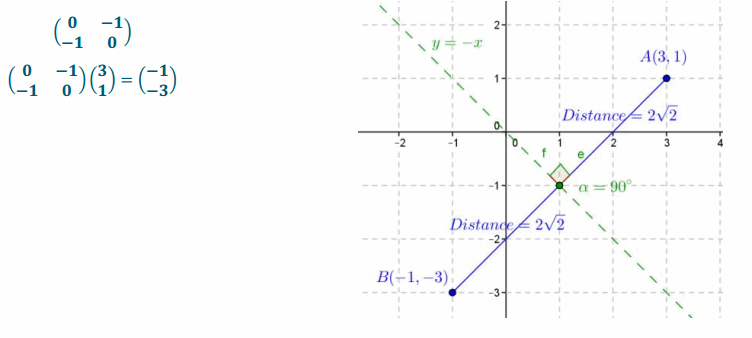
Question 7.
Describe the transformation and the translations in the diagram below. Write the matrices that will perform the tasks. What is the area that these transformations and translations have enclosed?
Answer:
First, A is rotated a π radian counterclockwise to A’; next, it is translated to A”; finally, it is translated back to A.

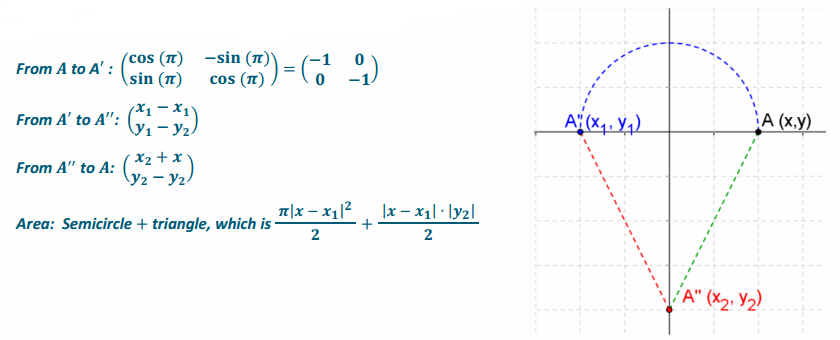
Question 8.
Given the kite figure ABCD below, answer the following questions.
Answer:

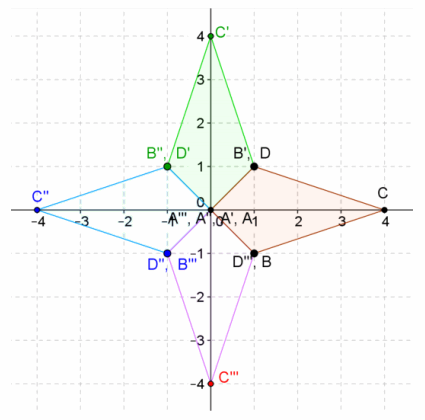
a. Explain how you would create the star figure above using only rotations.
Answer:
By rotating the kite figure ABCD \(\frac{π}{2}\) radians counterclockwise or clockwise four times

b. Explain how to create the star figure above using reflections and rotation.
Answer:
Answers will vary. One explanation is to rotate the kite figure ABCD \(\frac{π}{2}\) radians counterclockwise to get to A’B’C’D’ and then reflect both figures about the line y=-x, which is .

c. Explain how to create the star figure above using only reflections. Explain your answer.
Answer:
First, reflect the kite figure ABCD about the line y=x, which is \(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\); then, reflect A’B’C’D’ about the line y=-x, which is \(\left(\begin{array}{cc}
0 & -1 \\
-1 & 0
\end{array}\right)\); next, reflect A”B”C”D” about the line y=x, which is \(\left(\begin{array}{ll}
0 & 1 \\
1 & 0
\end{array}\right)\); finally, reflect A”’B”’C”’D”’ about the line y=-x, which is \(\left(\begin{array}{cc}
0 & -1 \\
-1 & 0
\end{array}\right)\).

Question 9.
Given the rectangle ABCD below, answer the following questions.
Answer:

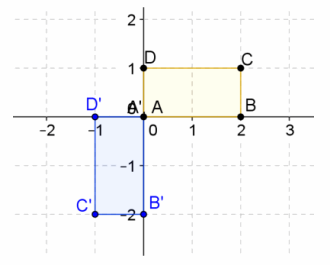
a. Can you transform the rectangle A’B’C’D’ above using only rotations? Explain your answer.
Answer:
No, because no matter how it is rotated, the vertices of the rectangle will not stay the same with respect to each other.

b. Describe a way to create the rectangle A’B’C’D’.
Answer:
Answers will vary. One way is to reflect the rectangle ABCD about the y-axis first, which is , and then rotate \(\frac{π}{2}\) radians counterclockwise, which is .

c. Can you make the rectangle A’B’C’D’ above using only reflections? Explain your answer.
Answer:
Yes, reflect the rectangle ABCD about the line y=-x, which is \(\left(\begin{array}{cc}
0 & -1 \\
-1 & 0
\end{array}\right)\).

Eureka Math Precalculus Module 1 Lesson 24 Exit Ticket Answer Key

What type of transformation is shown in the following examples? What is the resulting matrix?

Question 1.

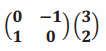
Answer:
It is a pure rotation. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is rotated \(\frac{π}{2}\) radians, and the image is \(\left(\begin{array}{c}
-2 \\
3
\end{array}\right)\).

Question 2.

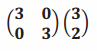
Answer:
It is dilation with a factor of 3. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is dilated by a factor of 3, and the image is \(\left(\begin{array}{l}
9 \\
6
\end{array}\right)\).

Question 3.

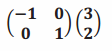
Answer:
It is a reflection about the y-axis. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is reflected about the y-axis, and the image is \(\left(\begin{array}{l}
-3 \\
2
\end{array}\right)\).

Question 4.

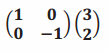
Answer:
It is a reflection about the x-axis. The point \(\left(\begin{array}{l}
3 \\
2
\end{array}\right)\) is reflected about the x-axis, and the image is \(\left(\begin{array}{l}
3 \\
-2
\end{array}\right)\).

Question 5.
What is the multiplicative identity matrix? What is it similar to in the set of real numbers? Explain your answer.
Answer:
The multiplicative identity matrix is \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\). It is similar to the number 1 in the real number system because any matrix multiplied by \(\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\) produces the original matrix.