Eureka Math Precalculus Module 1 Lesson 18 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 18 Answer Key

Eureka Math Precalculus Module 1 Lesson 18 Exercise Answer Key

Opening Exercise

Identify the modulus and argument of each complex number, and then rewrite it in rectangular form.

i. 2(cos⁡($\frac{π}{4}$) + i sin⁡($\frac{π}{4}$) )
Answer:
The modulus is 2, and the argument is $\frac{π}{4}$. The number is $\sqrt{2}$ + i$\sqrt{2}$.

ii. 5(cos⁡($\frac{2π}{3}$) + i sin⁡($\frac{2π}{3}$) )
Answer:
The modulus is 5, and the argument is $\frac{2π}{3}$. The number is – $\frac{5}{2}$ + i$\frac{5 \sqrt{3}}{2}$.

iii. 3$\sqrt{2}$ (cos⁡($\frac{7π}{4}$) + i sin⁡($\frac{7π}{4}$) )
Answer:
The modulus is 3$\sqrt{2}$, and the argument is $\frac{7π}{4}$. The number is 3 – 3i.

iv. 3(cos⁡($\frac{7π}{6}$) + i sin⁡($\frac{7π}{6}$) )
Answer:
The modulus is 3, and the argument is $\frac{7π}{6}$. The number is – $\frac{3 \sqrt{3}}{2}$ – $\frac{3}{2}$i.

v. 1(cos⁡(π) + i sin⁡(π) )
Answer:
The modulus is 1, and the argument is π. The number is – 1.

b. What is the argument and modulus of each complex number? Explain how you know.
i. 2 – 2i
Answer:
We have |2 – 2i|= 2$\sqrt{2}$, and arg⁡(2 – 2i)= $\frac{7π}{4}$. The point (2, – 2) is located in the fourth quadrant. The ray from the origin containing the point is a rotation of $\frac{7π}{4}$ from the ray through the origin containing the real number 1.

ii. 3$\sqrt{3}$ + 3i
Answer:
We have |3$\sqrt{3}$ + 3i|= 6, and arg⁡(3$\sqrt{3}$ + 3i)= $\frac{π}{6}$. The point (3$\sqrt{3}$,3) is located in the first quadrant. The ray from the origin containing the point is a rotation of $\frac{π}{6}$ from the ray through the origin containing the real number 1.

iii. – 1 – $\sqrt{3}$i
Answer:
We have | – 1 – $\sqrt{3}$i|= 2, and arg⁡( – 1 – $\sqrt{3}$i)= $\frac{4π}{3}$. The point ( – 1, – $\sqrt{3}$) is located in the third quadrant. The ray from the origin containing the point is a rotation of $\frac{4π}{3}$ from the ray through the origin containing the real number 1.

iv. – 5i
Answer:
We have | – 5i|= 5, and arg⁡( – 5i)= $\frac{3π}{2}$. The point (0, – 5) is located on the imaginary axis. The ray from the origin containing the point is a rotation of $\frac{3π}{2}$ from the ray through the origin containing the real number 1.

v. 1
Answer:
We have |1|= 1, and arg⁡(1)= 0. This is the real number 1.

Exploratory Challenge/Exercises 1–12 (20 minutes)

Students investigate and ultimately generalize a formula for quickly calculating the value of zⁿ. The class should work on these problems in teams of three to four students each. Use the discussion questions to help move individual groups forward as they work through the exercises in this exploration. Each group should have graph paper for each group member and access to a calculator to check calculations if needed.

In Exercise 3, most groups probably expand the number and perform the calculation in rectangular form. Here polar form offers little advantage. Perhaps when the exponent is a 4, a case could be made that polar form is more efficient for calculating a power of a complex number.
Be sure to pause and debrief with the entire class after Exercise 5. All students need to have observed the patterns in the table in order to continue to make progress discovering the relationships about powers of a complex number.

Exploratory Challenge/Exercises 1–12

Exercise 1.
Rewrite each expression as a complex number in rectangular form.
a. (1 + i)²
Answer:
(1 + i)(1 + i)= 1 + 2i + i²= 1 + 2i – 1= 2i

b. (1 + i)³
Answer:
(1 + i)³= (1 + i)² (1 + i)= 2i(1 + i)= 2i + 2i²= – 2 + 2i

c. (1 + i)⁴
Answer:
(1 + i)⁴= (1 + i)² (1 + i)²= 2i∙2i= 4i²= – 4

Exercise 2.
Complete the table below showing the rectangular form of each number and its modulus and argument.
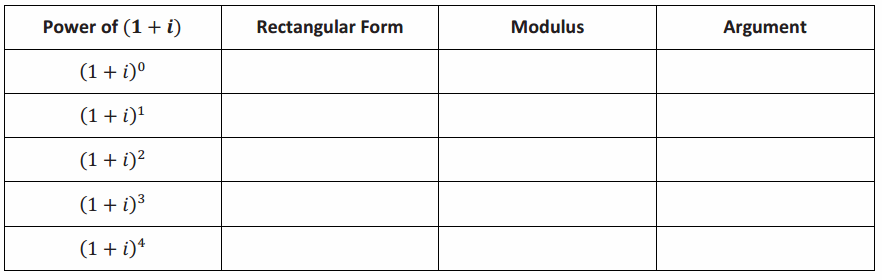
$Eureka Math Precalculus Module 1 Lesson 18 Exercise Answer Key 10$
Answer:
$Eureka Math Precalculus Module 1 Lesson 18 Exercise Answer Key 11$

Exercise 3.
What patterns do you notice each time you multiply by another factor of (1 + i)?
Answer:
The argument increases by $\frac{π}{4}$. The modulus is multiplied by $\sqrt{2}$.

Before proceeding to the rest of the exercises in this Exploratory Challenge, check to make sure each group observed the patterns in the table required for them to make the connection that repeatedly multiplying by the same complex number causes repeated rotation by the argument, dilation, and modulus of the number.
Debrief the first five exercises by having one or two groups present their findings on the board or document camera.

Exercise 4.
Graph each power of 1 + i shown in the table on the same coordinate grid. Describe the location of these numbers in relation to one another using transformations.
Answer:
Starting with (1 + i)⁰, each subsequent complex number is a 45° rotation and a dilation by a factor of $\sqrt{2}$ of the previous one. The graph shows the graphs of z_n= (1 + i)ⁿ for n= 0,1,2,3,4,5.
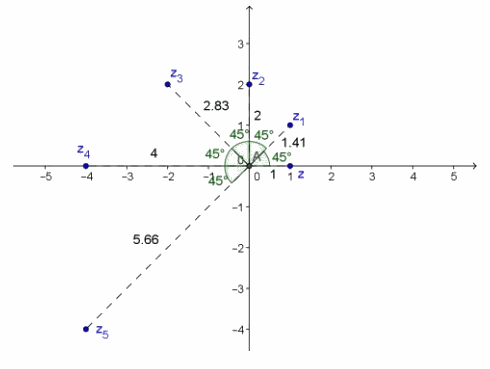
$Eureka Math Precalculus Module 1 Lesson 18 Exercise Answer Key 35$

Exercise 5.
Predict what the modulus and argument of (1 + i)⁵ would be without actually performing the multiplication. Explain how you made your prediction.
Answer:
The modulus would be 4$\sqrt{2}$, and the argument would be π + $\frac{π}{4}$= $\frac{5π}{4}$.

Exercise 6.
Graph (1 + i)⁵ in the complex plane using the transformations you described in Exercise 5.
Answer:
See the solution to Exercises 4 and 5.

Exercise 7.
Write each number in polar form using the modulus and argument you calculated in Exercise 4.
(1 + i)⁰=
(1 + i)¹=
(1 + i)²=
(1 + i)³=
(1 + i)⁴=
Answer:
(1 + i)⁰= 1(cos⁡(0) + i sin⁡(0))
(1 + i)¹= $\sqrt{2}$ (cos⁡($\frac{π}{4}$) + i sin⁡($\frac{π}{4}$) )
(1 + i)²= 2(cos⁡($\frac{π}{2}$) + i sin⁡($\frac{π}{2}$) )
(1 + i)³= 2$\sqrt{2}$ (cos⁡(3$\frac{π}{4}$) + i sin⁡(3$\frac{π}{4}$) )
(1 + i)⁴= 4(cos⁡(π) + i sin⁡(π) )

Exercise 8.
Use the patterns you have observed to write (1 + i)⁵ in polar form, and then convert it to rectangular form.
Answer:
(1 + i)⁵= 4$\sqrt{2}$ (cos⁡($\frac{5π}{4}$) + i sin⁡($\frac{5π}{4}$) )

Exercise 9.
What is the polar form of (1 + i)²⁰? What is the modulus of (1 + i)²⁰? What is its argument? Explain why (1 + i)²⁰ is a real number.
Answer:
In polar form, the number would be ($\sqrt{2}$)²⁰ (cos⁡(20∙$\frac{π}{4}$) + i sin⁡(20∙$\frac{π}{4}$) ). The modulus is ($\sqrt{2}$)²⁰= 2¹⁰= 1024.
The argument is the rotation between 0 and 2π that corresponds to a rotation of 20∙$\frac{π}{4}$= 5π. The argument is π. This rotation takes the number 1 to the negative real – axis and dilates it by a factor of 1,024, resulting in the number – 1,024, which is a real number.

Pause here to discuss the advantages of considering the geometric effect of multiplication by a complex number when raising a complex number to a large integer exponent. Lead a discussion so students understand that the polar form of a complex number makes this type of multiplication very efficient.

→ How do you represent multiplication by a complex number when written in polar form?
→ The product of two complex numbers has a modulus that is the product of the two factors’ moduli and an argument that is the sum of the two factors’ arguments.
→ How does understanding the geometric effect of multiplication by a complex number make solving Exercises 10 and 11 easier than repeatedly multiplying by the rectangular form of the number?
→ If you know the modulus and argument of the complex number, and you want to calculate zⁿ, then the argument will be n times the argument, and the modulus will be the modulus raised to the n.
→ In these exercises, you worked with powers of 1 + i. Do you think the patterns you observed can be generalized to any complex number raised to a positive integer exponent? Explain your reasoning.
→ Since the patterns we observed are based on repeatedly multiplying by the same complex number, and since the geometric effect of multiplication always involves a rotation and dilation, this process should apply to all complex numbers.
→ How can you quickly raise any complex number of a large integer exponent?
→ Determine the modulus and argument of the complex number. Then, multiply the argument by the exponent, and raise the modulus to the exponent. Then, you can write the number easily in polar and then rectangular form.

This exploration largely relies on students using inductive reasoning to observe patterns in powers of complex numbers. The formula they write in Exercise 11 is known as DeMoivre’s formula (or DeMoivre’s theorem). More information and a proof by mathematical induction that this relationship holds can be found at http://en.wikipedia.org/wiki/De_Moivre’s_formula.

If students have been struggling with this exploration, lead a whole – class discussion on the next several exercises, or groups can proceed to work through the rest of this Exploratory Challenge on their own. Be sure to monitor groups, and keep referring them back to the patterns they observed in the tables and graphs as they make their generalizations. Before students begin, announce that they are generalizing the patterns they observed in the previous exercises. Make sure they understand that the goal is a formula or process for quickly raising a complex number to an integer exponent. Observe groups, and encourage students to explain to one another how they are seeing the formula as they work through these exercises.

Exercise 10.
If z has modulus r and argument θ, what are the modulus and argument of z²? Write the number z² in polar form.
Answer:
The modulus would be r², and the argument would be a rotation between 0 and 2π that is equivalent to 2θ.
z²= r² (cos⁡(2θ) + i sin⁡(2θ))

Exercise 11.
If z has modulus r and argument θ, what are the modulus and argument of zⁿ where n is a nonnegative integer? Write the number zⁿ in polar form. Explain how you got your answer.
Answer:
The modulus would be rⁿ, and the argument would be a rotation between 0 and 2π that is equivalent to nθ.
zⁿ= rⁿ (cos⁡(nθ) + i sin⁡(nθ)

Exercise 12.
Recall that $\frac{1}{z}$= $\frac{1}{r}$(cos⁡( – θ) + i sin⁡( – θ)). Explain why it would make sense that the formula holds for all integer values of n.
Answer:
Since $\frac{1}{z}$= z^{– 1}, it would make sense that the formula would hold for negative integers as well. If you plot $\frac{1}{z^{2}}$, $\frac{1}{z^{3}}$, etc., you can see the pattern holds.

In Exercise 14, students must consider why this formula holds for negative integers as well. Ask them how they could verify graphically or algebraically that these formulae could be extended to include negative integer exponents. Consider demonstrating this using graphing software such as Geogebra or Desmos.

Close this section by recording the formula shown below on the board. Ask students to summarize to a partner how to use this formula with the number (1 + i)¹0 and to record it in their notes.

→ Given a complex number z with modulus r and argument θ, the nth power of z is given by zⁿ= rⁿ (cos⁡(nθ) + i sin⁡(nθ)) where n is an integer.

Exercises 13–14

Exercise 13.
Compute $\left(\frac{1 – i}{\sqrt{2}}\right)^{7}$, and write it as a complex number in the form a + bi where a and b are real numbers.
Answer:
The modulus of $\frac{1 – i}{\sqrt{2}}$is 1, and the argument is $\frac{7π}{4}$. The polar form of the number is
1⁷ (cos⁡(7∙$\frac{7π}{4}$) + i sin⁡(7∙$\frac{7π}{4}$) ).
Converting this number to rectangular form by evaluating the sine and cosine values produces $\frac{\sqrt{2}}{2}$ + $\frac{\sqrt{2}}{2}$i.

Exercise 14.
Write (1 + $\sqrt{3}$i)⁶, and write it as a complex number in the form a + bi where a and b are real numbers.
Answer:
The modulus of 1 + $\sqrt{3}$i is 2, and the argument is $\frac{π}{3}$. The polar form of the number is
2⁶ (cos⁡(6∙$\frac{π}{3}$) + i sin⁡(6∙$\frac{π}{3}$) ).
Converting this number to rectangular form by evaluating the sine and cosine values produces
64(1 + 0∙i)= 64.

Eureka Math Precalculus Module 1 Lesson 18 Problem Set Answer Key

Question 1.
Write the complex number in a + bi form where a and b are real numbers.

a. 2(cos⁡($\frac{5π}{3}$) + i sin⁡($\frac{5π}{3}$) )
Answer:
2(cos⁡($\frac{5π}{3}$) + i sin⁡($\frac{5π}{3}$) )= 2($\frac{1}{2}$ – $\frac{\sqrt{3}}{2}$i)
= 1 – $\sqrt{3}$i

b. 3(cos⁡(210°) + i sin⁡(210°) )
Answer:
3(cos⁡(210°) + i sin⁡(210°) )= 3( – $\frac{\sqrt{3}}{2}$ – $\frac{1}{2}$i)
= – $\frac{3 \sqrt{3}}{2}$ – $\frac{3}{2}$i

c. ($\sqrt{2}$)¹⁰ (cos⁡($\frac{15π}{4}$) + i sin⁡($\frac{15π}{4}$))
Answer:
($\sqrt{2}$)¹⁰ (cos⁡($\frac{15π}{4}$) + i sin⁡($\frac{15π}{4}$) ) = 32(cos($\frac{7π}{4}$) + i sin($\frac{7π}{4}$))
= 32($\frac{\sqrt{2}}{2}$ – i$\frac{\sqrt{2}}{2}$)
= 16$\sqrt{2}$ – 16$\sqrt{2}$i

d. cos⁡(9π) + i sin⁡(9π)
Answer:
cos⁡(9π) + i sin⁡(9π)= cos(π) + i sin(π)
= – 1 + 0i
= – 1

e. 4³ (cos⁡($\frac{3π}{4}$) + i sin⁡($\frac{3π}{4}$) )
Answer:
4³ (cos⁡($\frac{3π}{4}$) + i sin⁡($\frac{3π}{4}$) )= 64( – $\frac{\sqrt{2}}{2}$ + i $\frac{\sqrt{2}}{2}$)
= – 32$\sqrt{2}$ + 32$\sqrt{2}$i

f. 6(cos⁡(480°) + i sin⁡(480°) )
Answer:
6(cos⁡(480°) + i sin⁡(480°) )= 6(cos(120°) + i sin(120°))
= 6( – $\frac{1}{2}$ + $\frac{\sqrt{3}}{2}$i)
= – 3 + 3$\sqrt{3}$i

Question 2.
Use the formula discovered in this lesson to compute each power of z. Verify that the formula works by expanding and multiplying the rectangular form and rewriting it in the form a + bi where a and b are real numbers.

a. (1 + $\sqrt{3}$i)³
Answer:
Since z= 1 + $\sqrt{3}$i, we have |z|= $\sqrt{1 + 3}$= 2, and θ= $\frac{π}{3}$. Then,
(1 + $\sqrt{3}$i)³= 2³ (cos(3∙$\frac{π}{3}$) + isin(3∙$\frac{π}{3}$))= 8(cos(π) + isin(π))= – 8
(1 + $\sqrt{3}$i)³= (1 + $\sqrt{3}$i)(1 + 2$\sqrt{3}$i – 3)= (1 + $\sqrt{3}$i)( – 2 + 2$\sqrt{3}$i)= – 2 + 2$\sqrt{3}$i – 2$\sqrt{3}$i – 6= – 8

b. ( – 1 + i)⁴
Answer:
Since z= – 1 + i, we have |z|= $\sqrt{1 + 1}$= $\sqrt{2}$, and θ= 3$\frac{π}{4}$. Then,
( – 1 + i)⁴= ($\sqrt{2}$)⁴ (cos(4∙$\frac{3π}{4}$) + isin(4∙$\frac{3π}{4}$))= 4(cos(3π) + isin(3π))= – 4
( – 1 + i)⁴= ( – 1 + i)² ( – 1 + i)²= (1 – 2i – 1)(1 – 2i – 1)= ( – 2i)( – 2i)= – 4

c. (2 + 2i)⁵
Answer:
Since z= 2 + 2i, we have |z|= $\sqrt{2^{2} + 2^{2}}$= 2$\sqrt{2}$, and θ= $\frac{π}{4}$. Then,
(2 + 2i)⁵= (2$\sqrt{2}$)⁵ (cos(5∙$\frac{π}{4}$) + isin(5∙$\frac{π}{4}$))= 128$\sqrt{2}$ ( – $\frac{\sqrt{2}}{2}$ – $\frac{\sqrt{2}}{2}$i)= – 128 – 128i
(2 + 2i)⁵= (2 + 2i)² (2 + 2i)² (2 + 2i)= (4 + 8i – 4)(4 + 8i – 4)(2 + 2i)= (8i)(8i)(2 + 2i)
= – 64(2 + 2i)= – 128 – 128i

d. (2 – 2i)^{– 2}
Answer:
Since z= 2 – 2i, we have |z|= $\sqrt{2^{2} + 2^{2}}$= 2$\sqrt{2}$, and θ= $\frac{7π}{4}$. Then,
(2 – 2i)^{– 2}= (2$\sqrt{2}$)^{– 2} (cos( – 2∙$\frac{7π}{4}$) + isin( – 2∙$\frac{7π}{4}$))= $\frac{1}{8}$(0 + i)= $\frac{1}{8i}$
(2 – 2i)^{– 2}= $\frac{1}{(2 – 2 i)^{2}}$ = $\frac{1}{4 – 8 i – 4}$= $\frac{1}{ – 8 i}$∙$\frac{i}{\boldsymbol{i}}$= $\frac{i}{8}$= $\frac{1}{8i}$

e. ($\sqrt{3}$ – i)⁴
Answer:
Since z= $\sqrt{3}$ – i, we have |z|= $\sqrt{\sqrt{3}^{2} + 1^{2}}$= 2, and θ= $\frac{11π}{6}$. Then,
($\sqrt{3}$ – i)⁴= 2⁴ (cos(4∙$\frac{11π}{6}$) + isin(4∙$\frac{11π}{6}$))= 16(cos($\frac{22π}{3}$) + isin($\frac{22π}{3}$))= 16( – $\frac{1}{2}$ – $\frac{\sqrt{3}}{2}$i)
= – 8 – 8$\sqrt{3}$i
($\sqrt{3}$ – i)⁴= ($\sqrt{3}$ – i)² ($\sqrt{3}$ – i)²= (3 – 2$\sqrt{3}$i – 1)(3 – 2$\sqrt{3}$i – 1)= (2 – 2$\sqrt{3}$i)(2 – 2$\sqrt{3}$i)
= 4 – 8$\sqrt{3}$i – 12= – 8 – 8$\sqrt{3}$i

f. (3$\sqrt{3}$ – 3i)⁶
Answer:
Since z= 3$\sqrt{3}$ – 3i, we have |z|= $\sqrt{(3 \sqrt{3})^{2} + 3^{2}}$= $\sqrt{36}$= 6, and θ= $\frac{11π}{6}$. Then,
(3$\sqrt{3}$ – 3i)⁶= 6⁶ (cos(6∙$\frac{11π}{6}$) + isin(6∙$\frac{11π}{6}$))= 46656(cos(11π) + isin(11π))= – 46656
(3$\sqrt{3}$ – 3i)⁶= (3$\sqrt{3}$ – 3i)² (3$\sqrt{3}$ – 3i)² (3$\sqrt{3}$ – 3i)²
= (27 – 18$\sqrt{3}$i – 9)(27 – 18$\sqrt{3}$i – 9)(27 – 18$\sqrt{3}$i – 9)
= (18 – 18$\sqrt{3}$i)(18 – 18$\sqrt{3}$i)(18 – 18$\sqrt{3}$i)
= (324 – 648$\sqrt{3}$i – 972)(18 – 18$\sqrt{3}$i)= ( – 648 – 648$\sqrt{3}$i)(18 – 18$\sqrt{3}$i)
= – 11664 + 11664$\sqrt{3}$i – 11664$\sqrt{3}$i – 34992= – 46656

Question 3.
Given z= – 1 – i, graph the first five powers of z by applying your knowledge of the geometric effect of multiplication by a complex number. Explain how you determined the location of each in the coordinate plane.
Answer:
Multiplication by –1 – i will dilate by |–1 – i|= $\sqrt{1 + 1}$= $\sqrt{2}$ and rotate by arg( – 1 – i)= $\frac{5π}{4}$. Then, the graph below shows z= – 1 – i, z²= ( – 1 – i)², z³= ( – 1 – i)³, z⁴= ( – 1 – i)⁴, and z⁵= ( – 1 – i)⁵.
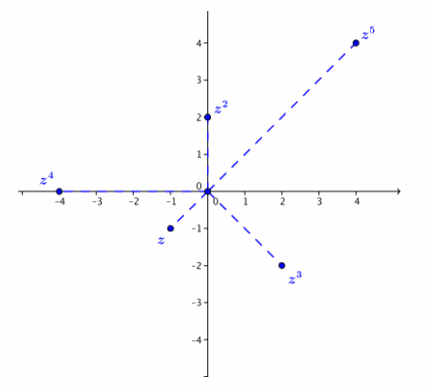
$Engage NY Math Precalculus Module 1 Lesson 18 Problem Set Answer Key 60$
To locate each point, multiply the distance from the previous point to the origin by the modulus ($\sqrt{2}$), and rotate counterclockwise $\frac{5π}{4}$.

Question 4.
Use your work from Problem 3 to determine three values of n for which ( – 1 – i)ⁿ is a multiple of – 1 – i.
Answer:
Since multiplication by – 1 – i rotates the point by $\frac{5π}{4}$ radians, the point ( – 1 – i)ⁿ is a multiple of the original
z= – 1 – i every 8 iterations. Thus, ( – 1 – i)⁹, ( – 1 – i)¹⁷,( – 1 – i)²⁵ are all multiples of (1 – i). Answers will vary.

Question 5.
Find the indicated power of the complex number, and write your answer in form a + bi where a and b are real numbers.
a. [2(cos⁡($\frac{3π}{4}$) + i sin⁡($\frac{3π}{4}$) )]³
Answer:
[2(cos⁡($\frac{3π}{4}$) + i sin⁡($\frac{3π}{4}$) )]³= 2³ (cos(3∙$\frac{3π}{4}$) + isin(3∙$\frac{3π}{4}$))
= 8(cos($\frac{9π}{4}$) + isin($\frac{9π}{4}$))
= 8($\frac{\sqrt{2}}{2}$ + $\frac{\sqrt{2}}{2}$i)
= 4$\sqrt{2}$ + 4$\sqrt{2}$i

b. [$\sqrt{2}$ (cos⁡($\frac{π}{4}$) + i sin⁡($\frac{π}{4}$))]¹⁰
Answer:
[$\sqrt{2}$ (cos⁡($\frac{π}{4}$) + i sin⁡($\frac{π}{4}$) )]¹⁰ = ($\sqrt{2}$)¹⁰(cos($\frac{10π}{4}$) + isin($\frac{10π}{4}$))
= 32(0 + 1i)
= 32i

c. (cos⁡($\frac{5π}{6}$) + i sin⁡($\frac{5π}{6}$) )⁶
Answer:
(cos⁡($\frac{5π}{6}$) + i sin⁡($\frac{5π}{6}$))⁶= cos($\frac{30π}{6}$) + i sin($\frac{30π}{6}$)
= cos(5π) + isin(5π)
= – 1

d. [$\frac{1}{3}$(cos⁡($\frac{3π}{2}$) + i sin⁡($\frac{3π}{2}$) )]⁴
Answer:
[$\frac{1}{3}$(cos⁡($\frac{3π}{2}$) + i sin⁡($\frac{3π}{2}$) )]⁴= ($\frac{1}{3}$)⁴ (cos(4∙$\frac{3π}{2}$) + isin(4∙$\frac{3π}{2}$))
= $\frac{1}{81}$ (cos(6π) + isin(6π))
= $\frac{1}{81}$

e. [4(cos⁡($\frac{4π}{3}$) + i sin⁡($\frac{4π}{3}$) )]^{– 4}
Answer:
[4(cos⁡($\frac{4π}{3}$) + i sin⁡($\frac{4π}{3}$) )]^{– 4}= 4^{– 4} (cos( – 4∙$\frac{4π}{3}$) + isin(4∙$\frac{4π}{3}$))
= $\frac{1}{256}$(cos( – $\frac{16π}{3}$) + isin( – $\frac{16π}{3}$))
= $\frac{1}{256}$( – $\frac{1}{2}$ + $\frac{\sqrt{3}}{2}$i)
= – $\frac{1}{512}$ + $\frac{\sqrt{3}}{512}$i

Eureka Math Precalculus Module 1 Lesson 18 Exit Ticket Answer Key

Question 1.
Write (2 + 2i)⁸ as a complex number in the form a + bi where a and b are real numbers.
Answer:
We have |2 + 2i|= 2$\sqrt{2}$ and arg⁡(2 + 2i)= $\frac{π}{4}$.
Thus, (2 + 2i)⁸= (2$\sqrt{2}$)⁸ (cos⁡(8∙$\frac{π}{4}$) + i sin⁡(8∙$\frac{π}{4}$) )= 2¹²(cos⁡(2π) + i sin⁡(2π) )= 2¹²(1 + 0i)= 2¹² + 0i.

Question 2.
Explain why a complex number of the form (a + ai)ⁿ where a is a positive real number will either be a pure imaginary or a real number when n is an even number.
Answer:
Since the argument will always be $\frac{π}{4}$, any even number multiplied by this number will be a multiple of $\frac{π}{2}$. This will result in a rotation to one of the axes, which means the complex number will either be a real number or a pure imaginary number.

Engage NY Eureka Math Precalculus Module 1 Lesson 18 Answer Key

Eureka Math Precalculus Module 1 Lesson 18 Exercise Answer Key

Eureka Math Precalculus Module 1 Lesson 18 Problem Set Answer Key

Eureka Math Precalculus Module 1 Lesson 18 Exit Ticket Answer Key

Leave a Comment Cancel Reply