Eureka Math Precalculus Module 1 Lesson 15 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 15 Answer Key

Eureka Math Precalculus Module 1 Lesson 15 Exercise Answer Key

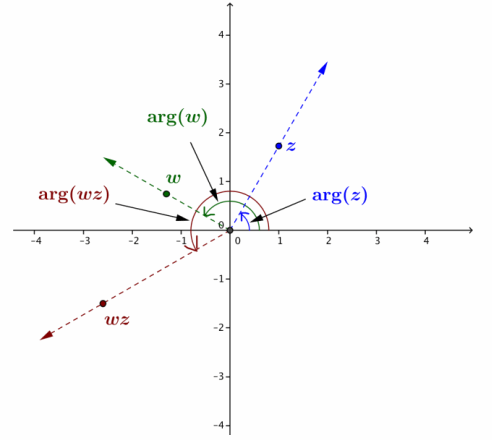
In the Opening Exercise, students review complex multiplication and consider it geometrically to justify the geometric effect of a linear transformation L(z)=(a+bi)z discovered in Lesson 13.

Opening Exercise
For each exercise below, compute the product wz. Then, plot the complex numbers z, w, and wz on the axes provided.

a. z=3+i, w=1+2i
Answer:

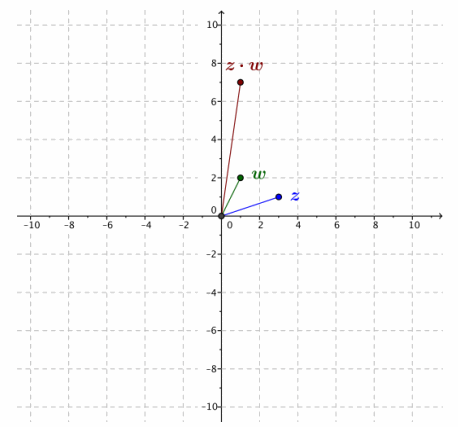
wz=(3+i)(1+2i)
=3+6i+i+2i²
=3-2+7i
=1+7i

b. z=1+2i, w=-1+4i
Answer:

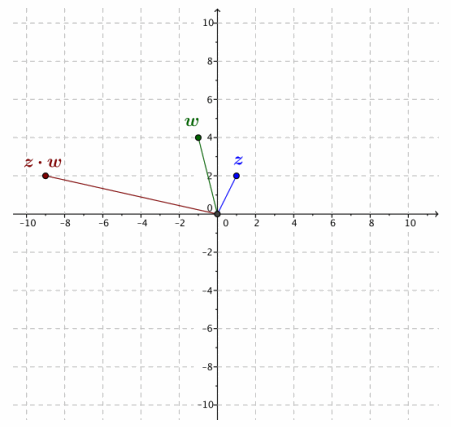
wz=(1+2i)(-1+4i)
=-1+4i-2i+8i²
=-1-8+2i
=-9+2i

c. z=-1+i, w=-2-i
Answer:

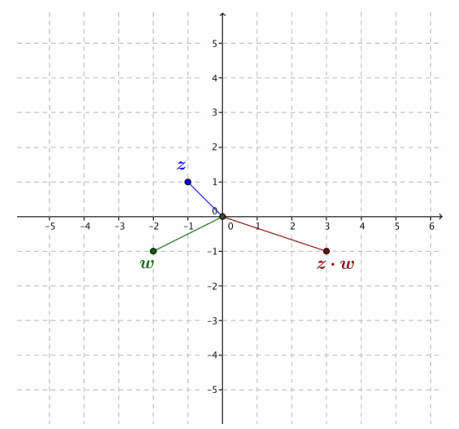
wz=(-1+i)(-2-i)
=2-2i+i-i²
=2+1-i
=3-i

d. For each part (a), (b), and (c), draw line segments connecting each point z, w, and wz to the origin. Determine a relationship between the arguments of the complex numbers z, w, and wz.
Answer:
It appears that the argument of wz is the sum of the arguments of z and w.

Exercises

Exercise 1.
Let w=a+bi and z=c+di.

a. Calculate the product wz.
Answer:
wz=(a+bi)(c+di)
=(ac-bd)+(ad+bc)i

b. Calculate the moduli |w|, |z|, and |wz|.
Answer:
|w|=\(\sqrt{a^{2}+b^{2}}\)
|z|=\(\sqrt{c^{2}+d^{2}}\)
|wz|=\(\sqrt{(a c-b d)^{2}+(a d+b c)^{2}}\)
=\(\sqrt{a^{2} c^{2}-2 a b c d+b^{2} d^{2}+a^{2} d^{2}+2 a b c d+b^{2} c^{2}}\)
=\(\sqrt{a^{2}\left(c^{2}+d^{2}\right)+b^{2}\left(c^{2}+d^{2}\right)}\)
=\(\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}\)

c. What can you conclude about the quantities |w|, |z|, and |wz|?
Answer:
From part (b), we can see that |wz|=|w| ∙ |z|.

Exercise 2.
What does the result of Exercise 1 tell us about the geometric effect of the transformation L(z)=wz?
Answer:
We see that |L(z)|=|wz|=|w| ∙ |z|, so the transformation L dilates by a factor of |w|.

Exercise 3.
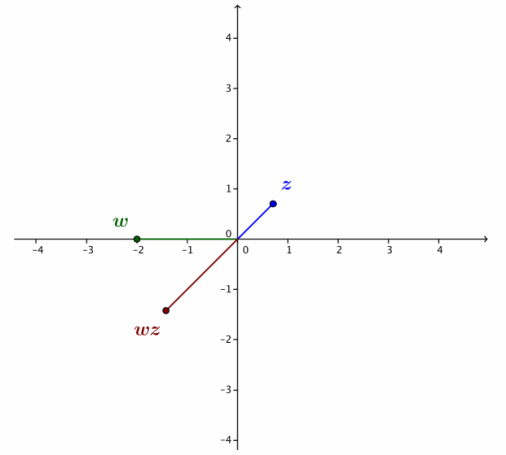
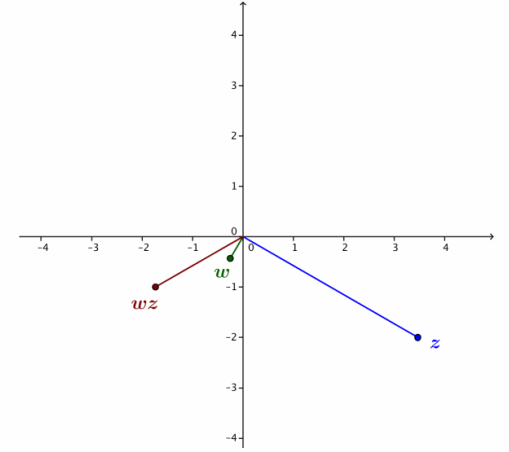
If z and w are the complex numbers with the specified arguments and moduli, locate the point that represents the product wz on the provided coordinate axes.
a. |w|=3, arg(w)=\(\frac{π}{4}\)
|z|=\(\frac{2}{3}\), arg(z)=-\(\frac{π}{2}\)

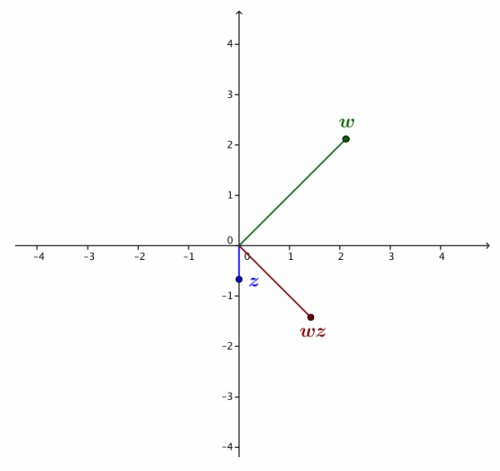
b. |w|=2, arg(w)=π
|z|=1, arg(z)=\(\frac{π}{4}\)

c. |w|=\(\frac{1}{2}\), arg(w)=\(\frac{4π}{3}\)
|z|=4, arg(z)=-\(\frac{π}{6}\)

Eureka Math Precalculus Module 1 Lesson 15 Problem Set Answer Key

Problems 1 and 2 establish that any linear transformation of the form L(z)=wz has the geometric effect of a rotation by arg⁡(w) and dilation by |w|. Problems 3 and 4 lead to the development in the next lesson in which students build new transformations from ones they already know.

Question 1.
In the lesson, we justified our observation that the geometric effect of a transformation L(z)=wz is a rotation by arg(w) and a dilation by |w| for a complex number w that is represented by a point in the first quadrant of the coordinate plane. In this exercise, we will verify that this observation is valid for any complex number w. For a complex number w=a+bi, we only considered the case where a>0 and b>0. There are eight additional possibilities we need to consider.

a. Case 1: The point representing w is the origin. That is, a=0 and b=0.
In this case, explain why L(z)=(a+bi)z has the geometric effect of rotation by arg(a+bi) and dilation by |a+bi|.
Answer:
If a+bi=0+0i=0, then arg(a+bi)=0, and |a+bi|=0. Rotating a point z by 0° does not change the location of z, and dilation by 0 sends each point to the origin. Since L(z)=0z=0 for every complex number z, we can say that L dilates by 0 and rotates by 0, so L rotates counterclockwise by arg(a+bi) and dilates by |a+bi|.

b. Case 2: The point representing w lies on the positive real axis. That is, a>0 and b=0.
In this case, explain why L(z)=(a+bi)z has the geometric effect of rotation by arg(a+bi) and dilation by |a+bi|.
Answer:
If b=0, then L(z)=az, which dilates z by a factor of a and does not rotate z. Since a+bi lies on the positive real axis, arg(a+bi)=0. Also, |a+bi|=|a|=a, since a>0. Thus, L dilates by |a+bi| and rotates counterclockwise by arg(a+bi).

c. Case 3: The point representing w lies on the negative real axis. That is, a<0 and b=0. In this case, explain why L(z)=(a+bi)z has the geometric effect of rotation by arg(a+bi) and dilation by |a+bi|. Answer: If b=0, then L(z)=az, which dilates z by a factor of |a| and rotates z by 180°. Since a+bi lies on the negative real axis, arg(a+bi)=180°. Also, |a+bi|=|a|. Thus, L dilates by |a+bi| and rotates counterclockwise by arg(a+bi). d. Case 4: The point representing w lies on the positive imaginary axis. That is, a=0 and b>0.
In this case, explain why L(z)=(a+bi)z has the geometric effect of rotation by arg(a+bi) and dilation by |a+bi|.
Answer:
If a=0, then L(z)=(bi)z, which dilates z by a factor of b and rotates z by 90° counterclockwise. Since a+bi lies on the positive imaginary axis, arg(a+bi)=90°. Also, |a+bi|=b. Thus, L dilates by |a+bi| and rotates counterclockwise by arg(a+bi).

e. Case 5: The point representing w lies on the negative imaginary axis. That is, a=0 and b<0.
In this case, explain why L(z)=(a+bi)z has the geometric effect of rotation by arg(a+bi) and dilation by |a+bi|.
Answer:
If a=0, then L(z)=(bi)z, which dilates z by a factor of |b| and rotates z by 270° counterclockwise. Since a+bi lies on the negative imaginary axis, arg(a+bi)=270°. Also, |a+bi|=|b|. Thus, L dilates by |a+bi| and rotates counterclockwise by arg(a+bi).

f. Case 6: The point representing w=a+bi lies in the second quadrant. That is, a<0 and b>0. Points representing w, z, az, (bi)z, and wz=az+(bi)z are shown in the figure below.

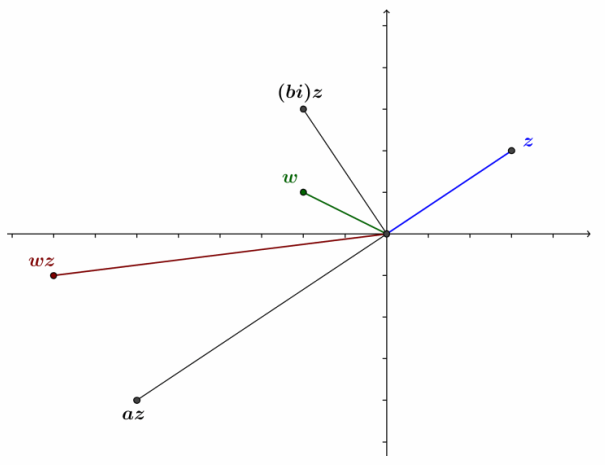
For convenience, rename the origin O, and let P=w, Q=a, R=wz, S=az, and T=z, as shown below. Let m∠POQ=θ.

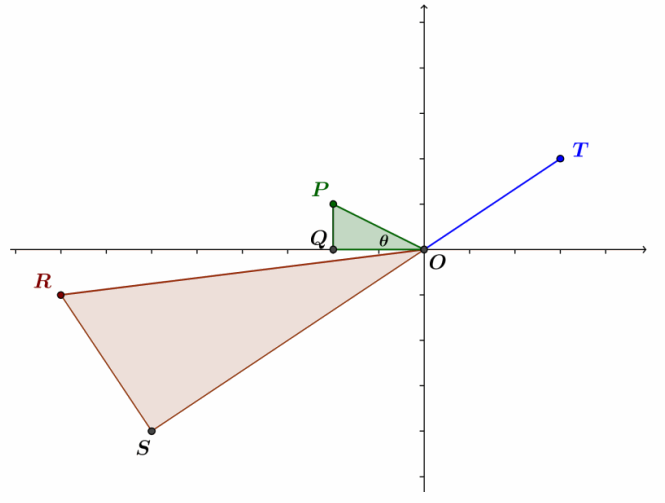
i. Argue that △OPQ ∼ △ORS.
Answer:
The lengths of the sides of the triangles are the following:
OP=|w| OR=|w| ∙ |z|
OQ=|a| OS=|a| ∙ |z|
PQ=b RS=b ∙ |z|
Thus, \(\frac{OR}{OP}\)=\(\frac{OS}{OQ}\)=\(\frac{RS}{PQ}\)=|z|, so △OPQ∼ △ORS.

ii. Express the argument of az in terms of arg(z).
Answer:
arg(az)=180°+arg(z)

iii. Express arg(w) in terms of θ, where θ=m∠POQ.
Answer:
arg(w)= 180°-θ

iv. Explain why arg(wz)=arg(az)-θ.
Answer:
Because △OPQ∼ △ORS, m∠ROS= m∠POQ=θ.
arg(wz)=arg(az)-m∠ROW
=arg(az)-m∠POQ
=arg(az)-θ

v. Combine your responses from parts (ii), (iii), and (iv) to express arg(wz) in terms of arg(z) and arg(w).
Answer:
arg(wz)=arg(az)-θ
=(180°+arg(z))-(180°-arg(w))
=arg(z)+arg(w)

g. Case 7: The point representing w=a+bi lies in the third quadrant. That is, a<0 and b<0. Points representing w, z, az, (bi)z, and wz=az+(bi)z are shown in the figure below.

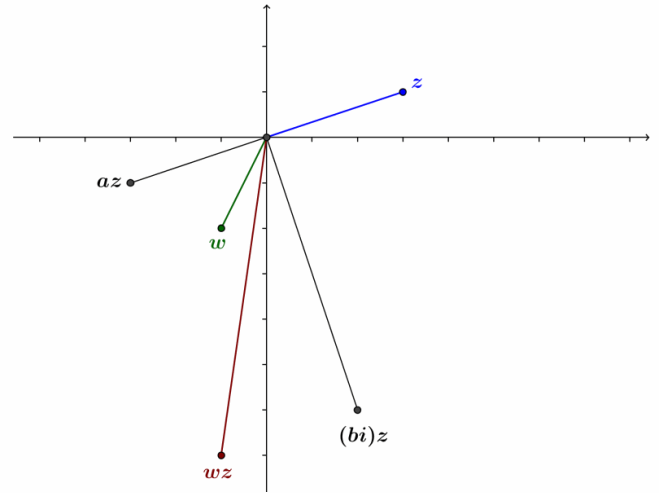
For convenience, rename the origin O, and let P=w, Q=a, R=wz, S=az, and T=z, as shown below. Let m∠POQ=θ. Answer:

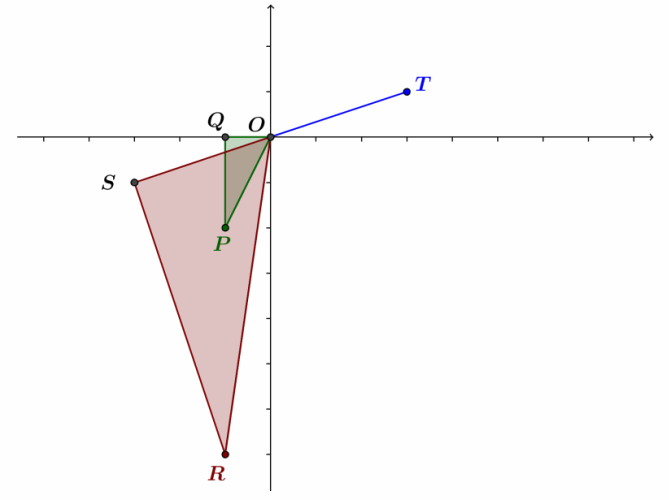
i. Argue that △OPQ∼ △ORS.
Answer:
The lengths of the sides of the triangles are as follows:
OP=|w| OR=|w| ∙ |z| OQ=|a| OS=|a| ∙ |z| PQ=|b| RS=|b| ∙ |z|
Thus, \(\frac{OR}{OP}\)=\(\frac{OS}{OQ}\)=\(\frac{RS}{PQ}\)=|z|, so △OPQ∼ △ORS.

ii. Express the argument of az in terms of arg(z).
Answer:
arg(az)=180°+arg(z)

iii. Express arg(w) in terms of θ, where θ=m∠POQ.
Answer:
arg(w)=180°+θ

iv. Explain why arg(wz)=arg(az)+θ.
Answer:
Because △OPQ∼ △ORS, m∠ROS= m∠POQ=θ.
arg(wz)=arg(az)+ m∠ROS
=arg(az)+ m∠POQ
=arg(az)+ θ

v. Combine your responses from parts (ii), (iii), and (iv) to express arg(wz) in terms of arg(z) and arg(w).
Answer:
arg(wz)=arg(az)+θ
=(180°+arg(z))+(arg(w)-180°)
=arg(z)+ arg(w)

h. Case 8: The point representing w=a+bi lies in the fourth quadrant. That is, a>0 and b<0.
Points representing w, z, az, (bi)z, and wz=az+(bi)z are shown in the figure below.
Answer:

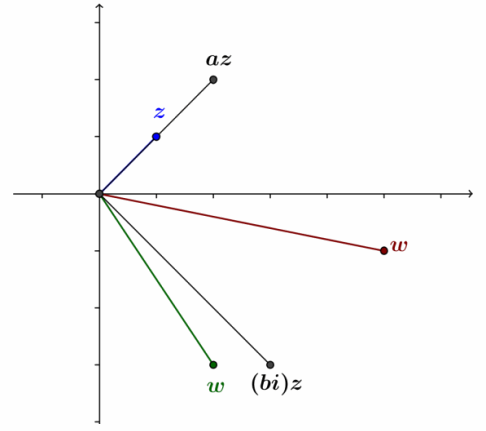
For convenience, rename the origin O, and let P=w, Q=a, R=wz, S=az, and T=z, as shown below. Let m∠POQ=θ.

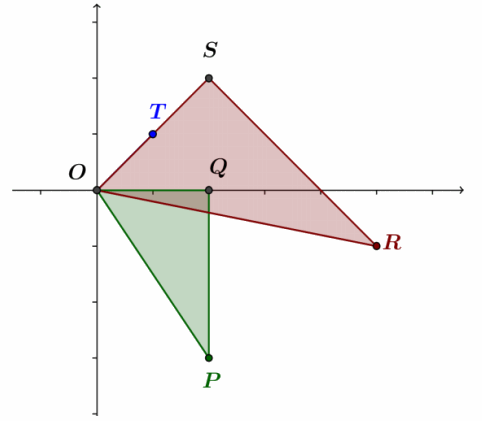
i. Argue that △OPQ ∼ △ORS.
Answer:
The lengths of the sides of the triangles are the following:
OP=|w| OR=|w| ∙ |z|
OQ=a OS=a ∙ |z|
PQ=|b| RS=|b| ∙ |z|
Thus, \(\frac{OR}{OP}\)=\(\frac{OS}{OQ}\)=\(\frac{RS}{PQ}\)=|z|, so △OPQ ∼ △ORS.

ii. Express arg(w) in terms of θ, where θ=m∠POQ.
Answer:
arg(w)= 360°-θ

iii. Explain why m∠QOR=θ-arg(z).
Answer:
Because △OPQ ∼ △ORS, m∠SOR= m∠POQ=θ.
m∠QOR=m∠SOR-m∠SOQ
=θ-m∠SOQ
=θ-arg(z)

iv. Express arg(wz) in terms of m∠QOR.
Answer:
Because △OPQ∼ △ORS, m∠ROS= m∠POQ=θ.
arg(wz)=arg(az)+ m∠ROS
=arg(az)+ m∠POQ
=arg(az)+ θ

v. Combine your responses from parts (ii), (iii), and (iv) to express arg(wz) in terms of arg(z) and arg(w).
Answer:
arg(wz)=360°-m∠QOR
=360°-(θ-arg(z))
=(360°-θ)+arg(z)
=arg(w)+ arg(z)

Question 2.
Summarize the results of Problem 1, parts (a)–(h), and the lesson.
Answer:
For any complex number w, the transformation L(z)=wz has the geometric effect of rotation by arg(w) and dilation by |w|.

Question 3.
Find a linear transformation L that will have the geometric effect of rotation by the specified amount without dilating.
a. 45° counterclockwise
Answer:
We need to find a complex number w so that |w|=1 and arg(w)=45°. Then, w can be represented by a point on the unit circle such that the ray through the origin and w is the terminal ray of the positive x-axis rotated by 45°. Then, the x-coordinate of w is cos(45°), and the y-coordinate of w is sin(45°), so we have w=cos(45°)+i sin(45°)=\(\frac{\sqrt{2}}{2}\)+\(\frac{i \sqrt{2}}{2}\). Then, L(z)= (\(\frac{\sqrt{2}}{2}\)+\(\frac{i \sqrt{2}}{2}\))z =\(\frac{\sqrt{2}}{2}\)(1+i)z.

b. 60° counterclockwise
Answer:
L(z)=(cos(60°)+i sin(60°))z
=(\(\frac{1}{2}\)+\(\frac{i \sqrt{3}}{2}\))z

c. 180° counterclockwise
Answer:
L(z)=(cos(180°)+i sin(180°))z
=-z

d. 120° counterclockwise
Answer:
L(z)=(cos(120°)+i sin(120°))z
=(-\(\frac{1}{2}\)+\(\frac{i \sqrt{3}}{2}\))z

e. 30° clockwise
Answer:
L(z)=(cos(-30°)+i sin(-30°))z
=(√\(\frac{3}{2}\)–\(\frac{1}{2}\) i)z

f. 90° clockwise
Answer:
L(z)=(cos(-90°)+i sin(-90°))z
=-iz

g. 180° clockwise
Answer:
L(z)=(cos(-180°)+i sin(-180°))z
=-z

h. 135° clockwise
Answer:
L(z)=(cos(-135°)+i sin(-135°))z
=(-\(\frac{\sqrt{2}}{2}\)–\(\frac{i \sqrt{2}}{2}\))z
=-\(\frac{\sqrt{2}}{2}\) (1+i)z

Question 4.
Suppose that we have linear transformations L₁ and L₂ as specified below. Find a formula for L₂ (L₁ (z)) for complex numbers z.

a. L₁ (z)=(1+i)z and L₂ (z)=(1-i)z
Answer:
L₂ (L₁ (z))=L₂ ((1+i)z)
=(1-i)((1+i)z)
=(1-i)(1+i)z
=2z

b. L₁ (z)=(3-2i)z and L₂ (z)=(2+3i)z
Answer:
L₂ (L₁ (z))=L₂ ((3-2i)z)
=(2+3i)((3-2i)z)
=(2+3i)(3-2i)z
=(12+5i)z

c. L₁ (z)=(-4+3i)z and L₂ (z)=(-3-i)z
Answer:
L₂ (L₁ (z))=L₂ ((-4+3i)z)
=(-3-i)((-4+3i)z)
=(-3-i)(-4+3i)z
=(15-5i)z

d. L₁ (z)=(a+bi)z and L₂ (z)=(c+di)z for real numbers a, b, c, and d.
Answer:
L₂ (L₁ (z)) =L₂((a+bi)z)
=(c+di)((a+bi)z)
=(a+bi)(c+di)z

Eureka Math Precalculus Module 1 Lesson 15 Exit Ticket Answer Key

Question 1.
What is the geometric effect of the transformation L(z)=(-6+8i)z?
Answer:
For this transformation, w=-6+8i, so |w|=\(\sqrt{(-6)^{2}+8^{2}}\)=\(\sqrt{100}\)=10. The transformation L dilates by a factor of 10 and rotates counterclockwise by arg(-6+8i).

Question 2.
Suppose that w is a complex number with |w|=\(\frac{3}{2}\) and arg⁡(w)=\(\frac{5π}{6}\), and z is a complex number with |z|=2 and arg⁡(z)=\(\frac{π}{3}\).

a. Explain how you can geometrically locate the point that represents the product wz in the coordinate plane.
Answer:
The product wz has argument \(\frac{5π}{6}\)+\(\frac{π}{3}\)=\(\frac{7π}{6}\) and modulus \(\frac{3}{2}\) ∙ 2 = 3. So, we find the point that is distance
3 units from the origin on the ray that has been rotated \(\frac{7π}{6}\) radians from the positive x-axis.

b. Plot w, z, and wz on the coordinate grid.

Answer: