Eureka Math Precalculus Module 1 Lesson 10 Answer Key

Engage NY Eureka Math Precalculus Module 1 Lesson 10 Answer Key

Eureka Math Precalculus Module 1 Lesson 10 Example Answer Key

Example 1.
Plot the given points, and then plot the image L(z)=2z.

a. z₁=3
Answer:
2z₁=6

b. z₂=2i
Answer:
2z₂=4i

c. z₃=1+i
Answer:
2z₃=2+2i

d. z₄=-4+3i
Answer:
2z₄=-8+6i

e. z₅=2-5i
Answer:
2z₅=4-10i

→ Algebraically, how did L(z)=2z affect z?
→ The coefficients doubled.
→ Geometrically, how did L(z)=2z affect z?
→ There was a dilation with scale factor 2.
→ Draw a segment from the origin to one point and its image. Confirm your conjecture by finding the length of the segments.

Assign different groups different pairs of points so as a class, all pairs are checked. Students confirm that every segment from the origin to the image is double the length of the segment from the origin to the original point.

→ Do you think the same would be true if we multiplied by a constant other than 2? Confirm your answer.
→ This is true for any constant.

Assign different groups different points by which to multiply different constants, and then have groups report their findings. This would be a good activity to use for differentiating instruction.

Example 2.
Describe the geometric effect of L(z)=(1+i)z given the following. Plot the images on graph paper, and describe the geometric effect in words.

a. z₁ =1
Answer:
L(z₁)=(1+i)(1)=1+i, no change

b. z₂=i
Answer:
L(z₂)=(1+i)i=i-1=-1+i, a 90° counterclockwise rotation about the origin

c. z₃=1+i
Answer:
L(z₃)=(1+i)(1+i)=1+2i-1=2i, a 45° counterclockwise rotation about the origin and a dilation with a scale factor of \(\sqrt{2}\)

d. z₄=4+6i
Answer:
L(z₄)=(1+i)(4+6i)=4+10i-6=-2+10i, a clockwise rotation about the origin of some angle measure θ and a dilation with a scale factor greater than 1

→ What was the geometric result of multiplying the complex number by 1?
→ There was no change.
→ Are you surprised by this result?
→No, multiplying by 1 always results in the number you started with. It is the multiplicative identity.
→ What was the geometric result of multiplying by i?
→ The result was a 90° counterclockwise rotation about the origin. The point was reflected across the imaginary axis.
→ Did this result surprise you?
→ No, multiplying by i always results in a 90° counterclockwise rotation about the origin, but it is not always a reflection across the imaginary axis.
→ What would always create a reflection across the real axis?
→ Taking the complex conjugate, 1-i
→ What would create a reflection across the imaginary axis?
→ The opposite of the complex conjugate, -1+i
→ What was the geometric result of multiplying by 1+i?
→ There was a clockwise rotation and a dilation.
→ Can you guess how many degrees the point rotated? Explain.

It is ok if students do not yet fully grasp the degree of rotation; they study this in great detail in future lessons.

→ 45°. The angle of the segment joining the origin to the original point is 45° because if you draw a right triangle, each leg is 1 unit, so the triangle is a special 45°–45°–90° triangle. The image is on the y-axis, so that is a 90°. If the original point was at a 45° angle and the reflection is at an angle of 90°, the angle that the point rotated was 45°.

→ What was the scale factor of the dilation? Explain.

→ The segment joining the origin and the original point was the hypotenuse of a 45°–45°–90° with legs of length 1 unit, so it was \(\sqrt{2}\) units in length by the Pythagorean theorem. The segment joining the origin and the image is 2 units in length. This means that the original length was multiplied by a scale factor of \(\sqrt{2}\) to get the length of the segment containing the image.

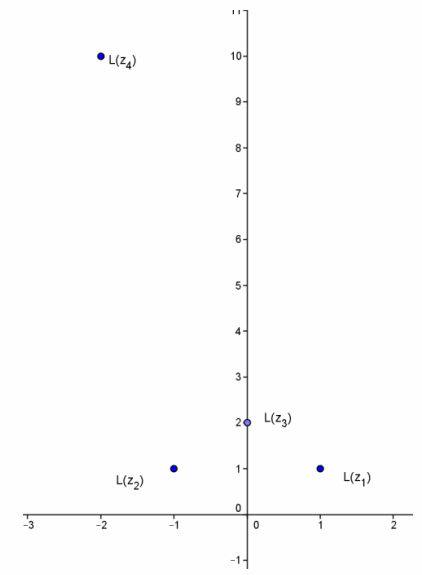
→ What was the result of multiplying by 4+6i?
→ A clockwise rotation and a dilation greater than 1
→ Can you determine the angle of rotation and the dilation scale factor?
Students are probably not able to determine the answers for this result, but this is studied in detail later. It can be left for them to think about.
→ The scale factor is \(\sqrt{2}\)6, and θ= π – tan^-1(5)=1.768 radians=101.31°.

Eureka Math Precalculus Module 1 Lesson 10 Exercise Answer Key

Opening Exercises

Question 1.
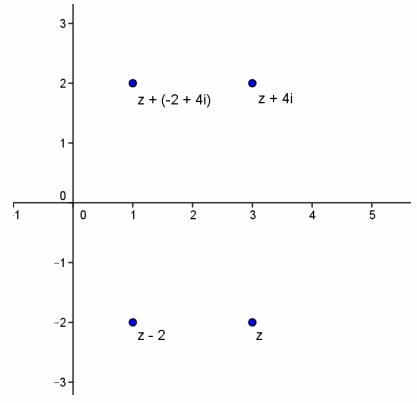
Given z=3-2i, plot and label the following, and describe the geometric effect of the operation.

a. z
Answer:
3 units on the real axis to the right of the origin and 2 units on the imaginary axis below the origin

b. z-2
Answer:
2 units on the real axis to the left of z

c. z+4i
Answer:
4 units on the imaginary axis above z

d. z+(-2+4i)
Answer:
2 units on the real axis to the left of z and 4 units on the imaginary axis above z

Question 2.
Describe the geometric effect of the following:
a. Multiplying by i
Answer:
A 90° rotation about the origin

b. Taking the complex conjugate
Answer:
Reflects the imaginary number across the real axis

c. What operation reflects a complex number across the imaginary axis?
Answer:
The opposite of the conjugate (-\(\overline{\boldsymbol{z}}\)) reflects a complex number across the imaginary axis.

Exercises
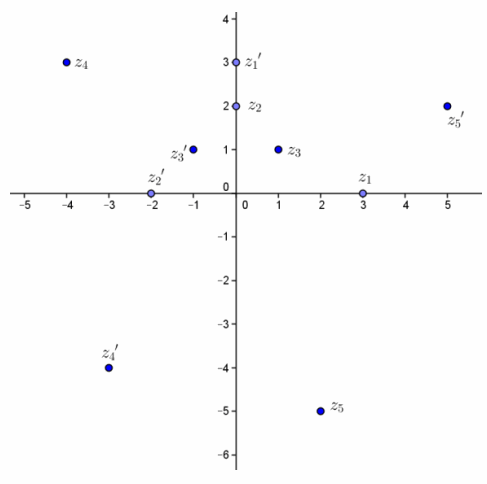
Plot the given points, and then plot the image L(z)=iz.

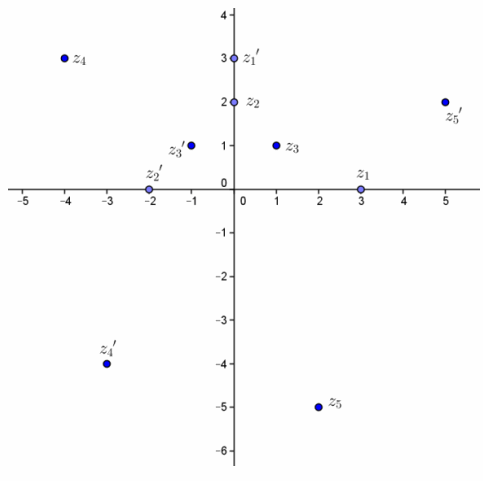
Question 1.
z₁=3
Answer:
iz₁=3i

Question 2.
z₂=2i
Answer:
iz₂=-2

Question 3.
z₃=1+i
Answer:
iz₃=i(1+i)=i-1=-1+i

Question 4.
z₄=-4+3i
Answer:
iz₄=i(-4+3i)=-4i-3=-3-4i

Question 5.
z₅=2–5i
Answer:
iz₅=i(2-5i)=2i+5=5+2i

Question 6.
What is the geometric effect of the transformation? Confirm your conjecture using the slope of the segment joining the origin to the point and then to its image.
Answer:
Multiplying by i rotates the point 90° counterclockwise about the origin. This is confirmed because the slopes of the segments joining the origin and the original points and the slopes of the segments joining the origin and the image of those points are opposite reciprocals, which means the segments are perpendicular.

Question 7.
Is L(z) a linear transformation? Explain how you know.
Answer:
Yes, L(z+w)=L(z)+L(w) and kL(z)=L(kz).

Eureka Math Precalculus Module 1 Lesson 10 Problem Set Answer Key

Question 1.
Let z=-4+2i. Simplify the following, and describe the geometric effect of the operation. Plot the result in the complex plane.

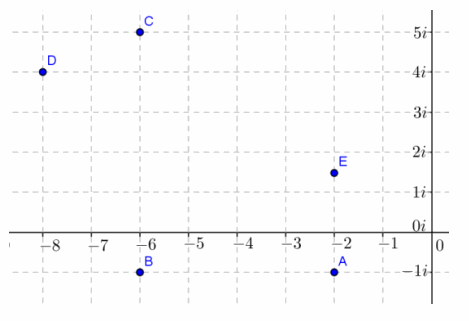
a. z+2-3i
Answer:
-4+2i+2-3i=-2-i
z is shifted 2 units to the right and 3 units downward.

b. z-2-3i
Answer:
-4+2i-2-3i=-6-i
z is shifted 2 units to the left and 3 units downward.

c. z-(2-3i)
Answer:
-4+2i-(2-3i)=-4+2i-2+3i=-6+5i
z is shifted 2 units to the left and 3 units upward.

d. 2z
Answer:
2(-4+2i)=-8+4i
z has a dilation with a scale factor of 2.

e. \(\frac{2}{2}\)
Answer:
\(\frac{-4+2 i}{2}\) = -2 + \(\frac{3}{2}\)
\(\frac{-4+2i}{2}\)=-2+\(\frac{3}{2}\)i
z has a dilation with a scale factor of \(\frac{1}{2}\).

Question 2.
Let z=1+2i. Simplify the following, and describe the geometric effect of the operation.

a. iz
Answer:
iz=-2+i
z is rotated 90° counterclockwise.

b. i²z
Answer:
i²z=(-1)(1+2i)=-1-2i
OR
i²z=i∙i∙(1+2i)=i(i-2)=-1-2i
z is rotated 180° counterclockwise.

c. \(\overline{\boldsymbol{z}}\)
Answer:
\(\overline{\boldsymbol{z}}\)=1-2i
z is reflected about the real axis.

d. –\(\overline{\boldsymbol{z}}\)
Answer:
–\(\overline{\boldsymbol{z}}\)=-(1-2i)=-1+2i
z is reflected about the imaginary axis.

e. i\(\overline{\boldsymbol{z}}\)
Answer:
i\(\overline{\boldsymbol{z}}\)=i(1-2i)=2+i
z is reflected about the real axis first and then is rotated 90° counterclockwise.

f. 2iz
Answer:
2iz=2i(1+2i)=-4+2i
z is rotated 90° counterclockwise and then has a dilation with a scale factor of 2.

g. iz+5-3i
Answer:
iz+5-3i=i(1+2i)+5-3i=-2+i+5-3i=3-2i
z is rotated 90° counterclockwise first and then shifted 5 units to the right and 3 units downward.

Question 3.
Simplify the following expressions.
a. (4-2i)(5-3i)
Answer:
14-22i

b. (-2+3i)(-2-3i)
Answer:
13

c. (1+i)²
Answer:
2i

d. (1+i)¹⁰ (Hint: b^nm=(bⁿ)^m)
Answer:
(1+i)¹⁰=((1+i)²)⁵=(2i)⁵=32i

e. \(\frac{-1+2 i}{1-2 i}\)
Answer:

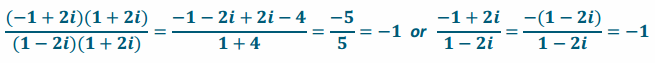
f. \(\frac{x^{2}+4}{x-2 i}\), \frac{x^{2}+4}{x-2 i}
Answer:
\(\frac{x^{2}+4}{x-2 i}\) = \(\frac{(x+2 i)(x-2 i)}{x-2 i}\) = x + 2i

Question 4.
Given z=2+i, describe the geometric effect of the following. Plot the result.

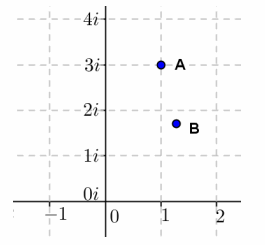
a. z(1+i)
z is rotated 45° counterclockwise and has a scale factor \(\sqrt{2}\) multiplying to |z|.

b. z(\(\frac{\sqrt{3}}{2}\)+\(\frac{1}{2}\)i)
Answer:
z is rotated 30° counterclockwise and has a scale factor 1 multiplying to |z|.

Question 5.
We learned that multiplying by i produces a 90° counterclockwise rotation about the origin. What do we need to multiply by to produce a 90° clockwise rotation about the origin?
Answer:
We need to multiply by \(\frac{1}{i}\). If w=iz (w is a 90° counterclockwise rotation about the origin from z), z=\(\frac{w}{i}\), which means that if we divide w by i, we will get to z, which will create a 90° clockwise rotation about the origin from w. Another response: 90° clockwise is 270° counterclockwise, so you could multiply by i³ to map (a,b) to (b,-a).

Question 6.
Given z is a complex number a+bi, determine if L(z) is a linear transformation. Explain why or why not.

a. L(z)=i³ z
Answer:
Yes. L(z)=-iz, so L(z+w)=-iz+-iw and L(z)+L(w)=-iz+-iw.
kL(z)=k(-iz) and L(kz)=-i(kz).
Since L(z+w)=L(z)+L(w) and kL(z)=L(kz), the function is a linear transformation.

b. L(z)=z+4i
Answer:
No. L(z+w)=z+w+4i and L(z)+L(w)=z+4i+w+4i. kL(z)=k(z+4i) and L(kz)=kz+4i.
Since L(z+w)=L(z)+L(w) and kL(z)≠L(kz), the function is not a linear transformation.

Eureka Math Precalculus Module 1 Lesson 10 Exit Ticket Answer Key

Question 1.
Given T(z)=z, describe the geometric effect of the following:

a. T(z)=5z
Answer:
It has a dilation with a scale factor of 5.

b. T(z)=\(\frac{z}{2}\)
Answer:
It has a dilation with a scale factor of \(\frac{1}{2}\).

c. T(z)=iz
Answer:
It has a 90° counterclockwise rotation about the origin.

Question 2.
If z=-2+3i is the result of a 90° counterclockwise rotation about the origin from w, find w. Plot z and w in the complex plane.
Answer:

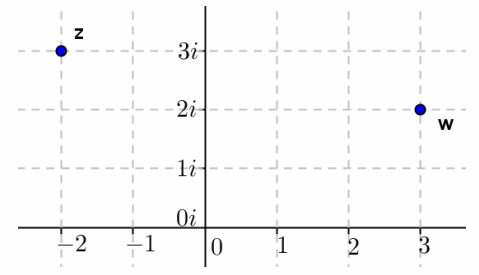
z=i∙w
-2+3i=i∙w
w=\(\frac{-2+3 i}{i}\)
w=\(\frac{(-2+3 i) \cdot i}{i \cdot i}\)
w=\(\frac{-3-2 i}{-1}\)
w=3+2i

Question 3.
Explain the geometric effect of z if you multiply z by w, where w=1+i.
Answer:
It has a 45° counterclockwise rotation about the origin and a dilation with a scale factor of \(\sqrt{2}\).