Eureka Math Grade 8 Module 7 Lesson 5 Answer Key

Engage NY Eureka Math 8th Grade Module 7 Lesson 5 Answer Key

Eureka Math Grade 8 Module 7 Lesson 5 Example Answer Key

Example 1.
x³ + 9x = \(\frac{1}{2}\) (18x + 54)
Answer:
Now that we know about square roots and cube roots, we can combine that knowledge with our knowledge of the properties of equality to begin solving nonlinear equations like x³ + 9x = \(\frac{1}{2}\) (18x + 54). Transform the equation until you can determine the positive value of x that makes the equation true.
Challenge students to solve the equation independently or in pairs. Have students share their strategy for solving the equation. Ask them to explain each step.
x³ + 9x = \(\frac{1}{2}\) (18x + 54)
x³ + 9x = 9x + 27
x³ + 9x – 9x = 9x – 9x + 27
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = \(\sqrt[3]{3^{3}}\)
x = 3
Now, we verify our solution is correct.
3³ + 9(3) = \(\frac{1}{2}\) (18(3) + 54)
27 + 27 = \(\frac{1}{2}\) (54 + 54)
54 = \(\frac{1}{2}\) (108)
54 = 54
Since the left side is the same as the right side, our solution is correct.

Example 2.
x(x – 3) – 51 = – 3x + 13
Answer:
Let’s look at another nonlinear equation. Find the positive value of x that makes the equation true: x(x – 3) – 51 = – 3x + 13.
Provide students with time to solve the equation independently or in pairs. Have students share their strategy for solving the equation. Ask them to explain each step.
Sample response:
x(x – 3) – 51 = – 3x + 13
x² – 3x – 51 = – 3x + 13
x² – 3x + 3x – 51 = – 3x + 3x + 13
x² – 51 = 13
x² – 51 + 51 = 13 + 51
x² = 64
\(\sqrt{x^{2}}\) = ±\(\sqrt{64}\)
x = ±\(\sqrt{64}\)
x = ±8
Now we verify our solution is correct.
Provide students time to check their work.
Let x = 8.
8(8 – 3) – 51 = – 3(8) + 13
8(5) – 51 = – 24 + 13
40 – 51 = – 11
– 11 = – 11

Let x = – 8.
– 8( – 8 – 3) – 51 = – 3( – 8) + 13
– 8( – 11) – 51 = 24 + 13
88 – 51 = 37
37 = 37
Now it is clear that the left side is exactly the same as the right side, and our solution is correct.

Eureka Math Grade 8 Module 7 Lesson 5 Exercise Answer Key

Find the positive value of x that makes each equation true, and then verify your solution is correct.
Exercise 1.
a. Solve x² – 14 = 5x + 67 – 5x.
Answer:
x² – 14 = 5x + 67 – 5x
x² – 14 = 67
x² – 14 + 14 = 67 + 14
x² = 81
\(\sqrt{x^{2}}\) = ±\(\sqrt{81}\)
x = ±\(\sqrt{81}\)
x = ±9

Check:
9² – 14 = 5(9) + 67 – 5(9)
81 – 14 = 45 + 67 – 45
67 = 67

( – 9)² – 14 = 5( – 9) + 67 – 5( – 9)
81 – 14 = – 45 + 67 + 45
67 = 67

b. Explain how you solved the equation.
Answer:
To solve the equation, I had to first use the properties of equality to transform the equation into the form of x² = 81. Then, I had to take the square root of both sides of the equation to determine that x = 9 since the number x is being squared.

Exercise 2.
Solve and simplify: x(x – 1) = 121 – x.
Answer:
x(x – 1) = 121 – x
x² – x = 121 – x
x² – x + x = 121 – x + x
x² = 121
\(\sqrt{x^{2}}\) = ±\(\sqrt{121}\)
x = ±\(\sqrt{121}\)
x = ±11

Check:
11(11 – 1) = 121 – 11
11(10) = 110
110 = 110

– 11( – 11 – 1) = 121 – ( – 11)
– 11( – 12) = 121 + 11
132 = 132

Exercise 3.
A square has a side length of 3x inches and an area of 324 in². What is the value of x?
Answer:
(3x)² = 324
3² x² = 324
9x² = 324
\(\frac{9 x^{2}}{9}\) = \(\frac{324}{9}\)
x² = 36
\(\sqrt{x^{2}}\) = \(\sqrt{36}\)
x = 6

Check:
(3(6)) ² = 324
18² = 324
324 = 324
A negative number would not make sense as a length, so x = 6.

Exercise 4.
– 3x³ + 14 = – 67
Answer:
– 3x³ + 14 = – 67
– 3x³ + 14 – 14 = – 67 – 14
– 3x³ = – 81
\(\frac{ – 3 x^{3}}{3}\) = \(\frac{ – 81}{ – 3}\)
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = 3

Check:
– 3(3)³ + 14 = – 67
– 3(27) + 14 = – 67
– 81 + 14 = – 67
– 67 = – 67

Exercise 5.
x(x + 4) – 3 = 4(x + 19.5)
Answer:
x(x + 4) – 3 = 4(x + 19.5)
x² + 4x – 3 = 4x + 78
x² + 4x – 4x – 3 = 4x – 4x + 78
x² – 3 = 78
x² – 3 + 3 = 78 + 3
x² = 81
\(\sqrt{x^{2}}\) = ±\(\sqrt{81}\)
x = ±9

Check:
9(9 + 4) – 3 = 4(9 + 19.5)
9(13) – 3 = 4(28.5)
117 – 3 = 114
114 = 114

– 9( – 9 + 4) – 3 = 4( – 9 + 19.5)
– 9( – 5) – 3 = 4(10.5)
45 – 3 = 42
42 = 42

Exercise 6.
216 + x = x(x² – 5) + 6x
Answer:
216 + x = x(x² – 5) + 6x
216 + x = x³ – 5x + 6x
216 + x = x³ + x
216 + x – x = x³ + x – x
216 = x³
\(\sqrt [ 3 ]{ 216 }\) = \(\sqrt[3]{x^{3}}\)
6 = x

Check:
216 + 6 = 6(6² – 5) + 6(6)
222 = 6(31) + 36
222 = 186 + 36
222 = 222

Exercise 7.
a. What are we trying to determine in the diagram below?

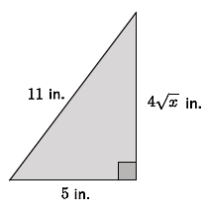
Answer:
We need to determine the value of x so that its square root, multiplied by 4, satisfies the equation
5² + (4\(\sqrt{x}\))² = 11².

b. Determine the value of x, and check your answer.
Answer:
5² + (4\(\sqrt{x}\))² = 11²
25 + 4² (\(\sqrt{x}\))² = 121
25 – 25 + 4² (\(\sqrt{x}\))² = 121 – 25
16x = 96
\(\frac{16x}{16}\) = \(\frac{96}{16}\)
x = 6
The value of x is 6.

Check:
5² + (4\(\sqrt{6}\))² = 11²
25 + 16(6) = 121
25 + 96 = 121
121 = 121

Eureka Math Grade 8 Module 7 Lesson 5 Problem Set Answer Key

Find the positive value of x that makes each equation true, and then verify your solution is correct.
Question 1.
x² (x + 7) = \(\frac{1}{2}\) (14x² + 16)
Answer:
x² (x + 7) = \(\frac{1}{2}\) (14x² + 16)
x³ + 7x² = 7x² + 8
x³ + 7x² – 7x² = 7x² – 7x² + 8
x³ = 8
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 8 }\)
x = 2

Check:
2² (2 + 7) = \(\frac{1}{2}\) (14(2² ) + 16)
4(9) = \(\frac{1}{2}\) (56 + 16)
36 = \(\frac{1}{2}\) (72)
36 = 36

Question 2.
x³ = 1331 ^{– 1}
Answer:
x³ = 1331 ^{– 1}
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{1331^{ – 1}}\)
x = \(\sqrt[3]{\frac{1}{1331}}\)
x = \(\sqrt[3]{\frac{1}{11^{3}}}\)
x = \(\frac{1}{11}\)

Check:
(\(\left(\frac{1}{11}\right)^{3}\))³ = 1331 ^{– 1}
\(\frac{1}{11^{3}}\) = 1331 ^{– 1}
\(\frac{1}{1331}\) = 1331 ^{– 1}
1331 ^{– 1} = 1331 ^{– 1}

Question 3.
Determine the positive value of x that makes the equation true, and then explain how you solved the equation.
\(\frac{x^{9}}{x^{7}}\) – 49 = 0
Answer:
\(\frac{x^{9}}{x^{7}}\) – 49 = 0
x² – 49 = 0
x² – 49 + 49 = 0 + 49
x² = 49
\(\sqrt{x^{2}}\) = \(\sqrt{49}\)
x = 7

Check:
7² – 49 = 0
49 – 49 = 0
0 = 0
To solve the equation, I first had to simplify the expression \(\frac{x^{9}}{x^{7}}\) to x². Next, I used the properties of equality to transform the equation into x² = 49. Finally, I had to take the square root of both sides of the equation to solve for x.

Question 4.
Determine the positive value of x that makes the equation true.
(8x)² = 1
Answer:
(8x)² = 1
64x² = 1
\(\sqrt{64^{2}}\) = \(\sqrt{1}\)
8x = 1
\(\frac{8x}{8}\) = \(\frac{1}{8}\)
x = \(\frac{1}{8}\)

Check:
(8(\(\frac{1}{8}\)))² = 1
1² = 1
1 = 1

Question 5.
(9\(\sqrt{x}\))² – 43x = 76
Answer:
(9\(\sqrt{x}\))² – 43x = 76
9² (√x)² – 43x = 76
81x – 43x = 76
38x = 76
\(\frac{38x}{38}\) = \(\frac{76}{38}\)
x = 2

Check:
(9(\(\sqrt{2}\)))² – 43(2) = 76
9² (\(\sqrt{2}\))² – 86 = 76
81(2) – 86 = 76
162 – 86 = 76
76 = 76

Question 6.
Determine the length of the hypotenuse of the right triangle below.

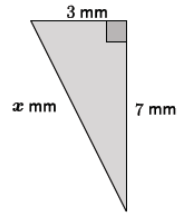
Answer:
3² + 7² = x²
9 + 49 = x²
58 = x²
\(\sqrt{58}\) = \(\sqrt{x^{2}}\)
\(\sqrt{58}\) = x

Check:
3² + 7² = (\(\sqrt{52}\))²
9 + 49 = 58
58 = 58
Since x = \(\sqrt{58}\), the length of the hypotenuse is \(\sqrt{58}\) mm.

Question 7.
Determine the length of the legs in the right triangle below.

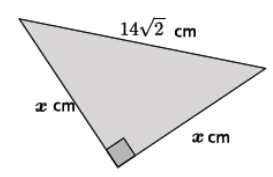
Answer:
x² + x² = (14\(\sqrt{2}\))²
2x² = 14² (\(\sqrt{2}\))²
2x² = 196(2)
\(\frac{2 x^{2}}{2}\) = \(\frac{196(2)}{2}\)
x² = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = \(\sqrt{14^{2}}\)
x = 14

Check:
14² + 14² = (14\(\sqrt{2}\))²
196 + 196 = 14² (\(\sqrt{2}\))²
392 = 196(2)
392 = 392
Since x = 14, the length of each of the legs of the right triangle is 14 cm.

Question 8.
An equilateral triangle has side lengths of 6 cm. What is the height of the triangle? What is the area of the triangle?

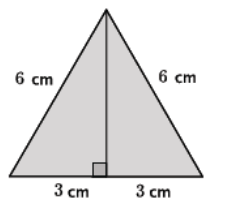
Answer:
Note: This problem has two solutions, one with a simplified root and one without. Choose the appropriate solution for your classes based on how much simplifying you have taught them.
Let h cm represent the height of the triangle.
3² + h² = 6²
9 + h² = 36
9 – 9 + h² = 36 – 9
h² = 27
\(\sqrt{h^{2}}\) = \(\sqrt{27}\)
h = \(\sqrt{27}\)
h = \(\sqrt{3^{3}}\)
h = \(\sqrt{3^{2}}\)×\(\sqrt{3}\)
h = 3\(\sqrt{3}\)

Let A represent the area of the triangle.
A = \(\frac{6(3 \sqrt{3})}{2}\))
A = 3(3\(\sqrt{3}\))
A = 9\(\sqrt{3}\)
Simplified: The height of the triangle is 3\(\sqrt{3}\) cm, and the area is 9\(\sqrt{3}\) cm².
Unsimplified: The height of the triangle is \(\sqrt{27}\) cm, and the area is 3\(\sqrt{27}\) cm²

Question 9.
Challenge: Find the positive value of x that makes the equation true.
(\(\frac{1}{2}\) x)² – 3x = 7x + 8 – 10x
Answer:
(\(\frac{1}{2}\) x)² – 3x = 7x + 8 – 10x
\(\frac{1}{4}\) x² – 3x = – 3x + 8
\(\frac{1}{4}\) x² – 3x + 3x = – 3x + 3x + 8
\(\frac{1}{4}\) x² = 8
4(\(\frac{1}{4}\)) x² = 8(4)
x² = 32
\(\sqrt{x^{2}}\) = \(\sqrt{32}\)
x = \(\sqrt{2^{5}}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2}\)
x = 4\(\sqrt{2}\)

Check:
(\(\frac{1}{2}\) (4\(\sqrt{2}\)))² – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) + 8 – 10(4\(\sqrt{2}\))
\(\frac{1}{4}\) (16)(2) – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) – 10(4\(\sqrt{2}\)) + 8
\(\frac{32}{4}\) – 3(4\(\sqrt{2}\)) = 7(4\(\sqrt{2}\)) – 10(4\(\sqrt{2}\)) + 8
8 – 3(4\(\sqrt{2}\)) = (7 – 10)(4\(\sqrt{2}\)) + 8
8 – 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\)) + 8
8 – 8 – 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\)) + 8 – 8
– 3(4\(\sqrt{2}\)) = – 3(4\(\sqrt{2}\))

Question 10.
Challenge: Find the positive value of x that makes the equation true.
11x + x(x – 4) = 7(x + 9)
Answer:
11x + x(x – 4) = 7(x + 9)
11x + x² – 4x = 7x + 63
7x + x² = 7x + 63
7x – 7x + x² = 7x – 7x + 63
x² = 63
\(\sqrt{x^{2}}\)) = \(\sqrt{63}\)
x = \(\sqrt{\left(3^{2}\right)(7)}\)
x = \(\sqrt{3^{2}}\) ⋅ \(\sqrt{7}\)
x = 3\(\sqrt{7}\)

Check:
11(3\(\sqrt{7}\)) + 3\(\sqrt{7}\) (3\(\sqrt{7}\) – 4) = 7(3\(\sqrt{7}\) + 9)
33\(\sqrt{7}\) + 3² (\(\sqrt{7}\))² – 4(3\(\sqrt{7}\)) = 21\(\sqrt{7}\) + 63
33\(\sqrt{7}\) – 4(3\(\sqrt{7}\)) + 9(7) = 21\(\sqrt{7}\) + 63
33\(\sqrt{7}\) – 12\(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
(33 – 12) \(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
21\(\sqrt{7}\) + 63 = 21\(\sqrt{7}\) + 63
21\(\sqrt{7}\) + 63 – 63 = 21\(\sqrt{7}\) + 63 – 63
21\(\sqrt{7}\) = 21\(\sqrt{7}\)

Eureka Math Grade 8 Module 7 Lesson 5 Exit Ticket Answer Key

Question 1.
Find the positive value of x that makes the equation true, and then verify your solution is correct.
x² + 4x = 4(x + 16)
Answer:
x² + 4x = 4(x + 16)
x² + 4x = 4x + 64
x² + 4x – 4x = 4x – 4x + 64
x² = 64
\(\sqrt{x^{2}}\) = \(\sqrt{64}\)
x = 8

Check:
8² + 4(8) = 4(8 + 16)
64 + 32 = 4(24)
96 = 96

Question 2.
Find the positive value of x that makes the equation true, and then verify your solution is correct.
(4x)³ = 1728
Answer:
(4x)³ = 1728
64x³ = 1728
\(\frac{1}{64}\)(64x³) = (1728)\(\frac{1}{64}\)
x³ = 27
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 27 }\)
x = 3

Check:
(4(3))³ = 1728
12³ = 1728
1728 = 1728