Engage NY Eureka Math 8th Grade Module 7 Lesson 16 Answer Key
Eureka Math Grade 8 Module 7 Lesson 16 Classwork Answer Key
Classwork
Proof of the Converse of the Pythagorean Theorem
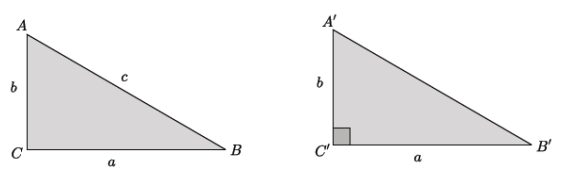
Answer:
→ What do we know or not know about each of these triangles?
In the first triangle, ABC, we know that a2 + b2 = c2. We do not know if angle C is a right angle.
In the second triangle, A’B’C’, we know that it is a right triangle.
→ What conclusions can we draw from this?
By applying the Pythagorean theorem to △A’B’C’, we get |A’B’|2 = a2 + b2. Since we are given
c2 = a2 + b2, then by substitution, |A’B’|2 = c2, and then |A’B’| = c. Since c is also |AB|, then |A’B’| = |AB|. That means that both triangles have sides a, b, and c that are the exact same lengths.
→ Recall that we would like to prove that ∠ACB is a right angle, that it maps to ∠A’ C’ B’. If we can translate
△ABC so that A goes to A’, B goes to B’, and C goes to C’, it follows that all three angles in the triangle will match. In particular, that ∠ACB maps to the right angle ∠A’ C’ B’, and so is a right angle, too.
→ We can certainly perform a translation that takes B to B’ and C to C’ because segments BC and B’C’ are the same length. Must this translation take A to A’? What goes wrong mathematically if it misses and translates to a different point A” as shown below?
In this picture, we’ve drawn A” to the left of \(\overline{A{\prime} C{\prime}}\). The reasoning that follows works just as well for a picture with A” to the right of \(\overline{A{\prime} C{\prime}}\) instead.
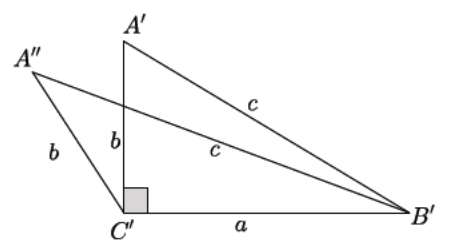
Provide time for students to think of what may go wrong mathematically. If needed, prompt them to notice the two isosceles triangles in the diagram, △A”C’A’ and △A”B’A’ and the four angles w1,w2,w3,w4 labeled as shown in the diagram below.
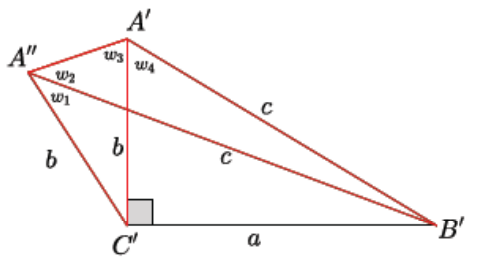
△A”C’A’ is isosceles and therefore has base angles that are equal in measure:
w1 + w2 = w3.
△A”B’A’ is isosceles and therefore has base angles that are equal in measure:
w2 = w3 + w4.
These two equations give w1 + w3 + w4 = w3, which is equal to w1 + w4 = 0, which is obviously not true.
Therefore, the translation must map A to A’, and since translations preserve the measures of angles, we can conclude that the measure of ∠ACB is equal to the measure of ∠A’C’B’, and ∠ACB is a right angle.
Finally, if a triangle has side lengths of a,b and c, with c the longest length, that don’t satisfy the equation a2 + b2 = c2, then the triangle cannot be a right triangle.
Eureka Math Grade 8 Module 7 Lesson 16 Exercise Answer Key
Exercises 1–7
Exercise 1.
Is the triangle with leg lengths of 3 mi. and 8 mi. and hypotenuse of length \(\sqrt{73}\) mi. a right triangle? Show your work, and answer in a complete sentence.
Answer:
32 + 82 = (\(\sqrt{73}\))2
9 + 64 = 73
73 = 73
Yes, the triangle with leg lengths of 3 mi. and 8 mi. and hypotenuse of length \(\sqrt{73}\) mi. is a right triangle because it satisfies the Pythagorean theorem.
Exercise 2.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.
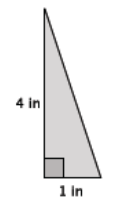
Answer:
Let c in. represent the length of the hypotenuse of the triangle.
12 + 42 = c2
1 + 16 = c2
17 = c2
\(\sqrt{17}\) = c
4.1≈c
The length of the hypotenuse of the right triangle is exactly \(\sqrt{17}\) inches and approximately 4.1 inches.
Exercise 3.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.
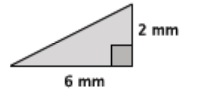
Answer:
Let c mm represent the length of the hypotenuse of the triangle.
22 + 62 = c2
4 + 36 = c2
40 = c2
\(\sqrt{40}\) = c
\(\sqrt{2^{3}}\)×\(\sqrt{5}\) = c
\(\sqrt{2^{2}}\)×\(\sqrt{2}\)×\(\sqrt{5}\) = c
2\(\sqrt{10}\) = c
The length of the hypotenuse of the right triangle is exactly 2\(\sqrt{10}\) mm and approximately 6.3 mm.
Exercise 4.
Is the triangle with leg lengths of 9 in. and 9 in. and hypotenuse of length \(\sqrt{175}\) in. a right triangle? Show your work, and answer in a complete sentence.
Answer:
92 + 92 = (\(\sqrt{175}\))2
81 + 81 = 175
162 ≠ 175
No, the triangle with leg lengths of 9 in. and 9 in. and hypotenuse of length \(\sqrt{175}\) in. is not a right triangle because the lengths do not satisfy the Pythagorean theorem.
Exercise 5.
Is the triangle with leg lengths of √(28 ) cm and 6 cm and hypotenuse of length 8 cm a right triangle? Show your work, and answer in a complete sentence.
Answer:
(\(\sqrt{28}\))2 + 62 = 82
28 + 36 = 64
64 = 64
Yes, the triangle with leg lengths of \(\sqrt{28}\) cm and 6 cm and hypotenuse of length 8 cm is a right triangle because the lengths satisfy the Pythagorean theorem.
Exercise 6.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence.
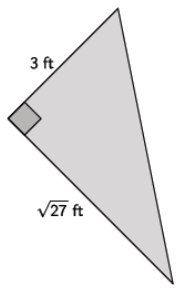
Answer:
Let c ft. represent the length of the hypotenuse of the triangle.
32 + (\(\sqrt{27}\))2 = c2
9 + 27 = c2
36 = c2
\(\sqrt{36}\) = \(\sqrt{c^{2}}\)
6 = c
The length of the hypotenuse of the right triangle is 6 ft.
Exercise 7.
The triangle shown below is an isosceles right triangle. Determine the length of the legs of the triangle. Show your work, and answer in a complete sentence.
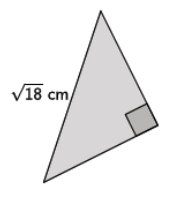
Answer:
Let x cm represent the length of each of the legs of the isosceles triangle.
x2 + x2 = (\(\sqrt{18}\))2
2x2 = 18
\(\frac{2 x^{2}}{2}\) = \(\frac{18}{2}\)
x2 = 9
\(\sqrt{x^{2}}\) = \(\sqrt{9}\)
x = 3
The leg lengths of the isosceles triangle are 3 cm.
Eureka Math Grade 8 Module 7 Lesson 16 Problem Set Answer Key
Question 1.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.
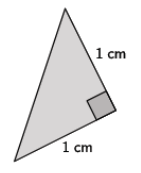
Answer:
Let c cm represent the length of the hypotenuse of the triangle.
12 + 12 = c2
1 + 1 = c2
2 = c2
\(\sqrt{2}\) = \(\sqrt{c^{2}}\)
1.4≈c
The length of the hypotenuse is exactly \(\sqrt{2}\) cm and approximately 1.4 cm.
Question 2.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.
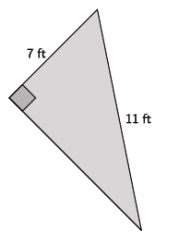
Answer:
Let x ft. represent the unknown length of the triangle.
72 + x2 = 112
49 + x2 = 121
49 – 49 + x2 = 121 – 49
x2 = 72
\(\sqrt{x^{2}}\) = \(\sqrt{72}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2}\) ⋅ \(\sqrt{3^{2}}\)
x = 6\(\sqrt{2}\)
x≈8.5
The length of the unknown side of the triangle is exactly 6\(\sqrt{2}\) ft. and approximately 8.5 ft.
Question 3.
Is the triangle with leg lengths of \(\sqrt{3}\) cm and 9 cm and hypotenuse of length \(\sqrt{84}\) cm a right triangle? Show your work, and answer in a complete sentence.
Answer:
(\(\sqrt{3}\))2 + 92 = (\(\sqrt{84}\))2
3 + 81 = 84
84 = 84
Yes, the triangle with leg lengths of \(\sqrt{3}\) cm and 9 cm and hypotenuse of length \(\sqrt{84}\) cm is a right triangle because the lengths satisfy the Pythagorean theorem.
Question 4.
Is the triangle with leg lengths of \(\sqrt{7}\) km and 5 km and hypotenuse of length \(\sqrt{48}\) km a right triangle? Show your work, and answer in a complete sentence.
Answer:
(\(\sqrt{7}\))2 + 52 = (\(\sqrt{48}\))2
7 + 25 = 48
32 ≠ 48
No, the triangle with leg lengths of \(\sqrt{7}\) km and 5 km and hypotenuse of length \(\sqrt{48}\) km is not a right triangle because the lengths do not satisfy the Pythagorean theorem.
Question 5.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.
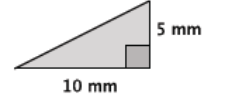
Answer:
Let c mm represent the length of the hypotenuse of the triangle.
52 + 102 = c2
25 + 100 = c2
125 = c2
\(\sqrt{125}\) = \(\sqrt{c^{2}}\)
\(\sqrt{5^{3}}\) = c
\(\sqrt{5^{2}}\)×\(\sqrt{5}\) = c
5\(\sqrt{5}\) = c
11.2≈c
The length of the hypotenuse is exactly 5\(\sqrt{5}\) mm and approximately 11.2 mm.
Question 6.
Is the triangle with leg lengths of 3 and 6 and hypotenuse of length \(\sqrt{45}\) a right triangle? Show your work, and answer in a complete sentence.
Answer:
32 + 62 = (\(\sqrt{45}\))2
9 + 36 = 45
45 = 45
Yes, the triangle with leg lengths of 3 and 6 and hypotenuse of length \(\sqrt{45}\) is a right triangle because the lengths satisfy the Pythagorean theorem.
Question 7.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.
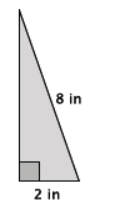
Answer:
Let x in. represent the unknown side length of the triangle.
22 + x2 = 82
4 + x2 = 64
4 – 4 + x2 = 64 – 4
x2 = 60
\(\sqrt{x^{2}}\) = \(\sqrt{60}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{3}\) ⋅ \(\sqrt{5}\)
x = 2\(\sqrt{15}\)
x≈7.7
The length of the unknown side of the triangle is exactly 2\(\sqrt{15}\) inches and approximately 7.7 inches.
Question 8.
Is the triangle with leg lengths of 1 and \(\sqrt{3}\) and hypotenuse of length 2 a right triangle? Show your work, and answer in a complete sentence.
Answer:
12 + (\(\sqrt{3}\))2 = 22
1 + 3 = 4
4 = 4
Yes, the triangle with leg lengths of 1 and \(\sqrt{3}\) and hypotenuse of length 2 is a right triangle because the lengths satisfy the Pythagorean theorem.
Question 9.
Corey found the hypotenuse of a right triangle with leg lengths of 2 and 3 to be \(\sqrt{13}\). Corey claims that since \(\sqrt{13}\) = 3.61 when estimating to two decimal digits, that a triangle with leg lengths of 2 and 3 and a hypotenuse of 3.61 is a right triangle. Is he correct? Explain.
Answer:
No, Corey is not correct.
22 + 32 = (3.61)2
4 + 9 = 13.0321
13 ≠ 13.0321
No, the triangle with leg lengths of 2 and 3 and hypotenuse of length 3.61 is not a right triangle because the lengths do not satisfy the Pythagorean theorem.
Question 10.
Explain a proof of the Pythagorean theorem.
Answer:
Consider having students share their proof with a partner while their partner critiques their reasoning. Accept any of the three proofs that students have seen.
Question 11.
Explain a proof of the converse of the Pythagorean theorem.
Answer:
Consider having students share their proof with a partner while their partner critiques their reasoning. Accept either of the proofs that students have seen.
Eureka Math Grade 8 Module 7 Lesson 16 Exit Ticket Answer Key
Question 1.
Is the triangle with leg lengths of 7 mm and 7 mm and a hypotenuse of length 10 mm a right triangle? Show your work, and answer in a complete sentence.
Answer:
72 + 72 = 102
49 + 49 = 100
98≠100
No, the triangle with leg lengths of 7 mm and 7 mm and hypotenuse of length 10 mm is not a right triangle because the lengths do not satisfy the Pythagorean theorem.
Question 2.
What would the length of the hypotenuse need to be so that the triangle in Problem 1 would be a right triangle? Show work that leads to your answer.
Answer:
Let c mm represent the length of the hypotenuse.
Then,
72 + 72 = c2
49 + 49 = c2
98 = c2
\(\sqrt{98}\) = c
The hypotenuse would need to be \(\sqrt{98}\) mm for the triangle with sides of 7 mm and 7 mm to be a right triangle.
Question 3.
If one of the leg lengths is 7 mm, what would the other leg length need to be so that the triangle in Problem 1 would be a right triangle? Show work that leads to your answer.
Answer:
Let a mm represent the length of one leg.
Then,
a2 + 72 = 102
a2 + 49 = 100
a2 + 49 – 49 = 100 – 49
a2 = 51
a = \(\sqrt{51}\)
The leg length would need to be \(\sqrt{51}\) mm so that the triangle with one leg length of 7 mm and the hypotenuse of 10 mm is a right triangle.