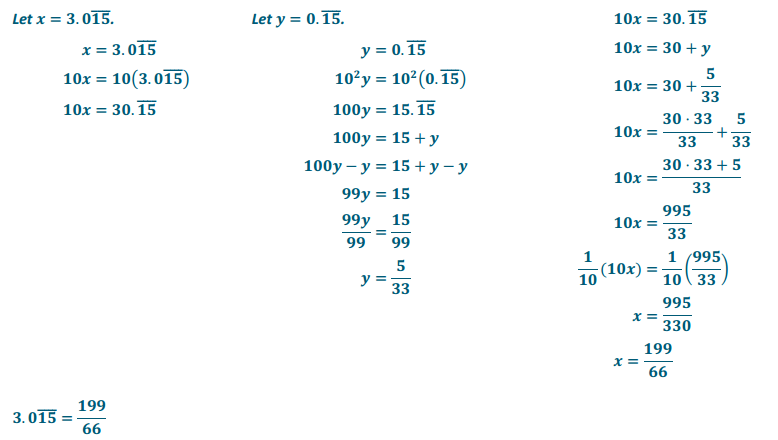Engage NY Eureka Math 8th Grade Module 7 Lesson 10 Answer Key
Eureka Math Grade 8 Module 7 Lesson 10 Example Answer Key
Example 1.
There is a fraction with an infinite decimal expansion of \(0 . \overline{81}\). Find the fraction.
Answer:
→ We want to find the fraction that is equal to the infinite decimal \(0 . \overline{81}\). Why might we want to write an infinite decimal as a fraction?
Maybe we want to use \(0 . \overline{81}\) in some calculation. It is unclear how to do arithmetic with infinitely long decimals. But if we recognize the decimal as a fraction, then we can do the arithmetic with
the fraction.
→ Let’s start by giving the decimal a name. Let x = \(0 . \overline{81}\) = 0.8181818181…. Any thoughts on what we might do to this number x? (Of course, our previous discussion was probably a hint!)
→ Allow students time to work in pairs or small groups to attempt to find the fraction equal to \(0 . \overline{81}\). Students should guess that multiplying x by some powers of 10 might yield something informative.
Let’s try multiplying x = \(0 . \overline{81}\) by some powers of 10.
x = 0.8181818181…
10x = 8.1818181…
100x = 81.81818181…
1000x = 818.1818181…
(Perhaps have students write x as \(\frac{8}{10} + \frac{1}{100} + \frac{8}{1000} + \frac{1}{10000} + \cdots\) to help with this process.)
Ask students to pause over the expression 100x. Can they observe anything interesting about it?
We see
100x = 81.81818181… = 81 + 0.818181… = 81 + x.
This now gives an equation for x students can solve.
100x = 81 + x
100x – x = 81 + x – x
(100 – 1)x = 81
99x = 81
\(\frac{99x}{99}\) = \(\frac{81}{99}\)
x = \(\frac{81}{99}\)
x = \(\frac{9}{11}\)
Therefore, the repeating decimal \(0 . \overline{81}\) = \(\frac{9}{11}\).
Have students use calculators to verify that this is correct.
Example 2.
Could it be that \(2.13 \overline{8}\) is also a fraction?
Answer:
→ We want to see if there is a fraction that is equal to the infinite decimal \(2.13 \overline{8}\). Notice that this time there is just one digit that repeats, but it is three places to the right of the decimal point.
→ Let’s multiply x = \(2.13 \overline{8}\) by various powers of 10 and see if any of the results seem helpful.
x = 2.138888…
10x = 21.38888…
100x = 213.8888…
1000x = 2138.888…
Do any of these seem helpful?
→ Students might not have any direct thoughts in response to this.
→ What if I asked as a separate question: Is 0.8888… the decimal expansion of a fraction? If knowing that 0.888… is a fraction, would any one of the equations we have then be of use to us?
If we know that 0.888… = \(\frac{a}{b}\), then we would see that 100x = 213 + 0.888… = 213 + \(\frac{a}{b}\). We could work out what x is from that.
Okay. As a side problem: Is 0.8888… the decimal expansion of some fraction?
Let y = \(0. \overline{8}\).
y = \(0. \overline{8}\)
10y = \(8. \overline{8}\)
10y = 8 + \(0. \overline{8}\)
10y = 8 + y
10y – y = 8 + y – y
9y = 8
\(\frac{9y}{9}\) = \(\frac{8}{9}\)
y = \(\frac{8}{9}\)
Now that we know that \(0. \overline{8}\) = \(\frac{8}{9}\), we will go back to our original problem.
100x = 213 + \(0. \overline{8}\)
100x = 213 + \(\frac{8}{9}\)
100x = \(\frac{213.9}{9}\) + \(\frac{8}{9}\)
100x = \(\frac{213.9 + 8}{9}\)
100x = \(\frac{1925}{9}\)
\(\frac{1}{100}\) (100x) = \(\frac{1}{100}\) (\(\frac{1925}{9}\))
x = \(\frac{1925}{900}\)
x = \(\frac{77}{36}\)
We can see that this technique applies to any infinite repeating decimal, even if there is a delay before the repeat begins, to show that every real number that has a repeating decimal expansion is, for sure, a rational number, that is, can be expressed as a fraction. And, conversely, we saw in Lesson 8 that every rational number has a repeating decimal expansion. So we have proven that the set of real numbers with repeating decimal expansions precisely matches the set of all rational numbers. Any number that has an infinitely long decimal expansion with no repeating pattern cannot be rational; that is, it must be an irrational number.
Eureka Math Grade 8 Module 7 Lesson 10 Exercise Answer Key
Exercises 1–2
Exercise 1.
There is a fraction with an infinite decimal expansion of \(0 . \overline{123}\). Let x = \(0 . \overline{123}\).
a. Explain why looking at 1000x helps us find the fractional representation of x.
Answer:
We have x = 0.123123123…, and we see that 1000x = 123.123123123…. This is the same as 123 + 0.123123123…, which is 123 + x. So we have the equation 1000x = 123 + x, which we can use to solve for x.
b. What is x as a fraction?
Answer:
1000x – x = 123 + x – x
999x = 123
\(\frac{999x}{999}\) = \(\frac{123}{999}\)
x = \(\frac{123}{999}\)
x = \(\frac{41}{333}\)
c. Is your answer reasonable? Check your answer using a calculator.
Answer:
Yes, my answer is reasonable and correct. It is reasonable because the denominator cannot be expressed as a product of 2’s and 5’s; therefore, I know that the fraction must represent an infinite decimal. It is also reasonable because the decimal value is closer to 0 than to 0.5, and the fraction \(\frac{41}{333}\) is also closer to 0 than to \(\frac{1}{2}\). It is correct because the division of \(\frac{41}{333}\) using a calculator is 0.123123….
Exercise 2.
There is a fraction with a decimal expansion of 0.4 ̅. Find the fraction, and check your answer using a calculator.
Answer:
Let x = \(0. \overline{4}\)
x = \(0 . \overline{4}\)
10x = (10)\(0 . \overline{4}\)
10x = \(4 . \overline{4}\)
10x = 4 + x
10x – x = 4 + x – x
9x = 4
\(\frac{9x}{9}\) = \(\frac{4}{9}\)
x = \(\frac{4}{9}\)
Exercises 3–4
Exercise 3.
Find the fraction equal to \(1.6 \overline{23}\). Check your answer using a calculator.
Answer:
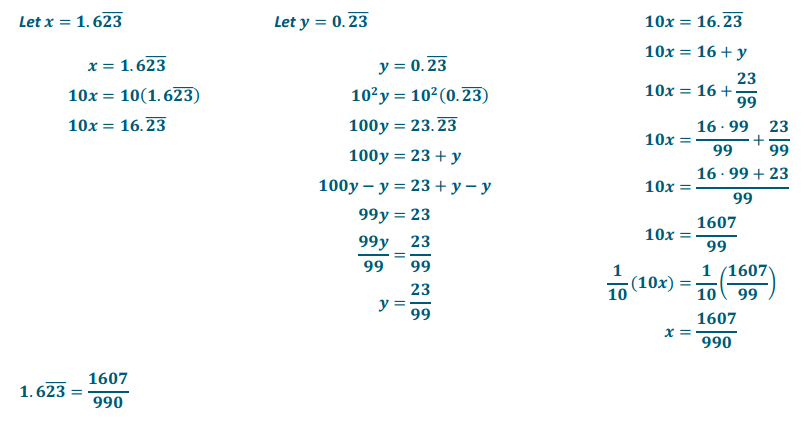
Exercise 4.
Find the fraction equal to \(2.9 \overline{60}\). Check your answer using a calculator.
Answer:
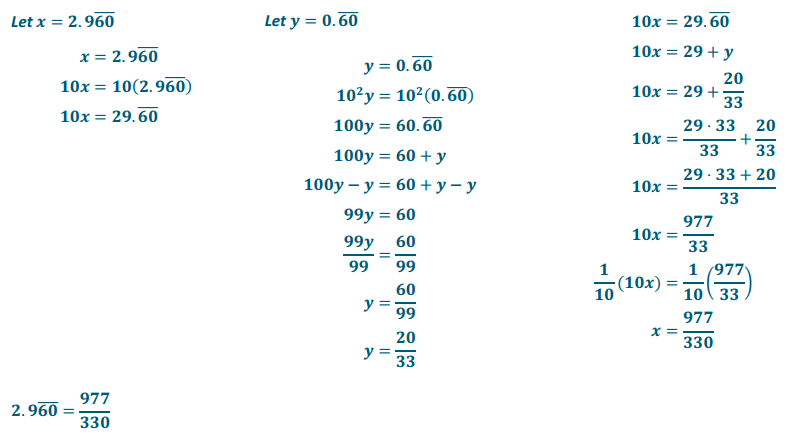
Eureka Math Grade 8 Module 7 Lesson 10 Problem Set Answer Key
Question 1.
a. Let x = \(0 . \overline{631}\). Explain why multiplying both sides of this equation by 103 will help us determine the fractional representation of x.
Answer:
When we multiply both sides of the equation by 103, on the right side we will have 631.631631…. This is helpful because we will now see this as 631 + x.
b. What fraction is x?
Answer:
1000x = \(631 . \overline{631}\)
1000x = 631 + 0.631631…
1000x = 631 + x
1000x – x = 631 + x – x
999x = 631
\(\frac{999x}{999}\) = \(\frac{631}{999}\)
x = \(\frac{631}{999}\)
c. Is your answer reasonable? Check your answer using a calculator.
Answer:
Yes, my answer is reasonable and correct. It is reasonable because the denominator cannot be expressed as a product of 2’s and 5’s; therefore, I know that the fraction must represent an infinite decimal. Also, the number 0.631 is closer to 0.5 than 1, and the fraction is also closer to \(\frac{1}{2}\) than 1. It is correct because the division of \(\frac{631}{999}\) using the calculator is 0.631631….
Question 2.
Find the fraction equal to \(3.40 \overline{8}\). Check your answer using a calculator.
Answer:
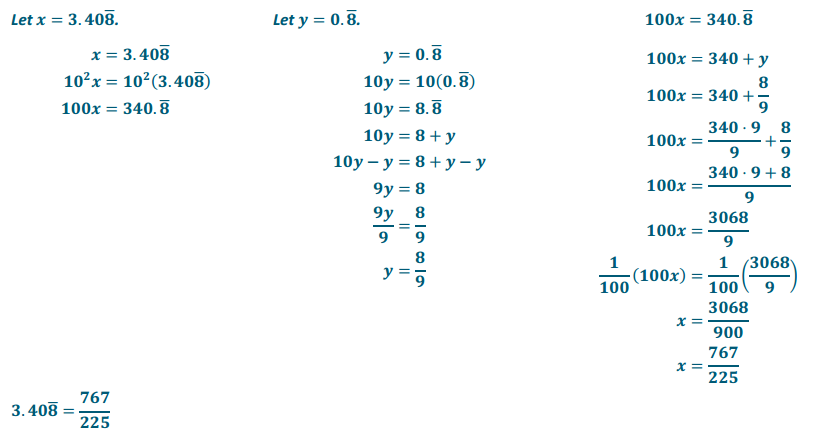
Question 3.
Find the fraction equal to \(0 . \overline{5923}\). Check your answer using a calculator.
Answer:
Let x = \(0 . \overline{5923}\).
x = \(0 . \overline{5923}\)
104 x = 104 (\(0 . \overline{5923}\) )
10000x = \(5923 . \overline{5923}\)
10000x = 5923 + x
10000x – x = 5923 + x – x
9999x = 5923
\(\frac{9999x}{9999}\) = \(\frac{5923}{9999}\)
x = \(\frac{5923}{9999}\)
Question 4.
Find the fraction equal to \(2.3 \overline{82}\). Check your answer using a calculator.
Answer:

Question 5.
Find the fraction equal to \(0 . \overline{714285}\). Check your answer using a calculator.
Answer:
Let x = \(0 . \overline{714285}\).
x = \(0 . \overline{714285}\)
106 x = 106 (\(0 . \overline{714285}\))
1 000 000x = \(714825 . \overline{714285}\)
1 000 000x = 714 285 + x
1 000000x – x = 714 285 + x – x
999 999x = 714 285
\(\frac{999999x}{999999}\) = \(\frac{714285}{9999999}\)
x = \(\frac{714285}{9999999}\)
x = \(\frac{5}{7}\)
Question 6.
Explain why an infinite decimal that is not a repeating decimal cannot be rational.
Answer:
We proved in Lesson 8 that the decimal expansion of any rational number must fall into a repeating cycle. (This came from performing the long division algorithm.) So any number that has an infinitely long decimal expansion that does not repeat cannot be a rational number; that is, it must be irrational.
Question 7.
In a previous lesson, we were convinced that it is acceptable to write \(0 . \overline{9}\) = 1. Use what you learned today to show that it is true.
Answer:
Let x = \(0 . \overline{9}\)
x = \(0 . \overline{9}\)
10x = 10(\(0 . \overline{9}\))
10x = \(9 . \overline{9}\)
10x = 9 + x
10x – x = 9 + x – x
9x = 9
\(\frac{9x}{9}\) = \(\frac{9}{9}\)
x = \(\frac{9}{9}\)
x = 1
Question 8.
Examine the following repeating infinite decimals and their fraction equivalents. What do you notice? Why do you think what you observed is true?
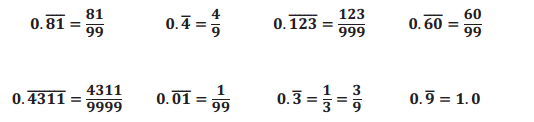
Answer:
In each case, the fraction that represents the infinite decimal has a numerator that is exactly the repeating part of the decimal and a denominator comprised of 9’s. Specifically, the denominator has the same number of digits of 9’s as the number of digits that repeat. For example, \(0 . \overline{81}\)has two repeating decimal digits, and the denominator has two 9’s.
The pattern is even true for \(0 . \overline{9}\). According to the pattern, this decimal equals \(\frac{9}{9}\), which is 1.
Eureka Math Grade 8 Module 7 Lesson 10 Exit Ticket Answer Key
Question 1.
Find the fraction equal to \(0 . \overline{534}\).
Answer:
Let x = \(0 . \overline{534}\).
x = \(0 . \overline{534}\)
103 x = 103 (\(0 . \overline{534}\) )
1000x = \(534 . \overline{534}\)
1000x = 534 + x
1000x – x = 534 + x – x
999x = 534
\(\frac{999x}{999}\) = \(\frac{534}{999}\)
x = \(\frac{534}{999}\)
x = \(\frac{178}{333}\)
\(0 . \overline{534}\)̅ = \(\frac{178}{333}\)
Question 2.
Find the fraction equal to \(3 . 0\overline{15}\).
Answer: