Engage NY Eureka Math 8th Grade Module 7 Lesson 1 Answer Key
Eureka Math Grade 8 Module 7 Lesson 1 Example Answer Key
Example 1.
Write an equation that allows you to determine the length of the unknown side of the right triangle.
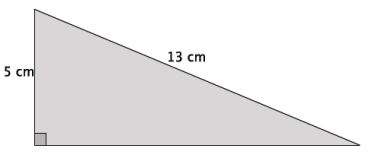
Answer:
Write an equation that allows you to determine the length of the unknown side of the right triangle.
Note: Students may use a different symbol to represent the unknown side length.
Let b cm represent the unknown side length. Then, 52 + b2 = 132.
Verify that students wrote the correct equation; then, allow them to solve it. Ask them how they knew the correct answer was 12. They should respond that 132-52 = 144, and since 144 is a perfect square, they knew that the unknown side length must be 12 cm.
Example 2.
Write an equation that allows you to determine the length of the unknown side of the right triangle.
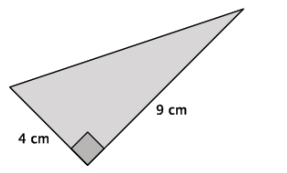
Answer:
→ Write an equation that allows you to determine the length of the unknown side of the right triangle.
Let c cm represent the length of the hypotenuse. Then, 42 + 92 = c2.
→ There is something different about this triangle. What is the length of the missing side? If you cannot find the length of the missing side exactly, then find a good approximation.
Provide students time to find an approximation for the length of the unknown side. Select students to share their answers and explain their reasoning. Use the points below to guide their thinking as needed.
→ How is this problem different from the last one?
The answer is c2 = 97. Since 97 is not a perfect square, the exact length cannot be represented as an integer.
→ Since 97 is not a perfect square, we cannot determine the exact length of the hypotenuse as an integer; however, we can make an estimate. Think about all of the perfect squares we have seen and calculated in past discussions. The number 97 is between which two perfect squares?
The number 97 is between 81 and 100.
If c2 were 81, what would be the length of the hypotenuse?
The length would be 9 cm.
If c2 were 100, what would be the length of the hypotenuse?
The length would be 10 cm.
→ At this point, we know that the length of the hypotenuse is somewhere between 9 cm and 10 cm. Think about the length to which it is closest. The actual length of the hypotenuse is determined by the equation c2 = 97. To which perfect square number, 100 or 81, is 97 closer?
The number 97 is closer to the perfect square 100 than to the perfect square 81.
→ Now that we know that the length of the hypotenuse of this right triangle is between 9 cm and 10 cm, but closer to 10 cm, let’s try to get an even better estimate of the length. Choose a number between 9 and 10 but closer to 10. Square that number. Do this a few times to see how close you can get to the number 97.
Provide students time to check a few numbers between 9 and 10. Students should see that the length is somewhere between 9.8 cm and 9.9 cm because 9.82 = 96.04 and 9.92 = 98.01. Some students may even check 9.85; 9.852 = 97.0225. This activity shows students that an estimation of the length being between 9 cm and 10 cm is indeed accurate, and it helps students develop an intuitive sense of how to estimate square roots.
Example 3.
Write an equation to determine the length of the unknown side of the right triangle.
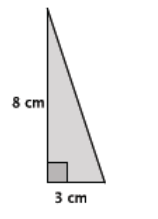
Answer:
→ Write an equation to determine the length of the unknown side of the right triangle.
Let c cm represent the length of the hypotenuse. Then, 32 + 82 = c2.
Verify that students wrote the correct equation, and then allow them to solve it. Instruct them to estimate the length, if necessary. Then, let them continue to work. When most students have finished, ask the questions below.
→ Could you determine an answer for the length of the hypotenuse as an integer?
No. Since c2 = 73, the length of the hypotenuse is not a perfect square.
Optionally, you can ask, “Can anyone find the exact length of the hypotenuse as a rational number?” It is important that students recognize that no one can determine the exact length of the hypotenuse as a rational number at this point.
→ Since 73 is not a perfect square, we cannot determine the exact length of the hypotenuse as a whole number. Let’s estimate the length. Between which two whole numbers is the length of the hypotenuse? Explain.
Since 73 is between the two perfect squares 64 and 81, we know the length of the hypotenuse must be between 8 cm and 9 cm.
→ Is the length closer to 8 cm or 9 cm? Explain.
The length is closer to 9 cm because 73 is closer to 81 than it is to 64.
→ The length of the hypotenuse is between 8 cm and 9 cm but closer to 9 cm.
Example 4.
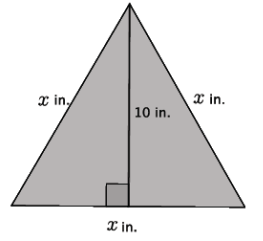
In the figure below, we have an equilateral triangle with a height of 10 Inches. What do we know about an equilateral triangle?
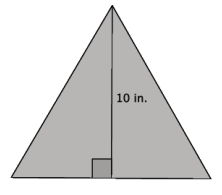
Answer:
→ In the figure below, we have an equilateral triangle with a height of 10 inches. What do we know about an equilateral triangle?
Equilateral triangles have sides that are all of the same length and angles that are all of the same degree, namely 60°.
Let’s say the length of the sides is x inches. Determine the approximate length of the sides of the triangle.
→ What we actually have here are two congruent right triangles.
Trace one of the right triangles on a transparency, and reflect it across the line representing the height of the triangle to convince students that an equilateral triangle is composed of two congruent right triangles.
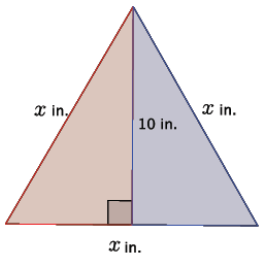
With this knowledge, we need to determine the length of the base of one of the right triangles. If we know that the length of the base of the equilateral triangle is x inches, then what is the length of the base of one of the right triangles? Explain.
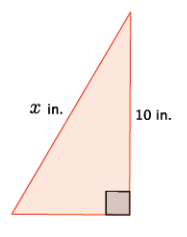
Eureka Math Grade 8 Module 7 Lesson 1 Exercise Answer Key
Exercise 1.
Use the Pythagorean theorem to find a whole number estimate of the length of the unknown side of the right triangle. Explain why your estimate makes sense.
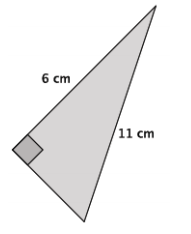
Answer:
Let x cm be the length of the unknown side.
62 + x2 = 112
36 + x2 = 121
x2 = 85
The length of the unknown side of the triangle is approximately 9 cm. The number 85 is between the perfect squares 81 and 100. Since 85 is closer to 81 than 100, then the length of the unknown side of the triangle is closer to 9 cm than it is to 10 cm.
Exercise 2.
Use the Pythagorean theorem to find a whole number estimate of the length of the unknown side of the right triangle. Explain why your estimate makes sense.
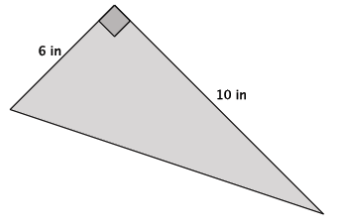
Answer:
Let c in. be the length of the hypotenuse.
62 + 102 = c2
36 + 100 = c2
136 = c2
The length of the hypotenuse is approximately 12 in. The number 136 is between the perfect squares 121 and 144. Since 136 is closer to 144 than 121, the length of the unknown side of the triangle is closer to 12 in. than it is to 11 in.
Exercise 3.
Use the Pythagorean theorem to find a whole number estimate of the length of the unknown side of the right triangle. Explain why your estimate makes sense.
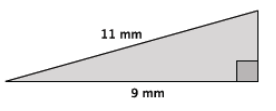
Answer:
Let x mm be the length of the unknown side.
92 + x2 = 112
81 + x2 = 121
x2 = 40
The length of the hypotenuse is approximately 6 mm. The number 40 is between the perfect squares 36 and 49. Since 40 is closer to 36 than 49, then the length of the unknown side of the triangle is closer to 6 mm than it is to 7 mm.
Eureka Math Grade 8 Module 7 Lesson 1 Problem Set Answer Key
Question 1.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.
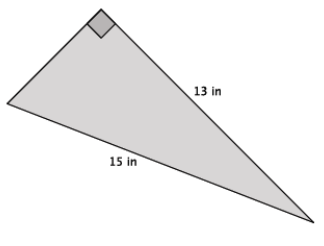
Answer:
Let x in. be the length of the unknown side.
132 + x2 = 152
169 + x2 = 225
x2 = 56
The number 56 is between the perfect squares 49 and 64. Since 56 is closer to 49 than it is to 64, the length of the unknown side of the triangle is closer to 7 in. than it is to 8 in.
Question 2.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.
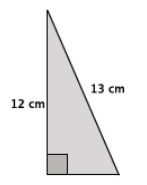
Answer:
Let x cm be the length of the unknown side.
x2 + 122 = 132
x2 + 144 = 169
x2 = 25
x = 5
The length of the unknown side is 5 cm. The Pythagorean theorem led me to the fact that the square of the value of the unknown length is 25. Since 25 is a perfect square, 25 is equal to 52; therefore, x = 5, and the unknown length of the triangle is 5 cm.
Question 3.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.
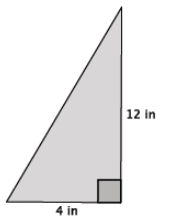
Answer:
Let c in. be the length of the hypotenuse.
42 + 122 = c2
16 + 144 = c2
160 = c2
The number 160 is between the perfect squares 144 and 169. Since 160 is closer to 169 than it is to 144, the length of the hypotenuse of the triangle is closer to 13 in. than it is to 12 in.
Question 4.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.
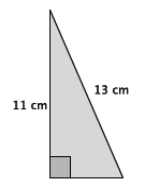
Answer:
Let x cm be the length of the unknown side.
x2 + 112 = 132
x2 + 121 = 169
x2 = 48
The number 48 is between the perfect squares 36 and 49. Since 48 is closer to 49 than it is to 36, the length of the unknown side of the triangle is closer to 7 cm than it is to 6 cm.
Question 5.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.
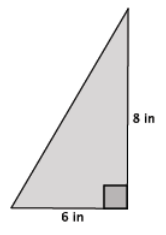
Answer:
Let c in. be the length of the hypotenuse.
62 + 82 = c2
36 + 64 = c2
100 = c2
10 = c
The length of the hypotenuse is 10 in. The Pythagorean theorem led me to the fact that the square of the value of the unknown length is 100. We know 100 is a perfect square, and 100 is equal to 102; therefore, c = 10, and the length of the hypotenuse of the triangle is 10 in.
Question 6.
Determine the length of the unknown side of the right triangle. Explain how you know your answer is correct.
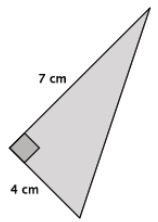
Answer:
Let c cm be the length of the hypotenuse.
72 + 42 = c2
49 + 16 = c2
65 = c2
The number 65 is between the perfect squares 64 and 81. Since 65 is closer to 64 than it is to 81, the length of the hypotenuse of the triangle is closer to 8 cm than it is to 9 cm.
Question 7.
Use the Pythagorean theorem to estimate the length of the unknown side of the right triangle. Explain why your estimate makes sense.
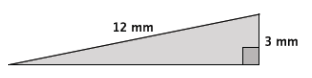
Answer:
Let x mm be the length of the unknown side.
32 + x2 = 122
9 + x2 = 144
x2 = 135
The number 135 is between the perfect squares 121 and 144. Since 135 is closer to 144 than it is to 121, the length of the unknown side of the triangle is closer to 12 mm than it is to 11 mm.
Question 8.
The triangle below is an isosceles triangle. Use what you know about the Pythagorean theorem to determine the approximate length of the base of the isosceles triangle.
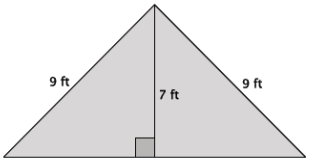
Answer:
Let x ft. represent the length of the base of one of the right triangles of the isosceles triangle.
x2 + 72 = 92
x2 + 49 = 81
x2 = 32
Since 32 is between the perfect squares 25 and 36 but closer to 36, the approximate length of the base of the right triangle is 6 ft. Since there are two right triangles, the length of the base of the isosceles triangle is approximately 12 ft.
Question 9.
Give an estimate for the area of the triangle shown below. Explain why it is a good estimate.
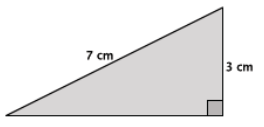
Answer:
Let x cm represent the length of the base of the right triangle.
x2 + 32 = 72
x2 + 9 = 49
x2 = 40
Since 40 is between the perfect squares 36 and 49 but closer to 36, the approximate length of the base is 6 cm.
A = \(\frac{1}{2}\)(6)(3) = 9
So, the approximate area of the triangle is 9 cm2. This is a good estimate because of the approximation of the length of the base. Further, since the hypotenuse is the longest side of the right triangle, approximating the length of the base as 6 cm makes mathematical sense because it has to be shorter than the hypotenuse.
Eureka Math Grade 8 Module 7 Lesson 1 Exit Ticket Answer Key
Question 1.
Determine the length of the unknown side of the right triangle. If you cannot determine the length exactly, then determine which two integers the length is between and the integer to which it is closest.
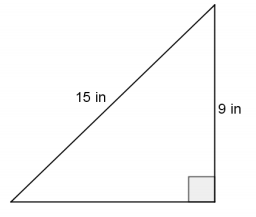
Answer:
Let x in. be the length of the unknown side.
92 + x2 = 152
81 + x2 = 225
x2 = 144
x = 12
The length of the unknown side is 12 in. The Pythagorean theorem led me to the fact that the square of the value of the unknown length is 144. We know 144 is a perfect square, and 144 is equal to 122; therefore, x = 12, and the unknown length of the triangle is 12 in.
Question 2.
Determine the length of the unknown side of the right triangle. If you cannot determine the length exactly, then determine which two integers the length is between and the integer to which it is closest.
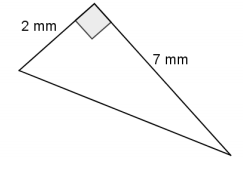
Answer:
Let x mm be the length of the unknown side.
22 + 72 = x2
4 + 49 = x2
53 = x2
The number 53 is between the perfect squares 49 and 64. Since 53 is closer to 49 than 64, the length of the unknown side of the triangle is closer to 7 mm than 8 mm.