Engage NY Eureka Math 8th Grade Module 6 Lesson 2 Answer Key
Eureka Math Grade 8 Module 6 Lesson 2 Example Answer Key
Example 1: Rate of Change and Initial Value
The equation of a line can be interpreted as defining a linear function. The graphs and the equations of lines are important in understanding the relationship between two types of quantities (represented in the following examples by x and y).
In a previous lesson, you encountered an MP3 download site that offers downloads of individual songs with the following price structure: a $3 fixed fee for a monthly subscription plus a fee of $0.25 per song. The linear function that models the relationship between the number of songs downloaded and the total monthly cost of downloading songs can be written as
y = 0.25x + 3,
where x represents the number of songs downloaded and y represents the total monthly cost (in dollars) for
MP3 downloads.
a. In your own words, explain the meaning of 0.25 within the context of the problem.
Answer:
In the example on the previous page, the value 0.25 means there is a cost increase of $0.25 for every 1 song downloaded.
b. In your own words, explain the meaning of 3 within the context of the problem.
Answer:
In the example on the previous page, the value of 3 represents an initial cost of $3 for downloading 0 songs. In other words, there is a fixed cost of $3 to subscribe to the site.
The values represented in the function can be interpreted in the following way:

Eureka Math Grade 8 Module 6 Lesson 2 Exercise Answer Key
Exercises 1–6: Is It a Better Deal?
Another site offers MP3 downloads with a different price structure: a $2 fixed fee for a monthly subscription plus a fee of $0.40 per song.
Exercise 1.
Write a linear function to model the relationship between the number of songs downloaded and the total monthly cost. As before, let x represent the number of songs downloaded and y represent the total monthly cost (in dollars) of downloading songs.
Answer:
y = 0.4x + 2
Exercise 2.
Determine the cost of downloading 0 songs and 10 songs from this site.
Answer:
y = 0.4(0) + 2 = 2.00. For 0 songs, the cost is $2.00.
y = 0.4(10) + 2 = 6.00. For 10 songs, the cost is $6.00.
Exercise 3.
The graph below already shows the linear model for the first subscription site (Company 1): y = 0.25x + 3. Graph the equation of the line for the second subscription site (Company 2) by marking the two points from your work in Exercise 2 (for 0 songs and 10 songs) and drawing a line through those two points.
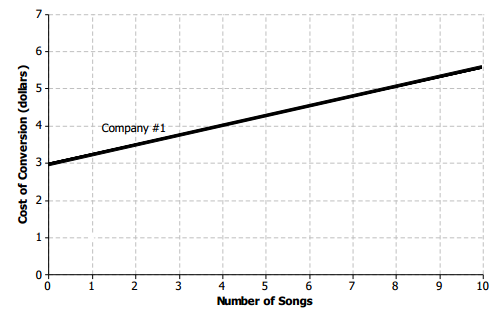
Answer:
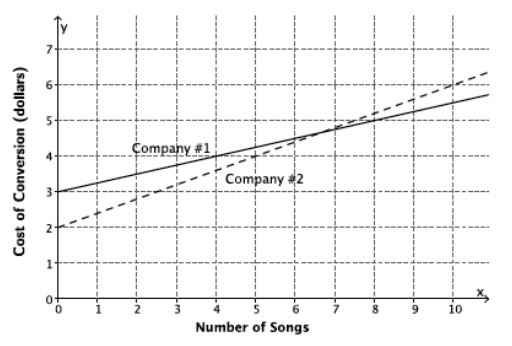
Exercise 4.
Which line has a steeper slope? Which company’s model has the more expensive cost per song?
Answer:
The line modeled by the second subscription site (Company 2) is steeper. It has the larger slope value and the greater cost per song.
Exercise 5.
Which function has the greater initial value?
Answer:
The first subscription site (Company 1) has the greater initial value. Its monthly subscription fee is $3 compared to only $2 for the second site.
Exercise 6.
Which subscription site would you choose if you only wanted to download 5 songs per month? Which company would you choose if you wanted to download 10 songs? Explain your reasoning.
Answer:
For 5 songs: Company 1’s cost is $4.25 (y = 25(5) + 3); Company 2’s cost is $4.00 (y = 0.4(5) + 2). So, Company 2 would be the better choice. Graphically, Company 2’s model also has the smaller y – value when x = 5.
For 10 songs: Company 1’s cost is $5.50 (y = 0.25(10) + 3); Company 2’s cost is $6.00 (y = 0.4(10) + 2). So, Company 1 would be the better choice. Graphically, Company 1’s model also has the smaller y – value at x = 10.
Exercises 7–9: Aging Autos
Exercise 7.
When someone purchases a new car and begins to drive it, the mileage (meaning the number of miles the car has traveled) immediately increases. Let x represent the number of years since the car was purchased and y represent the total miles traveled. The linear function that models the relationship between the number of years since purchase and the total miles traveled is y = 15000x.
a. Identify and interpret the rate of change.
Answer:
The rate of change is 15,000. It means that the mileage is increasing by 15,000 miles per year.
b. Identify and interpret the initial value.
Answer:
The initial value is 0. This means that there were no miles on the car when it was purchased.
c. Is the mileage increasing or decreasing each year according to the model? Explain your reasoning.
Answer:
Since the rate of change is positive, it means the mileage is increasing each year.
Exercise 8.
When someone purchases a new car and begins to drive it, generally speaking, the resale value of the car (in dollars) goes down each year. Let x represent the number of years since purchase and y represent the resale value of the car (in dollars). The linear function that models the resale value based on the number of years since purchase is
y = 20000 – 1200x.
a. Identify and interpret the rate of change.
Answer:
The rate of change is – 1,200. The resale value of the car is decreasing $1,200 every year since purchase.
b. Identify and interpret the initial value.
Answer:
The initial value is $20,000. The car’s value at the time of purchase was $20,000.
c. Is the resale value increasing or decreasing each year according to the model? Explain.
Answer:
The slope is negative. This means that the resale value decreases each year.
Exercise 9.
Suppose you are given the linear function y = 2.5x + 10.
a. Write a story that can be modeled by the given linear function.
Answer:
Answers will vary. I am ordering cupcakes for a birthday party. The bakery is going to charge $2.50 per cupcake in addition to a $10 decorating fee.
b. What is the rate of change? Explain its meaning with respect to your story.
Answer:
The rate of change is 2.5, which means that the cost increases $2.50 for every additional cupcake ordered.
c. What is the initial value? Explain its meaning with respect to your story.
Answer:
The initial value is 10, which in this story means that there is a flat fee of $10 to decorate the cupcakes.
Eureka Math Grade 8 Module 6 Lesson 2 Problem Set Answer Key
Question 1.
A rental car company offers the following two pricing methods for its customers to choose from for a
one – month rental:
Method 1: Pay $400 for the month, or
Method 2: Pay $0.30 per mile plus a standard maintenance fee of $35.
a. Construct a linear function that models the relationship between the miles driven and the total rental cost for Method 2. Let x represent the number of miles driven and y represent the rental cost (in dollars).
Answer:
y = 35 + 0.30x
b. If you plan to drive 1,100 miles for the month, which method would you choose? Explain your reasoning.
Answer:
Method 1 has a flat rate of $400 regardless of miles. Using Method 2, the cost would be $365
(y = 35 + 0.3(1100)). So, Method 2 would be preferred.
Question 2.
Recall from a previous lesson that Kelly wants to add new music to her MP3 player. She was interested in a monthly subscription site that offered its MP3 downloading service for a monthly subscription fee plus a fee per song. The linear function that modeled the total monthly cost in dollars (y) based on the number of songs downloaded (x) is
y = 5.25 + 0.30x.
The site has suddenly changed its monthly price structure. The linear function that models the new total monthly cost in dollars (y) based on the number of songs downloaded (x) is y = 0.35x + 4.50.
a. Explain the meaning of the value 4.50 in the new equation. Is this a better situation for Kelly than before?
Answer:
The initial value is 4.50 and means that the monthly subscription cost is now $4.50. This is lower than before, which is good for Kelly.
b. Explain the meaning of the value 0.35 in the new equation. Is this a better situation for Kelly than before?
Answer:
The rate of change is 0.35. This means that the cost is increasing by $0.35 for every song downloaded. This is more than the download cost for the original plan.
c. If you were to graph the two equations (old versus new), which line would have the steeper slope? What does this mean in the context of the problem?
Answer:
The slope of the new line is steeper because the new linear function has a greater rate of change. It means that the total monthly cost of the new plan is increasing at a faster rate per song compared to the cost of the old plan.
d. Which subscription plan provides the better value if Kelly downloads fewer than 15 songs per month?
Answer:
If Kelly were to download 15 songs, both plans will cost the same ($9.75). Therefore, the new plan is cheaper if Kelly downloads fewer than 15 songs.
Eureka Math Grade 8 Module 6 Lesson 2 Exit Ticket Answer Key
In 2008, a collector of sports memorabilia purchased 5 specific baseball cards as an investment. Let y represent each card’s resale value (in dollars) and x represent the number of years since purchase. Each card’s resale value after 0, 1, 2, 3, and 4 years could be modeled by linear equations as follows:
Card A: y = 5 – 0.7x
Card B: y = 4 + 2.6x
Card C: y = 10 + 0.9x
Card D: y = 10 – 1.1x
Card E: y = 8 + 0.25x
Question 1.
Which card(s) are decreasing in value each year? How can you tell?
Answer:
Cards A and D are decreasing in value, as shown by the negative values for rate of change in each equation.
Question 2.
Which card(s) had the greatest initial value at purchase (at 0 years)?
Answer:
Since all of the models are in slope – intercept form, Cards C and D have the greatest initial values at $10 each.
Question 3.
Which card(s) is increasing in value the fastest from year to year? How can you tell?
Answer:
Card B is increasing in value the fastest from year to year. Its model has the greatest rate of change.
Question 4.
If you were to graph the equations of the resale values of Card B and Card C, which card’s graph line would be steeper? Explain.
Answer:
The Card B line would be steeper because the function for Card B has the greatest rate of change; the card’s value is increasing at a faster rate than the other values of other cards.
Question 5.
Write a sentence explaining the 0.9 value in Card C’s equation.
Answer:
The 0.9 value means that Card C’s value increases by 90 cents per year.