Engage NY Eureka Math 8th Grade Module 6 Lesson 10 Answer Key
Eureka Math Grade 8 Module 6 Lesson 10 Exercise Answer Key
Example 1.
Predicting the value of a numerical dependent (response) variable based on the value of a given numerical independent variable has many applications in statistics. The first step in the process is to identify the dependent (predicted) variable and the independent (predictor) variable.
There may be several independent variables that might be used to predict a given dependent variable. For example, suppose you want to predict how well you are going to do on an upcoming statistics quiz. One possible independent variable is how much time you spent studying for the quiz. What are some other possible numerical independent variables that could relate to how well you are going to do on the quiz?
Exercises 1–2
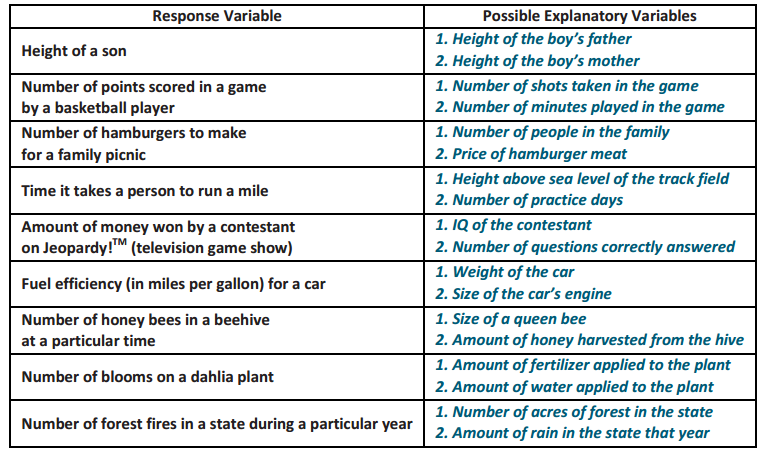
Exercise 1.
For each of the following dependent (response) variables, identify two possible numerical independent (explanatory) variables that might be used to predict the value of the dependent variable.
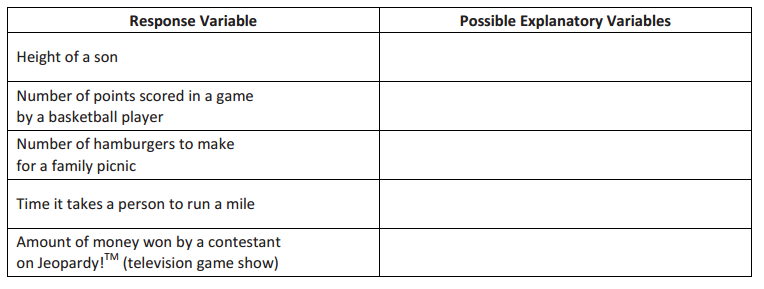
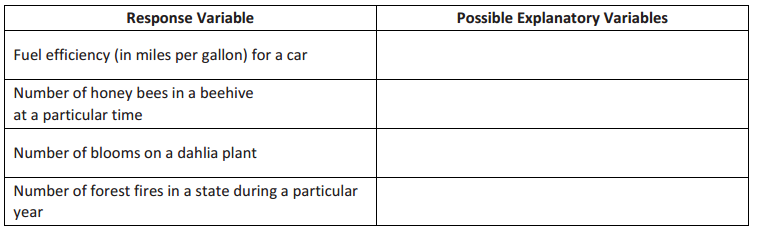
Answer:
Exercise 2.
Now, reverse your thinking. For each of the following numerical independent variables, write a possible numerical dependent variable.
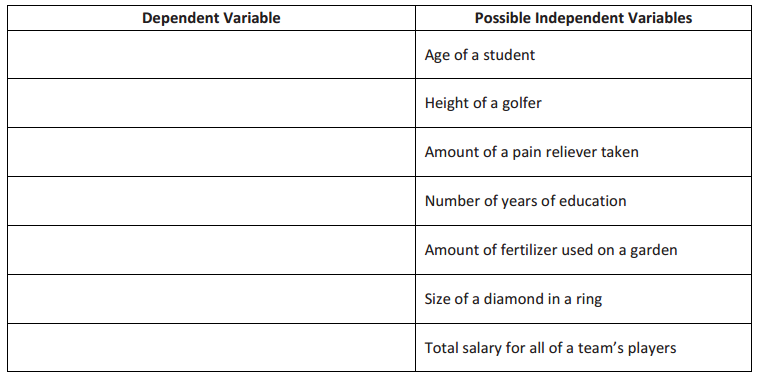
Answer:
Example 2.
A cell phone company offers the following basic cell phone plan to its customers: A customer pays a monthly fee of $40.00. In addition, the customer pays $0.15 per text message sent from the cell phone. There is no limit to the number of text messages per month that could be sent, and there is no charge for receiving text messages.
Exercises 3–11
Exercise 3.
Determine the following:
a. Justin never sends a text message. What would be his total monthly cost?
Answer:
Justin’s monthly cost would be $40.00.
b. During a typical month, Abbey sends 25 text messages. What is her total cost for a typical month?
Answer:
Abbey’s monthly cost would be $40.00 + $0.15(25), or $43.75.
c. Robert sends at least 250 text messages a month. What would be an estimate of the least his total monthly cost is likely to be?
Answer:
Robert’s monthly cost would be $40.00 + $0.15(250), or $77.50.
Exercise 4.
Use descriptive words to write a linear model describing the relationship between the number of text messages sent and the total monthly cost.
Answer:
Total monthly cost = $40.00 + (number of text messages) $0.15
Exercise 5.
Is the relationship between the number of text messages sent and the total monthly cost linear? Explain your answer.
Answer:
Yes. For each text message, the total monthly cost goes up by $0.15. From our previous work with linear functions, this would indicate a linear relationship.
Exercise 6.
Let x represent the independent variable and y represent the dependent variable. Use the variables x and y to write the function representing the relationship you indicated in Exercise 4.
Answer:
Students show the process in developing a model of the relationship between the two variables.
y = 0.15x + 40 or y = 40 + 0.15x
Exercise 7.
Explain what $0.15 represents in this relationship.
Answer:
$0.15 represents the slope of the linear relationship, or the change in the total monthly cost is $0.15 for an increase of one text message. (Students need to clearly explain that slope is the change in the dependent variable for a
1 – unit increase in the independent variable.)
Exercise 8.
Explain what $40.00 represents in this relationship.
Answer:
$40.00 represents the fixed monthly fee or the y – intercept of this relationship. This is the value of the total monthly cost when the number of text messages is 0.
Exercise 9.
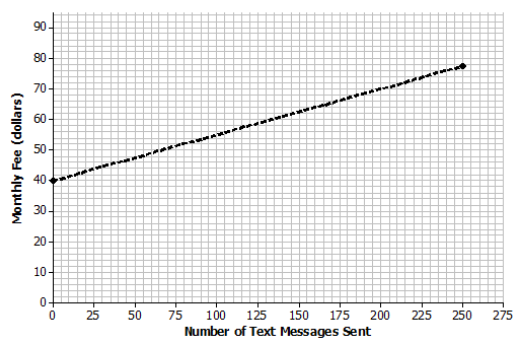
Sketch a graph of this relationship on the following coordinate grid. Clearly label the axes, and include units in the labels.
Answer:
Anticipated response: Students label the x – axis as the number of text messages. They label the y – axis as the total monthly cost. Students use any two points they derived in Exercise 3. The following graph uses the point of (0,40) for Justin and the point (250,77.5) for Robert. Highlight the intercept of (0,40), along with the slope of the line they sketched. Also, point out that the line students draw should be a dotted line (and not a solid line). The number of text messages can only be whole numbers, and as a result, the line representing this relationship should indicate that values in between the whole numbers representing the text messages are not part of the data.
Exercise 10.
LaMoyne needs four more pieces of lumber for his Scout project. The pieces can be cut from one large piece of lumber according to the following pattern.

The lumberyard will make the cuts for LaMoyne at a fixed cost of $2.25 plus an additional cost of 25 cents per cut. One cut is free.
a. What is the functional relationship between the total cost of cutting a piece of lumber and the number of cuts required? What is the equation of this function? Be sure to define the variables in the context of this problem.
Answer:
As students uncover the information in this problem, they should realize that the functional relationship between the total cost and number of cuts is linear. Noting that one cut is free, the equation could be written in one of the following ways:
Total cost for cutting = 2.25 + (0.25)(number of cuts – 1)
y = 2.25 + (0.25)(x – 1), where x is the number of cuts and y is the total cost for cutting
Total cost for cutting = 2 + (0.25)(number of cuts)
y = 2 + 0.25x, where x is the number of cuts and y is the total cost for cutting
Total cost for cutting = 2.25 + (0.25)(number of paid cuts)
y = 2.25 + 0.25x, where x is the number of paid cuts and y is the total cost for cutting
b. Use the equation to determine LaMoyne’s total cost for cutting.
Answer:
LaMoyne requires three cuts, one of which is free. Using any of the three forms given in part (a) yields a total cost for cutting of $2.75.
c. In the context of this problem, interpret the slope of the equation in words.
Answer:
Using any of the three forms, each additional cut beyond the free one adds $0.25 to the total cost for cutting.
d. Interpret the y – intercept of your equation in words in the context of this problem. Does interpreting the intercept make sense in this problem? Explain.
Answer:
If no cuts are required, then there is no fixed cost for cutting. So, it does not make sense to interpret the intercept in the context of this problem.
Exercise 11.
Omar and Olivia were curious about the size of coins. They measured the diameter and circumference of several coins and found the following data.
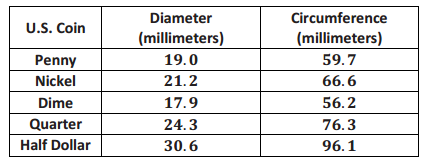
a. Wondering if there was any relationship between diameter and circumference, they thought about drawing a picture. Draw a scatter plot that displays circumference in terms of diameter.
Answer:
Students may need some help in deciding which is the independent variable and which is the dependent variable. Hopefully, they have seen from previous problems that whenever one variable, say variable A, is to be expressed in terms of some variable B, then variable A is the dependent variable, and variable B is the independent variable. So, circumference is being taken as the dependent variable in this problem, and diameter is being taken as the independent variable.
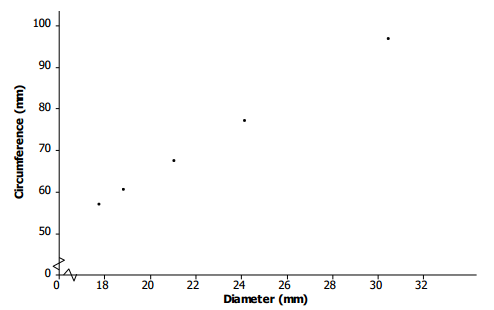
b. Do you think that circumference and diameter are related? Explain.
Answer:
It may be necessary to point out to students that because the data are rounded to one decimal place, the points on the scatter plot may not fall exactly on a line; however, they should. Circumference and diameter are linearly related.
c. Find the equation of the function relating circumference to the diameter of a coin.
Answer:
Again, because of a rounding error, equations that students find may be slightly different depending on which points they choose to do their calculations. Hopefully, they all arrive at something close to a circumference equal to 3.14, or π, multiplied by diameter.
For example, the slope of the line containing points (19,59.7) and (30.6,96.1) is \(\frac{96.1 – 59.7}{30.6 – 19}\) = 3.1379, which rounds to 3.14.
The intercept may be found using 59.7 = a + (3.14)(19.0), which yields a = 0.04, which rounds to 0.
Therefore, C = 3.14d + 0 = 3.14d.
d. The value of the slope is approximately equal to the value of π. Explain why this makes sense.
Answer:
The slope is identified as being approximately equal to π. (Note: Most students have previously studied the relationship between circumference and diameter of a circle. However, if students have not yet seen this result, discuss the interesting result that if the circumference of a circle is divided by its diameter, the result is a constant, namely, 3.14 rounded to two decimal places, no matter what circle is being considered.)
e. What is the value of the y – intercept? Explain why this makes sense.
Answer:
If the diameter of a circle is 0 (a point), then according to the equation, its circumference is 0. That is true, so interpreting the intercept of 0 makes sense in this problem.
Eureka Math Grade 8 Module 6 Lesson 10 Problem Set Answer Key
Question 1.
The Mathematics Club at your school is having a meeting. The advisor decides to bring bagels and his award – winning strawberry cream cheese. To determine his cost, from past experience he figures 1.5 bagels per student.
A bagel costs 65 cents, and the special cream cheese costs $3.85 and will be able to serve all of the anticipated students attending the meeting.
a. Find an equation that relates his total cost to the number of students he thinks will attend the meeting.
Answer:
Encourage students to write a problem in words in its context. For example, the advisor’s total cost = cream cheese fixed cost + cost of bagels. The cost of bagels depends on the unit cost of a bagel times the number of bagels per student times the number of students. So, with symbols, if c denotes the total cost in dollars and n denotes the number of students, then c = 3.85 + (0.65)(1.5)(n), or c = 3.85 + 0.975n.
b. In the context of the problem, interpret the slope of the equation in words.
Answer:
For each additional student, the cost goes up by 0.975 dollar, or 97.5 cents.
c. In the context of the problem, interpret the y – intercept of the equation in words. Does interpreting the intercept make sense? Explain.
Answer:
If there are no students, the total cost is $3.85. Students could interpret this by saying that the meeting was called off before any bagels were bought, but the advisor had already made his award – winning cream cheese, so the cost is $3.85. The intercept makes sense. Other students might argue otherwise.
Question 2.
John, Dawn, and Ron agree to walk/jog for 45 minutes. John has arthritic knees but manages to walk 1 \(\frac{1}{2}\) miles. Dawn walks 2 \(\frac{1}{4}\) miles, while Ron manages to jog 6 miles.
a. Draw an appropriate graph, and connect the points to show that there is a linear relationship between the distance that each traveled based on how fast each traveled (speed). Note that the speed for a person who travels 3 miles in 45 minutes, or \(\frac{3}{4}\) hour, is found using the expression 3 ÷ \(\frac{3}{4}\), which is 4 miles per hour.
Answer:
John’s speed is 2 miles per hour because 1 \(\frac{1}{2}\) ÷ \(\frac{3}{4}\) = 2. Dawn’s speed is 3 miles per hour because 2 \(\frac{1}{4}\) ÷ \(\frac{3}{4}\) = 3. Ron’s speed is 8 miles per hour because 6 ÷ \(\frac{3}{4}\) = 8. Students may draw the scatter plot incorrectly. Note that distance is to be expressed in terms of speed so that distance is the dependent variable on the vertical axis, and speed is the independent variable on the horizontal axis.
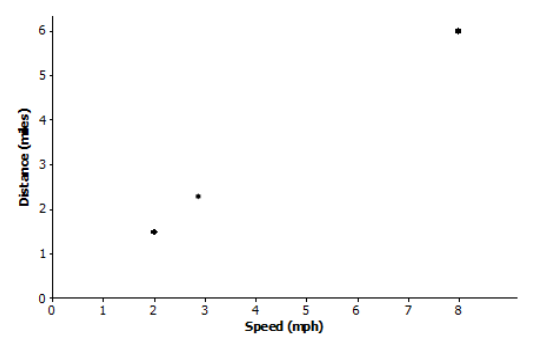
b. Find an equation that expresses distance in terms of speed (how fast one goes).
Answer:
The slope is \(\frac{6 – 1.5}{8 – 2}\) = 0.75, so the equation of the line through these points is
distance = a + (0.75)(speed).
Next, find the intercept. For example, solve 6 = a + (0.75)(8) for a, which yields a = 0.
So, the equation is distance = 0.75(speed).
c. In the context of the problem, interpret the slope of the equation in words.
Answer:
If someone increases her speed by 1 mile per hour, then that person travels 0.75 additional mile in 45 minutes.
d. In the context of the problem, interpret the y – intercept of the equation in words. Does interpreting the intercept make sense? Explain.
Answer:
The intercept of 0 makes sense because if the speed is 0 miles per hour, then the person is not moving.
So, the person travels no distance.
Question 3.
Simple interest is money that is paid on a loan. Simple interest is calculated by taking the amount of the loan and multiplying it by the rate of interest per year and the number of years the loan is outstanding. For college, Jodie’s older brother has taken out a student loan for $4,500 at an annual interest rate of 5.6%, or 0.056. When he graduates in four years, he has to pay back the loan amount plus interest for four years. Jodie is curious as to how much her brother has to pay.
a. Jodie claims that her brother has to pay a total of $5,508. Do you agree? Explain. As an example, a $1,200 loan has an 8% annual interest rate. The simple interest for one year is $96 because (0.08)(1,200) = 96. The simple interest for two years would be $192 because (2)(96) = 192.
Answer:
The total cost to repay = amount of the loan + interest on the loan.
Interest on the loan is the annual interest times the number of years the loan is outstanding.
The annual interest amount is (0.056)($4,500) = $252.
For four years, the simple interest amount is 4($252) = $1,008.
So, the total cost to repay the loan is $4,500 + $1,008 = $5,508. Jodie is right.
b. Write an equation for the total cost to repay a loan of $P if the rate of interest for a year is r (expressed as a decimal) for a time span of t years.
Answer:
Note: Work with students in identifying variables to represent the values discussed in this exercise. For example, the total cost to repay a loan is the amount of the loan plus the simple interest, or P + I, where P represents the amount of the loan and I represents the simple interest over t years.
The amount of interest per year is P times the annual interest. Let r represent the interest rate per year as a decimal.
The amount of interest per year is the amount of the loan, P, multiplied by the annual interest rate as a decimal, r (e.g., 5% is 0.05). The simple interest for t years, I, is the amount of interest per year multiplied by the number of years: I = (rt)P.
The total cost to repay the loan, c, is the amount of the loan plus the amount of simple interest; therefore, c = P + (rt)P.
c. If P and r are known, is the equation a linear equation?
Answer:
If P and r are known, then the equation should be written as c = P + (rP)t, which is the linear form where c is the dependent variable and t is the independent variable.
d. In the context of this problem, interpret the slope of the equation in words.
Answer:
For each additional year that the loan is outstanding, the total cost to repay the loan is increased by $rP.
As an example, consider Jodie’s brother’s equation for t years: c = 4500 + (0.056)(4500)t, or c = 4500 + 252t. For each additional year that the loan is not paid off, the total cost increases by $252.
e. In the context of this problem, interpret the y – intercept of the equation in words. Does interpreting the intercept make sense? Explain.
Answer:
The y – intercept is the value where t = 0. In this problem, it is the cost of the loan at the time that the loan was taken out. This makes sense because after 0 years, the cost to repay the loan would be $4,500, which is the amount of the original loan.
Eureka Math Grade 8 Module 6 Lesson 10 Exit Ticket Answer Key
Suppose that a cell phone monthly rate plan costs the user 5 cents per minute beyond a fixed monthly fee of $20.
This implies that the relationship between monthly cost and monthly number of minutes is linear.
Question 1.
Write an equation in words that relates total monthly cost to monthly minutes used. Explain how you found your answer.
Answer:
The equation is given by total monthly cost = 20 + 0.05 (number of minutes used for a month).
The y – intercept in the equation is the fixed monthly cost, $20.
The slope is the amount paid per minute of cell phone usage, or $0.05 per minute.
The linear form is total monthly cost = fixed cost + cost per minute (number of minutes used for a month).
Question 2.
Write an equation in symbols that relates the total monthly cost in dollars (y) to monthly minutes used (x).
Answer:
The equation is y = 20 + 0 .05x, where y is the total cost for a month in dollars and x is cell phone usage for the month in minutes.
Question 3.
What is the cost for a month in which 182 minutes are used? Express your answer in words in the context of this problem.
Answer:
20 + (0.05)(182) = 29.10
The total monthly cost in a month using 182 minutes would be $29.10.