Engage NY Eureka Math 8th Grade Module 5 Lesson 1 Answer Key
Eureka Math Grade 8 Module 5 Lesson 1 Example Answer Key
Example 1.
Suppose a moving object travels 256 feet in 4 seconds. Assume that the object travels at a constant speed, that is, the motion of the object can be described by a linear equation. Write a linear equation in two variables to represent the situation, and use the equation to predict how far the object has moved at the four times shown.
Answer:
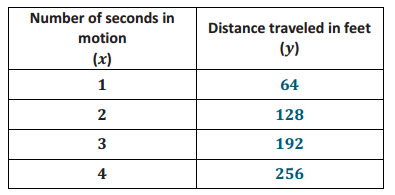
→ Suppose a moving object travels 256 feet in 4 seconds. Assume that the object travels at a constant speed, that is, the motion of the object can be described by a linear equation. Write a linear equation in two variables to represent the situation, and use the equation to predict how far the object has moved at the four times shown.
→ Let x represent the time it takes to travel y feet.
\(\frac{256}{4}\) = \(\frac{y}{x}\)
y = \(\frac{256}{4}\) x
y = 64x
→ What are some of the predictions that this equation allows us to make?
After one second, or when x = 1, the distance traveled is 64 feet.
Accept any reasonable predictions that students make.
→ Use your equation to complete the table.
→ What is the average speed of the moving object from 0 to 3 seconds?
The average speed is 64 feet per second. We know that the object has a constant rate of change; therefore, we expect the average speed to be the same over any time interval.
Example 2.
The object, a stone, is dropped from a height of 256 feet. It takes exactly 4 seconds for the stone to hit the ground. How far does the stone drop in the first 3 seconds? What about the last 3 seconds? Can we assume constant speed in this situation? That is, can this situation be expressed using a linear equation?
Answer:
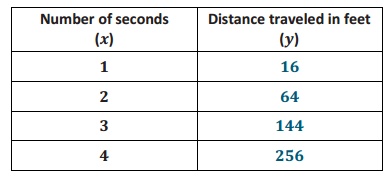
Provide students time to discuss this in pairs. Lead a discussion in which students share their thoughts with the class. It is likely they will say the motion of a falling object is linear and that the work conducted in the previous example is appropriate.
→ If this is a linear situation, then we predict that the stone drops 192 feet in the first 3 seconds.
Now consider viewing the 10-second “ball drop” video at the following link: http://www.youtube.com/watch?v = KrX_zLuwOvc. Consider showing it more than once.
→ If we were to slow the video down and record the distance the ball dropped after each second, here is the data we would obtain:
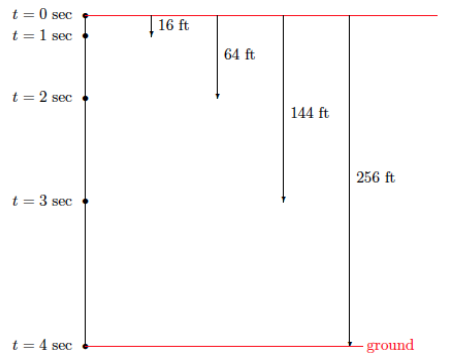
Have students record the data in the table of Example 2.
→ Was the linear equation developed in Example 1 appropriate after all?
Students who thought the stone was traveling at constant speed should realize that the predictions were not accurate for this situation. Guide their thinking using the discussion points below.
→ According to the data, how many feet did the stone drop in 3 seconds?
The stone dropped 144 feet.
→ How can that be? It must be that our initial assumption of constant rate was incorrect.
What predictions can we make now?
After one second, x = 1; the stone dropped 16 feet, etc.
→ Let’s make a prediction based on a value of x that is not listed in the table. How far did the stone drop in the first 3.5 seconds? What have we done in the past to figure something like this out?
Eureka Math Grade 8 Module 5 Lesson 1 Exercise Answer Key
Exercises 1–6
Use the table to answer Exercises 1–5.
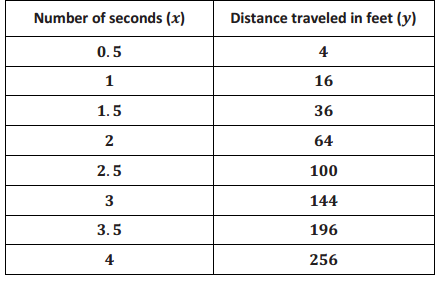
Exercise 1.
Name two predictions you can make from this table.
Answer:
Sample student responses:
After 2 seconds, the object traveled 64 feet. After 3.5 seconds, the object traveled 196 feet.
Exercise 2.
Name a prediction that would require more information.
Answer:
Sample student response:
We would need more information to predict the distance traveled after 3.75 seconds.
Exercise 3.
What is the average speed of the object between 0 and 3 seconds? How does this compare to the average speed calculated over the same interval in Example 1?
\(\text { Average Speed } = \frac{\text { distance traveled over a given time interval }}{\text { time interval }}\)
Answer:
The average speed is 48 feet per second: \(\frac{144}{3}\) = 48. This is different from the average speed calculated in Example 1. In Example 1, the average speed over an interval of 3 seconds was 64 feet per second.
Exercise 4.
Take a closer look at the data for the falling stone by answering the questions below.
a. How many feet did the stone drop between 0 and 1 second?
Answer:
The stone dropped 16 feet between 0 and 1 second.
b. How many feet did the stone drop between 1 and 2 seconds?
Answer:
The stone dropped 48 feet between 1 and 2 seconds.
c. How many feet did the stone drop between 2 and 3 seconds?
Answer:
The stone dropped 80 feet between 2 and 3 seconds.
d. How many feet did the stone drop between 3 and 4 seconds?
Answer:
The stone dropped 112 feet between 3 and 4 seconds.
e. Compare the distances the stone dropped from one time interval to the next. What do you notice?
Answer:
Over each interval, the difference in the distance was 32 feet. For example, 16+32 = 48, 48+32 = 80, and 80+32 = 112.
Exercise 5.
What is the average speed of the stone in each interval 0.5 second? For example, the average speed over the interval from 3.5 seconds to 4 seconds is
\(\frac{\text { distance traveled over a given time interval }}{\text { time interval }}\) = \(\frac{256-196}{4-3.5}\) = \(\frac{60}{0.5}\) = 120;120 feet per second
Repeat this process for every half-second interval. Then, answer the question that follows.
a. Interval between 0 and 0.5 second:
Answer:
\(\frac{4}{0.5}\) = 8;8 feet per second
b. Interval between 0.5 and 1 second:
Answer:
\(\frac{12}{0.5}\) = 24;24 feet per second
c. Interval between 1 and 1.5 seconds:
Answer:
\(\frac{20}{0.5}\) = 40;40 feet per second
d. Interval between 1.5 and 2 seconds:
Answer:
\(\frac{28}{0.5}\) = 56;56 feet per second
e. Interval between 2 and 2.5 seconds:
Answer:
\(\frac{36}{0.5}\) = 72;72 feet per second
f. Interval between 2.5 and 3 seconds:
Answer:
\(\frac{44}{0.5}\) = 88;88 feet per second
g. Interval between 3 and 3.5 seconds:
Answer:
\(\frac{52}{0.5}\) = 104;104 feet per second
h. Compare the average speed between each time interval. What do you notice?
Answer:
Over each interval, there is an increase in the average speed of 16 feet per second. For example, 8 + 16 = 24, 24 + 16 = 40, 40 + 16 = 56, and so on.
Exercise 6.
Is there any pattern to the data of the falling stone? Record your thoughts below.

Answer:
Accept any reasonable patterns that students notice as long as they can justify their claim. In the next lesson, students learn that y = 16t2.
Each distance has 16 as a factor. For example, 16 = 1(16), 64 = 4(16), 144 = 9(16), and 256 = 16(16).
Eureka Math Grade 8 Module 5 Lesson 1 Problem Set Answer Key
A ball is thrown across the field from point A to point B. It hits the ground at point B. The path of the ball is shown in the diagram below. The x-axis shows the horizontal distance the ball travels in feet, and the y-axis shows the height of the ball in feet. Use the diagram to complete parts (a)–(g).
Answer:
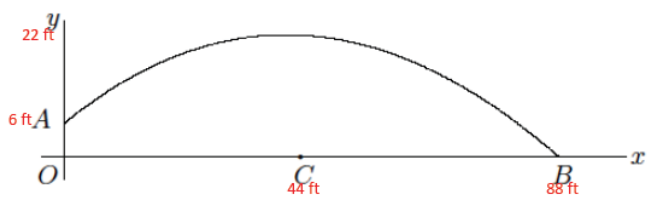
a. Suppose point A is approximately 6 feet above ground and that at time t = 0 the ball is at point A. Suppose the length of OB is approximately 88 feet. Include this information on the diagram.
Answer:
Information is noted on the diagram in red.
b. Suppose that after 1 second, the ball is at its highest point of 22 feet (above point C) and has traveled a horizontal distance of 44 feet. What are the approximate coordinates of the ball at the following values of t: 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, and 2.
Answer:
Most answers will vary because students are approximating the coordinates. The coordinates that must be correct because enough information was provided are denoted by a *.
At t = 0.25, the coordinates are approximately (11, 10).
At t = 0.5, the coordinates are approximately (22, 18).
At t = 0.75, the coordinates are approximately (33, 20).
*At t = 1, the coordinates are approximately (44, 22).
At t = 1.25, the coordinates are approximately (55, 19).
At t = 1.5, the coordinates are approximately (66, 14).
At t = 1.75, the coordinates are approximately (77, 8).
*At t = 2, the coordinates are approximately (88, 0).
c. Use your answer from part (b) to write two predictions.
Answer:
Sample predictions:
At a distance of 44 feet from where the ball was thrown, it is 22 feet in the air. At a distance of 66 feet from where the ball was thrown, it is 14 feet in the air.
d. What is happening to the ball when it has coordinates (88,0)?
Answer:
At point (88,0), the ball has traveled for 2 seconds and has hit the ground at a distance of 88 feet from where the ball began.
e. Why do you think the ball is at point (0, 6) when t = 0? In other words, why isn’t the height of the ball 0?
Answer:
The ball is thrown from point A to point B. The fact that the ball is at a height of 6 feet means that the person throwing it must have released the ball from a height of 6 feet.
f. Does the graph allow us to make predictions about the height of the ball at all points?
Answer:
While we cannot predict exactly, the graph allows us to make approximate predictions of the height for any value of horizontal distance we choose.
Eureka Math Grade 8 Module 5 Lesson 1 Exit Ticket Answer Key
Question 1.
A ball is bouncing across the school yard. It hits the ground at (0,0) and bounces up and lands at (1,0) and bounces again. The graph shows only one bounce.
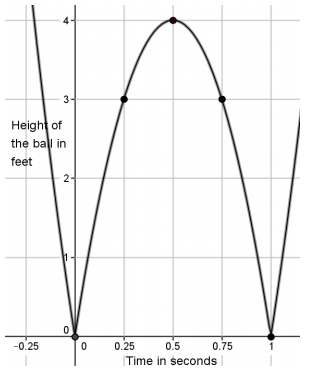
a. Identify the height of the ball at the following values of t: 0, 0.25, 0.5, 0.75, 1.
Answer:
When t = 0, the height of the ball is 0 feet above the ground. It has just hit the ground.
When t = 0.25, the height of the ball is 3 feet above the ground.
When t = 0.5, the height of the ball is 4 feet above the ground.
When t = 0.75, the height of the ball is 3 feet above the ground.
When t = 1, the height of the ball is 0 feet above the ground. It has hit the ground again.
b. What is the average speed of the ball over the first 0.25 seconds? What is the average speed of the ball over the next 0.25 seconds (from 0.25 to 0.5 seconds)?
Answer:
\(\frac{\text { distance traveled over a given time interval }}{\text { time interval }}\) = \(\frac{3-0}{0.25-0}\) = \(\frac{3}{0.25}\) = 12;12 feet per second
\(\frac{\text { distance traveled over a given time interval }}{\text { time interval }}\) = \(\frac{4-3}{0.5-0.25}\) = \(\frac{1}{0.25}\) = 4;4 feet per second
c. Is the height of the ball changing at a constant rate?
Answer:
No, it is not. If the ball were traveling at a constant rate, the average speed would be the same over any time interval.