Engage NY Eureka Math 8th Grade Module 4 Lesson 21 Answer Key
Eureka Math Grade 8 Module 4 Lesson 21 Example Answer Key
Example 1.
Let a line l be given in the coordinate plane. What linear equation is the graph of line l?
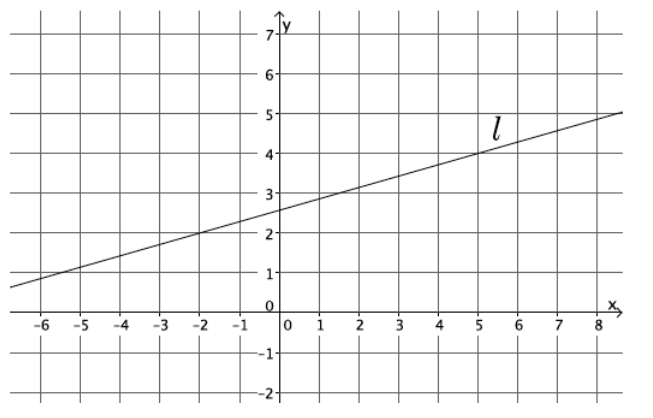
Answer:
We can pick two points to determine the slope, but the precise location of the y – intercept point cannot be determined from the graph.
Calculate the slope of the line.
Using points ( – 2, 2) and (5, 4), the slope of the line is
m = \(\frac{2 – 4}{ – 2 – 5}\)
= \(\frac{ – 2}{ – 7}\)
= \(\frac{2}{7}\)
→ Now we need to determine the y – intercept point of the line. We know that it is a point with coordinates (0, b), and we know that the line goes through points ( – 2, 2) and (5, 4) and has slope m = \(\frac{2}{7}\). Using this information, we can determine the coordinates of the y – intercept point and the value of b that we need in order to write the equation of the line.
→ Recall what it means for a point to be on a line; the point is a solution to the equation. In the equation y = mx + b, (x, y) is a solution, and m is the slope. Can we find the value of b? Explain.
Yes. We can substitute one of the points and the slope into the equation and solve for b.
→ Do you think it matters which point we choose to substitute into the equation? That is, will we get a different equation if we use the point ( – 2, 2) compared to (5, 4)?
No, because there can be only one line with a given slope that goes through a point.
→ Verify this claim by using m = \(\frac{2}{7}\) and ( – 2, 2) to find the equation of the line and then by using m = \(\frac{2}{7}\) and (5, 4) to see if the result is the same equation.
Sample student work:
2 = \(\frac{2}{7}\) ( – 2) + b
2 = – \(\frac{4}{7}\) + b
2 + \(\frac{4}{7}\) = – \(\frac{4}{7}\) + \(\frac{4}{7}\) + b
\(\frac{18}{7}\) = b
4 = \(\frac{2}{7}\) (5) + b
4 = \(\frac{10}{7}\) + b
4 – \(\frac{10}{7}\) = \(\frac{10}{7}\) – \(\frac{10}{7}\) + b
\(\frac{18}{7}\) = b
The y – intercept point is at (0, \(\frac{18}{7}\)), and the equation of the line is y = \(\frac{2}{7}\) x + \(\frac{18}{7}\).
→ The equation of the line is
y = \(\frac{2}{7}\) x + \(\frac{18}{7}\).
→ Write it in standard form.
Sample student work:
(y = \(\frac{2}{7}\) x + \(\frac{18}{7}\))7
7y = 2x + 18
– 2x + 7y = 2x – 2x + 18
– 2x + 7y = 18
– 1( – 2x + 7y = 18)
2x – 7y = – 18
Example 2.
Let a line l be given in the coordinate plane. What linear equation is the graph of line l?
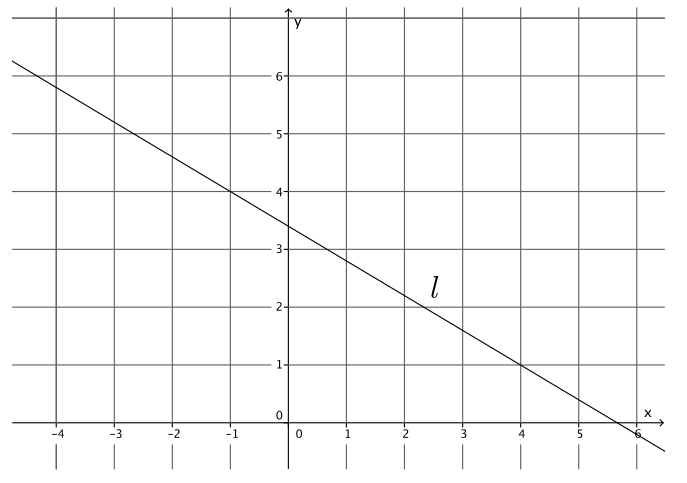
Answer:
Determine the slope of the line.
Using points ( – 1, 4) and (4, 1), the slope of the line is
m = \(\frac{4 – 1}{ – 1 – 4}\)
= \(\frac{3}{ – 5}\)
= – \(\frac{3}{5}\).
Determine the y – intercept point of the line.
Sample student work:
4 = ( – \(\frac{3}{5}\))( – 1) + b
4 = \(\frac{3}{5}\) + b
4 – \(\frac{3}{5}\) = \(\frac{3}{5}\) – \(\frac{3}{5}\) + b
\(\frac{17}{5}\) = b
The y – intercept point is at (0, \(\frac{17}{5}\)).
→ Now that we know the slope, m = – \(\frac{3}{5}\), and the y – intercept point, (0, \(\frac{17}{5}\)), write the equation of the line l in slope – intercept form.
y = – \(\frac{3}{5}\) x + \(\frac{17}{5}\)
→ Transform the equation so that it is written in standard form.
Sample student work:
y = – \(\frac{3}{5}\) x + \(\frac{17}{5}\)
(y = – \(\frac{3}{5}\) x + \(\frac{17}{5}\))5
5y = – 3x + 17
3x + 5y = – 3x + 3x + 17
3x + 5y = 17
Example 3.
Let a line l be given in the coordinate plane. What linear equation is the graph of line l?
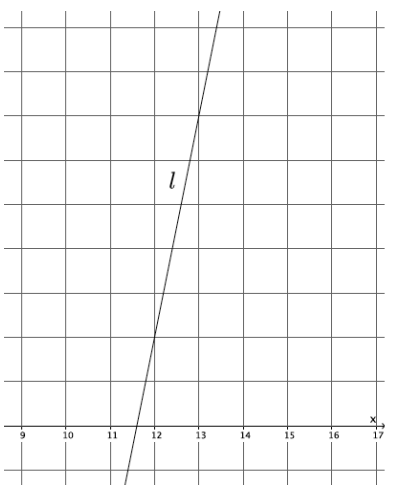
Answer:
→ Using points (12, 2) and (13, 7), the slope of the line is
m = \(\frac{2 – 7}{12 – 13}\)
= \(\frac{ – 5}{ – 1}\)
= 5.
→ Now, determine the y – intercept point of the line, and write the equation of the line in slope – intercept form.
Sample student work:
2 = 5(12) + b
2 = 60 + b
b = – 58
The y – intercept point is at (0, – 58), and the equation of the line is y = 5x – 58.
Now that we know the slope, m = 5, and the y – intercept point, (0, – 58), write the equation of the line l in standard form.
Sample student work:
y = 5x – 58
– 5x + y = 5x – 5x – 58
– 5x + y = – 58
– 1( – 5x + y = – 58)
5x – y = 58
Example 4.
Let a line l be given in the coordinate plane. What linear equation is the graph of line l?
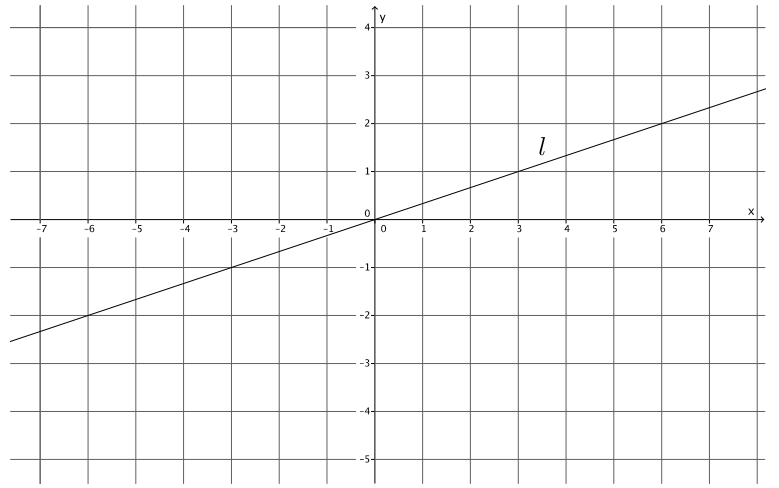
Answer:
Using points (3, 1) and ( – 3, – 1), the slope of the line is
m = \(\frac{ – 1 – 1}{ – 3 – 3}\)
= \(\frac{ – 2}{ – 6}\)
= \(\frac{1}{3}\)
The y – intercept point is at (0, 0), and the equation of the line is y = \(\frac{1}{3}\) x.
Eureka Math Grade 8 Module 4 Lesson 21 Exercise Answer Key
Exercises
Exercise 1.
Write the equation for the line l shown in the figure.
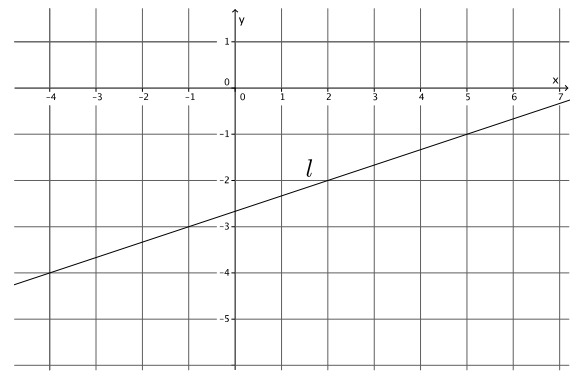
Answer:
Using the points ( – 1, – 3) and (2, – 2), the slope of the line is
m = \(\frac{ – 3 – ( – 2)}{ – 1 – 2}\)
= \(\frac{ – 1}{ – 3}\)
= \(\frac{1}{3}\) .
– 2 = \(\frac{1}{3}\) (2) + b
– 2 = \(\frac{2}{3}\) + b
– 2 – \(\frac{2}{3}\) = \(\frac{2}{3}\) – \(\frac{2}{3}\) + b
– \(\frac{8}{3}\) = b
The equation of the line is y = \(\frac{1}{3}\) x – \(\frac{8}{3}\).
Exercise 2.
Write the equation for the line l shown in the figure.
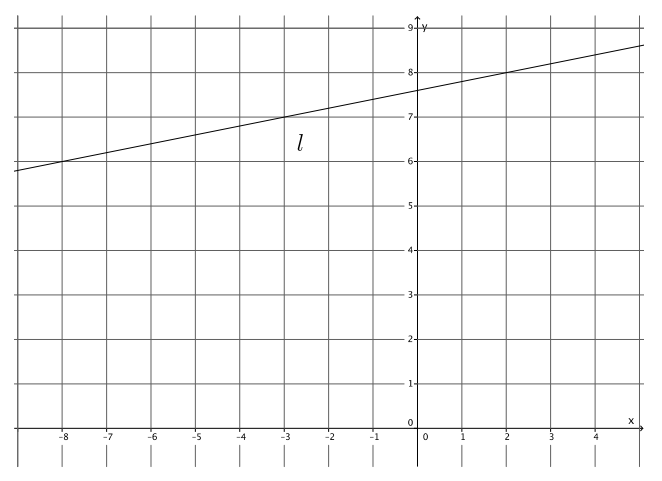
Answer:
Using the points ( – 3, 7) and (2, 8), the slope of the line is
m = \(\frac{7 – 8}{ – 3 – 2}\)
= \(\frac{ – 1}{ – 5}\)
= \(\frac{1}{5}\).
8 = \(\frac{1}{5}\) (2) + b
8 = \(\frac{2}{5}\) + b
8 – \(\frac{2}{5}\) = \(\frac{2}{5}\) – \(\frac{2}{5}\) + b
\(\frac{38}{5}\) = b
The equation of the line is y = \(\frac{1}{5}\) x + \(\frac{38}{5}\).
Exercise 3.
Determine the equation of the line that goes through points ( – 4, 5) and (2, 3).
Answer:
The slope of the line is
m = \(\frac{5 – 3}{ – 4 – 2}\)
= \(\frac{2}{ – 6}\)
= – \(\frac{1}{3}\)
The y – intercept point of the line is
3 = – \(\frac{1}{3}\) (2) + b
3 = – \(\frac{2}{3}\) + b
\(\frac{11}{3}\) = b.
The equation of the line is y = – \(\frac{1}{3}\) x + \(\frac{11}{3}\).
Exercise 4.
Write the equation for the line l shown in the figure.
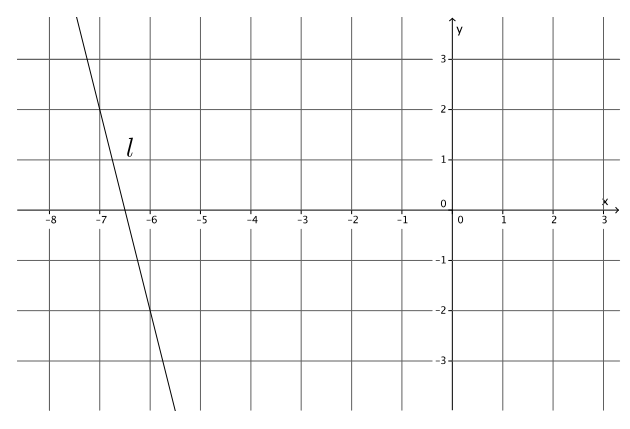
Answer:
Using the points ( – 7, 2) and ( – 6, – 2), the slope of the line is
m = \(\frac{2 – ( – 2)}{ – 7 – ( – 6)}\)
= \(\frac{4}{ – 1}\)
= – 4.
– 2 = – 4( – 6) + b
– 2 = 24 + b
– 26 = b
The equation of the line is y = – 4x – 26.
Exercise 5.
A line goes through the point (8, 3) and has slope m = 4. Write the equation that represents the line.
Answer:
3 = 4(8) + b
3 = 32 + b
– 29 = b
The equation of the line is y = 4x – 29.
Eureka Math Grade 8 Module 4 Lesson 21 Problem Set Answer Key
Question 1.
Write the equation for the line l shown in the figure.
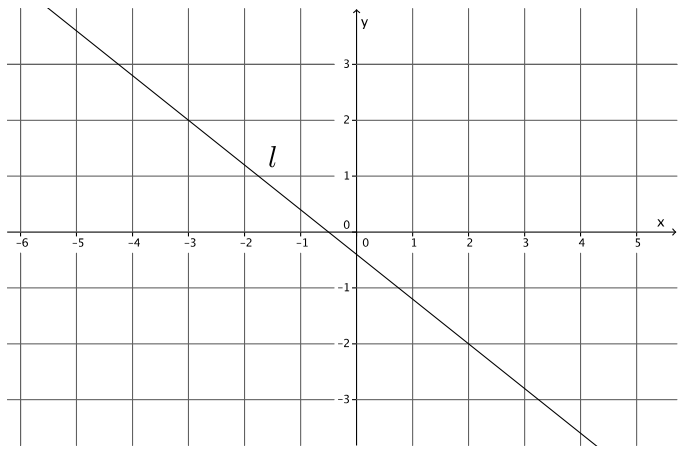
Answer:
Using the points ( – 3, 2) and (2, – 2), the slope of the line is
m = \(\frac{2 – ( – 2)}{ – 3 – 2}\)
= \(\frac{4}{ – 5}\)
= – \(\frac{4}{5}\)
2 = ( – \(\frac{4}{5}\))( – 3) + b
2 = \(\frac{12}{5}\) + b
2 – \(\frac{12}{5}\) = \(\frac{12}{5}\) – \(\frac{12}{5}\) + b
– \(\frac{2}{5}\) = b
The equation of the line is y = – \(\frac{4}{5}\) x – \(\frac{2}{5}\).
Question 2.
Write the equation for the line l shown in the figure.
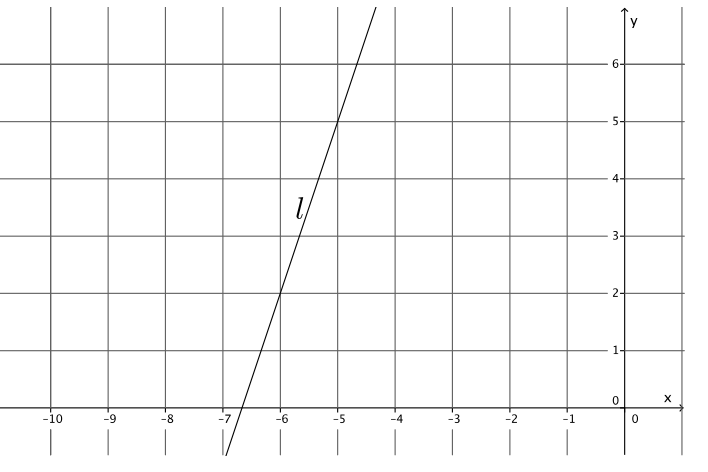
Answer:
Using the points ( – 6, 2) and ( – 5, 5), the slope of the line is
m = \(\frac{2 – 5}{ – 6 – ( – 5)}\)
= \(\frac{ – 3}{ – 1}\)
= 3.
5 = 3( – 5) + b
5 = – 15 + b
20 = b
The equation of the line is y = 3x + 20.
Question 3.
Write the equation for the line l shown in the figure.
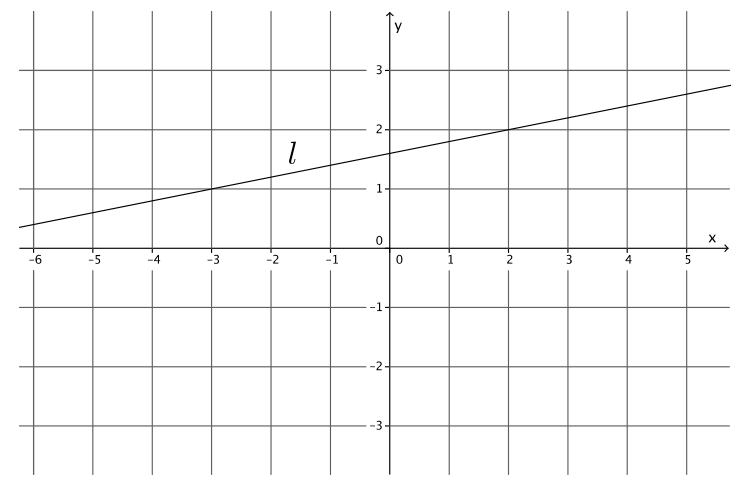
Answer:
Using the points ( – 3, 1) and (2, 2), the slope of the line is
m = \(\frac{1 – 2}{ – 3 – 2}\)
= \(\frac{ – 1}{ – 5}\)
= \(\frac{1}{5}\)
2 = \(\frac{1}{5}\) (2) + b
2 = \(\frac{2}{5}\) + b
2 – \(\frac{2}{5}\) = \(\frac{2}{5}\) – \(\frac{2}{5}\) + b
\(\frac{8}{5}\) = b
The equation of the line is y = \(\frac{1}{5}\) x + \(\frac{8}{5}\).
Question 4.
Triangle ABC is made up of line segments formed from the intersection of lines LAB, LBC, and LAC. Write the equations that represent the lines that make up the triangle.
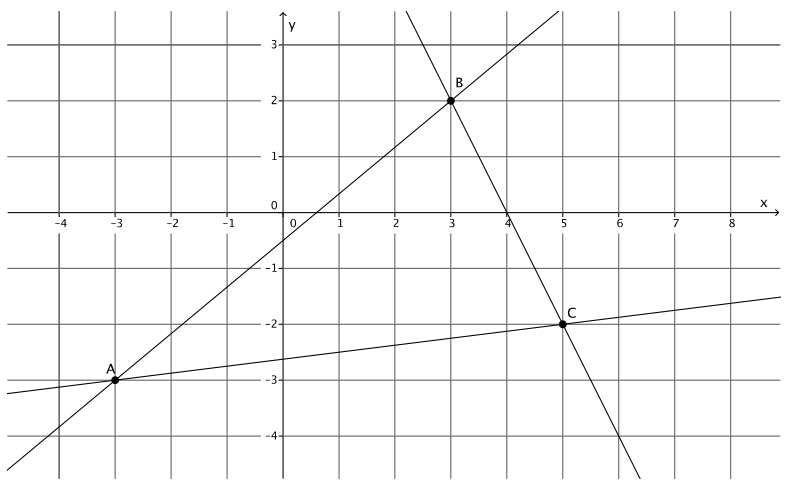
Answer:
A( – 3, – 3), B(3, 2), C(5, – 2)
The slope of LAB:
m = \(\frac{ – 3 – 2}{ – 3 – 3}\)
= \(\frac{ – 5}{ – 6}\)
= \(\frac{5}{6}\)
2 = \(\frac{5}{6}\) (3) + b
2 = \(\frac{5}{2}\) + b
2 – \(\frac{5}{2}\) = \(\frac{5}{2}\) – \(\frac{5}{2}\) + b
– \(\frac{1}{2}\) = b
The equation of LAB is y = \(\frac{5}{6}\) x – \(\frac{1}{2}\).
The slope of LBC:
m = \( = \frac{2 – ( – 2)}{3 – 5}\)
= \(\frac{4}{ – 2}\)
= – 2
2 = – 2(3) + b
2 = – 6 + b
8 = b
The equation of LBC is y = – 2x + 8.
The slope of LAC:
m = \(\frac{ – 3 – ( – 2)}{ – 3 – 5}\)
= \(\frac{ – 1}{ – 8}\)
= \(\frac{1}{8}\)
– 2 = \(\frac{1}{8}\) (5) + b
– 2 = \(\frac{5}{8}\) + b
– 2 – \(\frac{5}{8}\) = \(\frac{5}{8}\) – \(\frac{5}{8}\) + b
– 2\(\frac{1}{8}\) = b
The equation of LAC is y = \(\frac{1}{8}\) x – 2\(\frac{1}{8}\).
Question 5.
Write the equation for the line that goes through point ( – 10, 8) with slope m = 6.
Answer:
8 = 6( – 10) + b
8 = – 60 + b
68 = b
The equation of the line is y = 6x + 68.
Question 6.
Write the equation for the line that goes through point (12, 15) with slope m = – 2.
Answer:
15 = – 2(12) + b
15 = – 24 + b
39 = b
The equation of the line is y = – 2x + 39.
Question 7.
Write the equation for the line that goes through point (1, 1) with slope m = – 9.
Answer:
1 = – 9(1) + b
1 = – 9 + b
10 = b
The equation of the line is y = – 9x + 10.
Question 8.
Determine the equation of the line that goes through points (1, 1) and (3, 7).
Answer:
The slope of the line is
m = \(\frac{1 – 7}{1 – 3}\)
= \(\frac{ – 6}{ – 2}\)
= 3.
The y – intercept point of the line is
7 = 3(3) + b
7 = 9 + b
– 2 = b.
The equation of the line is y = 3x – 2.
Eureka Math Grade 8 Module 4 Lesson 21 Exit Ticket Answer Key
Question 1.
Write the equation for the line l shown in the figure below.
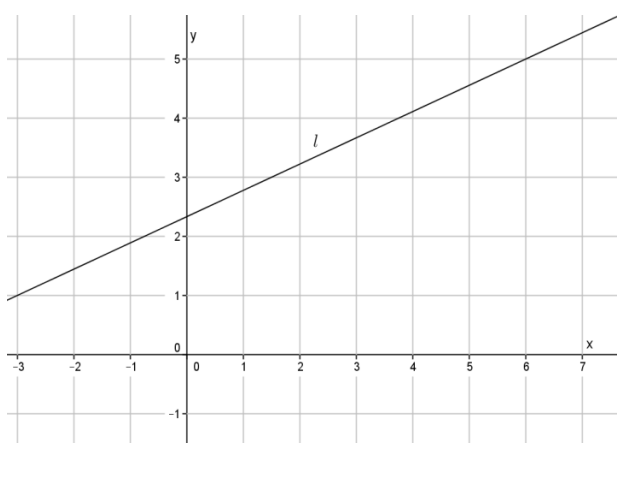
Answer:
Using the points ( – 3, 1) and (6, 5), the slope of the line is
m = \(\frac{5 – 1}{6 – ( – 3)}\)
m = \(\frac{4}{9}\)
5 = \(\frac{4}{9}\) (6) + b
5 = \(\frac{8}{3}\) + b
5 – \(\frac{8}{3}\) = \(\frac{8}{3}\) – \(\frac{8}{3}\) + b
\(\frac{7}{3}\) = b
The equation of the line is y = \(\frac{4}{9}\) x + \(\frac{7}{3}\).
Question 2.
A line goes through the point (5, – 7) and has slope m = – 3. Write the equation that represents the line.
Answer:
– 7 = – 3(5) + b
– 7 = – 15 + b
8 = b
The equation of the line is y = – 3x + 8.