Engage NY Eureka Math 8th Grade Module 4 Lesson 20 Answer Key
Eureka Math Grade 8 Module 4 Lesson 20 Exercise Answer Key
Opening Exercise
Figure 1
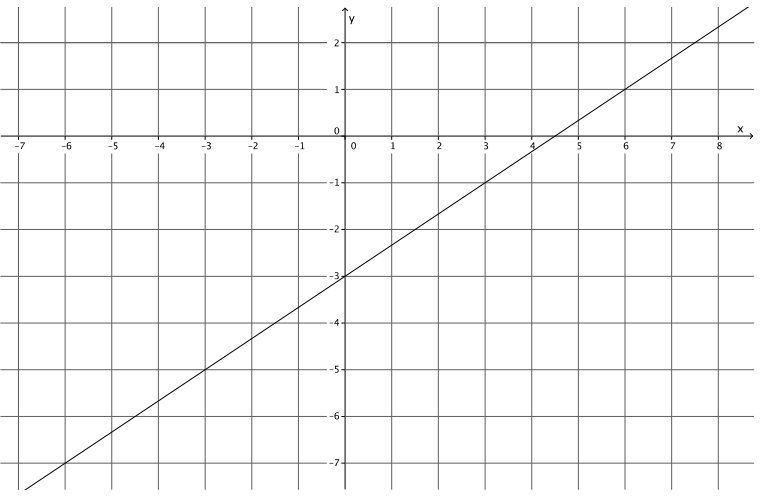
Answer:
The equation for the line in Figure 1 is y = \(\frac{2}{3}\) x – 3.
Figure 2
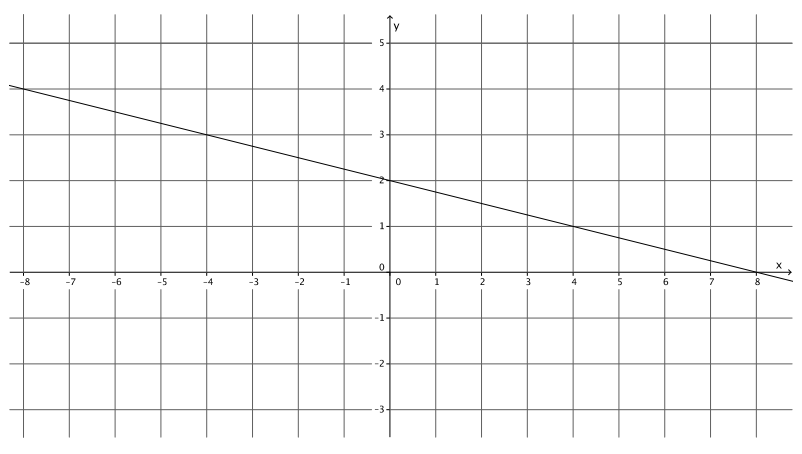
Answer:
The equation for the line in Figure 2 is y = – \(\frac{1}{4}\) x + 2.
Exercises
Exercise 1.
Write the equation that represents the line shown.
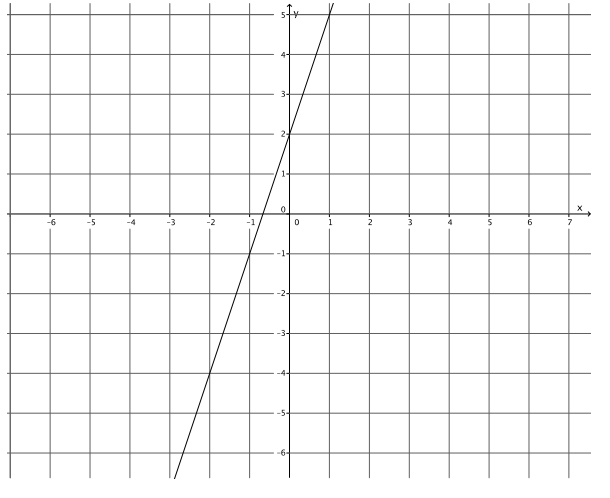
Answer:
y = 3x + 2
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = 3x + 2
– 3x + y = 3x – 3x + 2
– 3x + y = 2
– 1( – 3x + y = 2)
3x – y = – 2
Exercise 2.
Write the equation that represents the line shown.
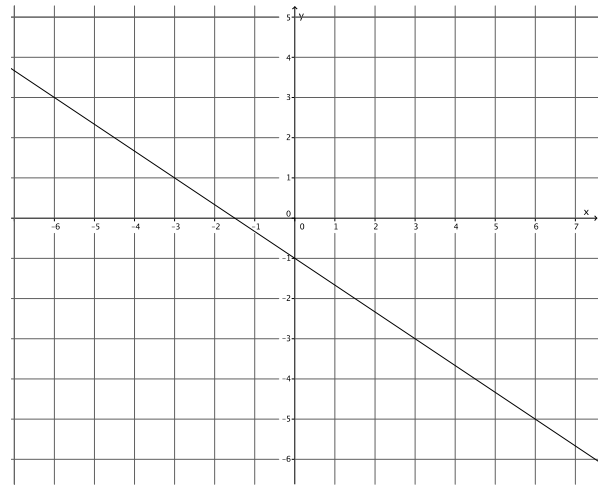
Answer:
y = – \(\frac{2}{3}\) x – 1
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and 𝒂 is not negative.
Answer:
y = – \(\frac{2}{3}\) x – 1
(y = – \(\frac{2}{3}\) x – 1)3
3y = – 2x – 3
2x + 3y = – 2x + 2x – 3
2x + 3y = – 3
Exercise 3.
Write the equation that represents the line shown.
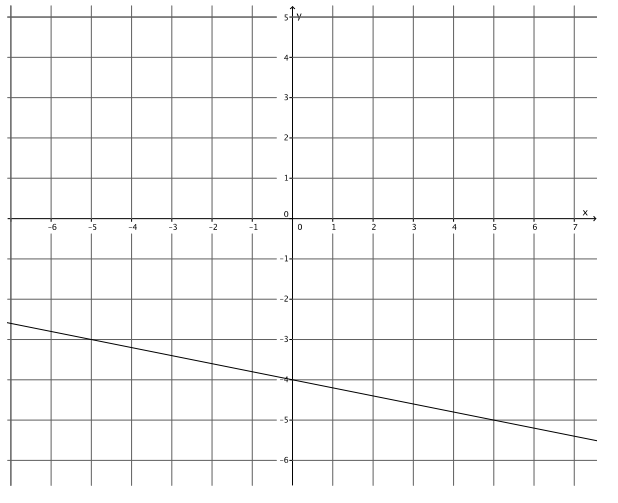
Answer:
y = – \(\frac{1}{5}\) x – 4
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = – \(\frac{1}{5}\) x – 4
(y = – \(\frac{1}{5}\) x – 4) 5
5y = – x – 20
x + 5y = – x + x – 20
x + 5y = – 20
x + 5
Exercise 4.
Write the equation that represents the line shown.
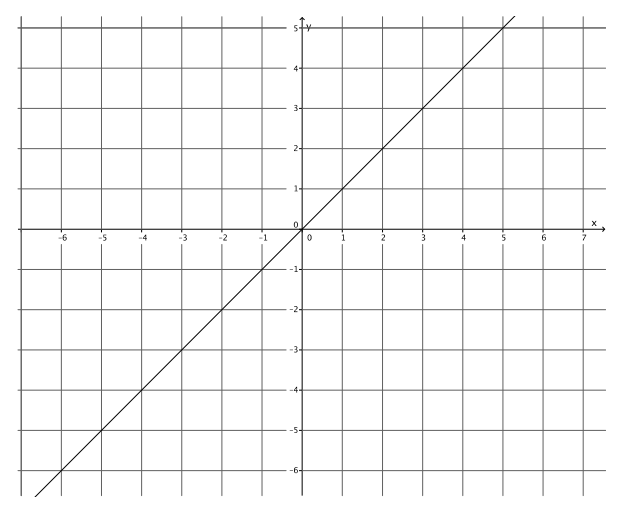
Answer:
y = x
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = x
– x + y = x – x
– x + y = 0
– 1( – x + y = 0)
x – y = 0
Exercise 5.
Write the equation that represents the line shown.
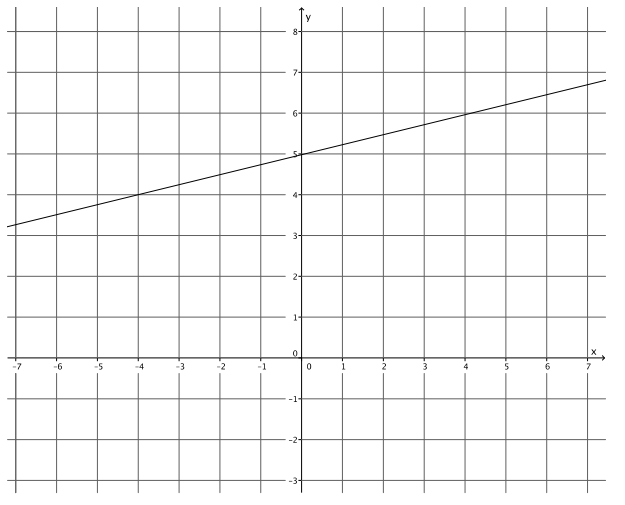
Answer:
y = \(\frac{1}{4}\) x + 5
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = \(\frac{1}{4}\) x + 5
(y = \(\frac{1}{4}\) x + 5)4
4y = x + 20
– x + 4y = x – x + 20
– x + 4y = 20
– 1( – x + 4y = 20)
x – 4y = – 20
Exercise 6.
Write the equation that represents the line shown.
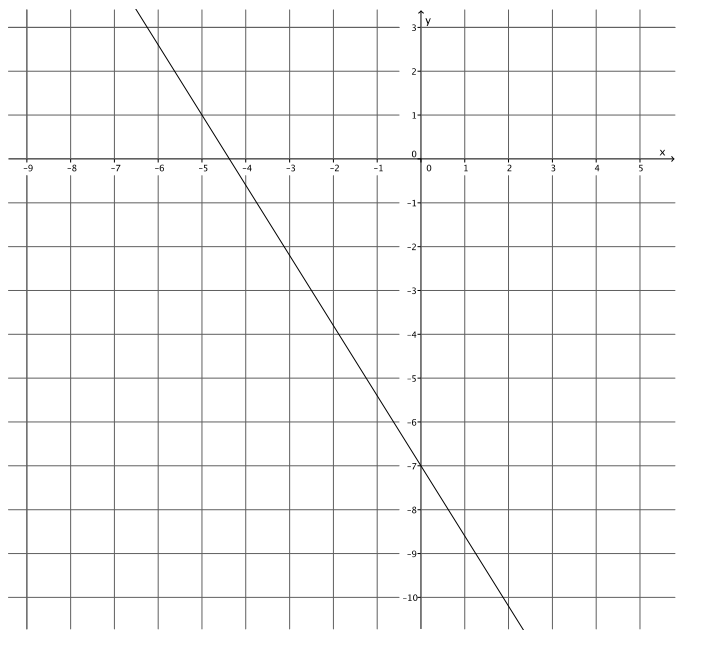
Answer:
y = – \(\frac{8}{5}\) x – 7
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = – \(\frac{8}{5}\) x – 7
(y = – \(\frac{8}{5}\) x – 7)5
5y = – 8x – 35
8x + 5y = – 8x + 8x – 35
8x + 5y = – 35
Eureka Math Grade 8 Module 4 Lesson 20 Problem Set Answer Key
Question 1.
Write the equation that represents the line shown.
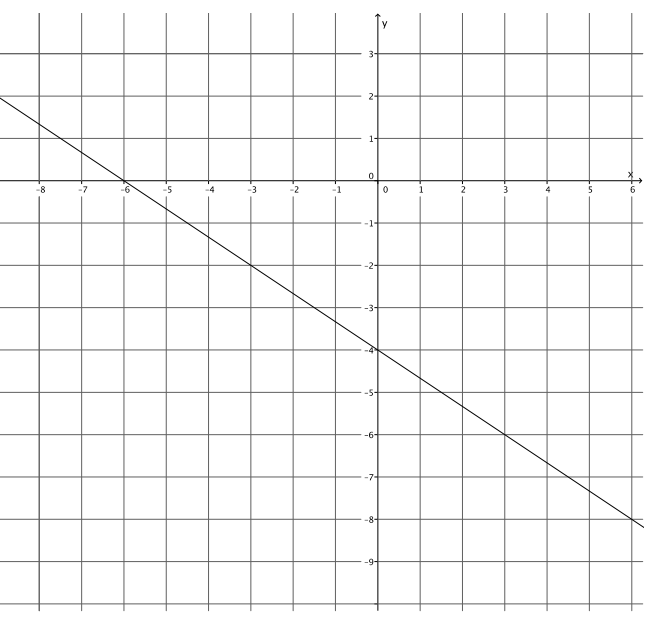
Answer:
y = – \(\frac{2}{3}\) x – 4
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = – \(\frac{2}{3}\) x – 4
(y = – \(\frac{2}{3}\) x – 4)3
3y = – 2x – 12
2x + 3y = – 2x + 2x – 12
2x + 3y = – 12
Question 2.
Write the equation that represents the line shown.
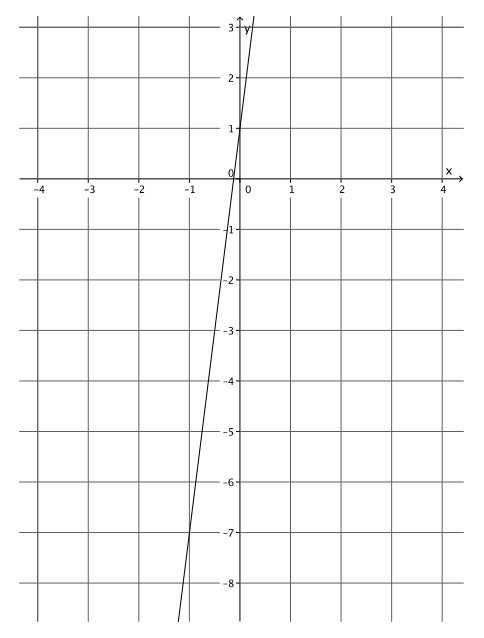
Answer:
y = 8x + 1
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = 8x + 1
– 8x + y = 8x – 8x + 1
– 8x + y = 1
– 1( – 8x + y = 1)
8x – y = – 1
Question 3.
Write the equation that represents the line shown.
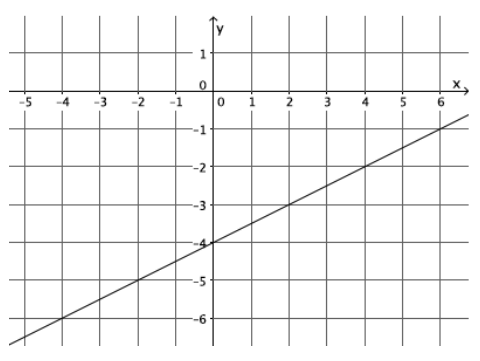
Answer:
y = \(\frac{1}{2}\) x – 4
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = \(\frac{1}{2}\) x – 4
(y = \(\frac{1}{2}\) x – 4)2
2y = x – 8
– x + 2y = x – x – 8
– x + 2y = – 8
– 1( – x + 2y = – 8)
x – 2y = 8
Question 4.
Write the equation that represents the line shown.
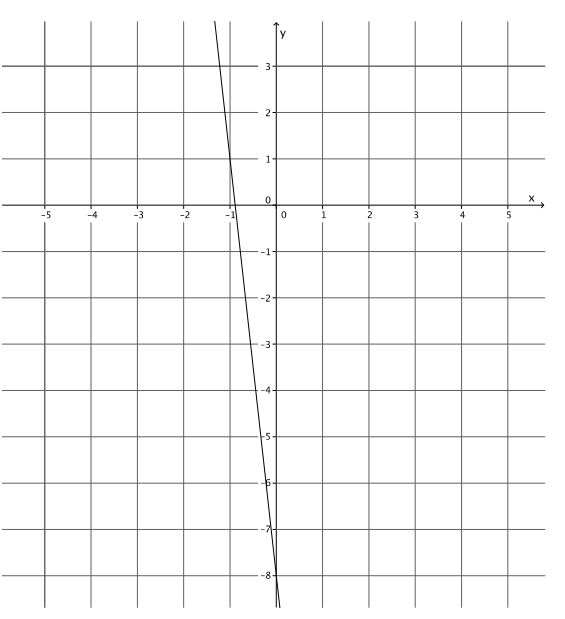
Answer:
y = – 9x – 8
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = – 9x – 8
9x + y = – 9x + 9x – 8
9x + y = – 8
Question 5.
Write the equation that represents the line shown.

Answer:
y = 2x – 14
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = 2x – 14
– 2x + y = 2x – 2x – 14
– 2x + y = – 14
– 1( – 2x + y = – 14)
2x – y = 14
Question 6.
Write the equation that represents the line shown.
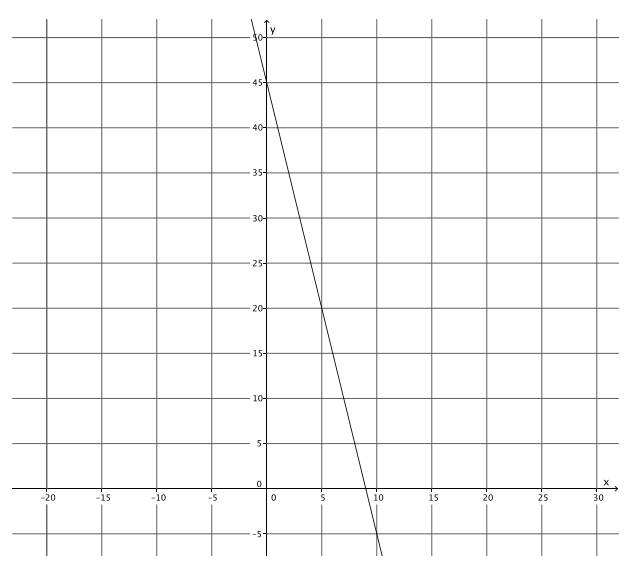
Answer:
y = – 5x + 45
Use the properties of equality to change the equation from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = – 5x + 45
5x + y = – 5x + 5x + 45
5x + y = 45
Eureka Math Grade 8 Module 4 Lesson 20 Exit Ticket Answer Key
Question 1.
Write an equation in slope – intercept form that represents the line shown.
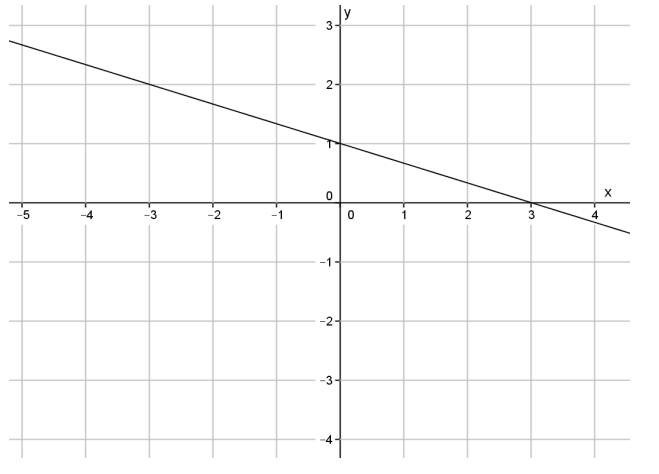
Answer:
y = – \(\frac{1}{3}\) x + 1
Question 2.
Use the properties of equality to change the equation you wrote for Problem 1 from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = – \(\frac{1}{3}\) x + 1
(y = – \(\frac{1}{3}\) x + 1)3
3y = – x + 3
x + 3y = – x + x + 3
x + 3y = 3
Question 3.
Write an equation in slope – intercept form that represents the line shown.
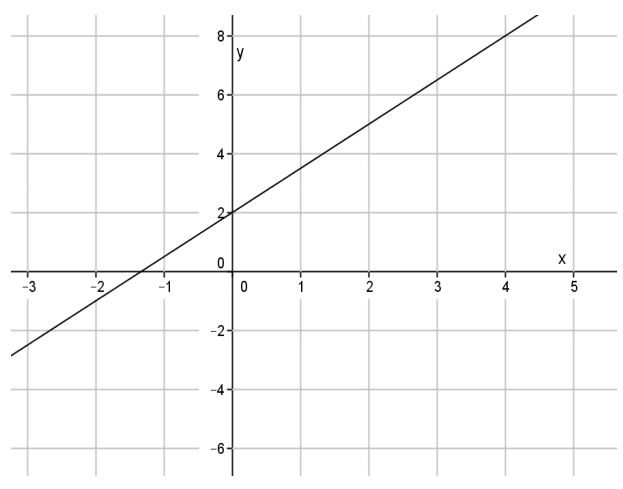
Answer:
y = \(\frac{3}{2}\) x + 2
Question 4.
Use the properties of equality to change the equation you wrote for Problem 3 from slope – intercept form, y = mx + b, to standard form, ax + by = c, where a, b, and c are integers, and a is not negative.
Answer:
y = \(\frac{3}{2}\) x + 2
(y = \(\frac{3}{2}\) x + 2)2
2y = 3x + 4
– 3x + 2y = 3x – 3x + 4
– 3x + 2y = 4
– 1( – 3x + 2y = 4)
3x – 2y = – 4