Engage NY Eureka Math 8th Grade Module 4 Lesson 18 Answer Key
Eureka Math Grade 8 Module 4 Lesson 19 Opening Exercise Answer Key
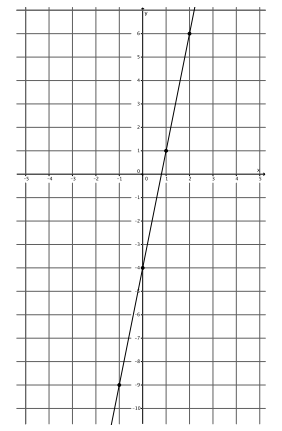
Examine each of the graphs and their equations. Identify the coordinates of the point where the line intersects the y-axis. Describe the relationship between the point and the equation y=mx+b.
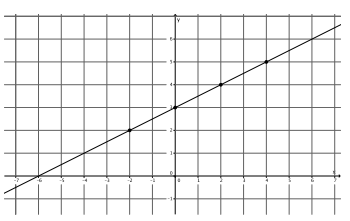
a. y=\(\frac{1}{2}\) x+3
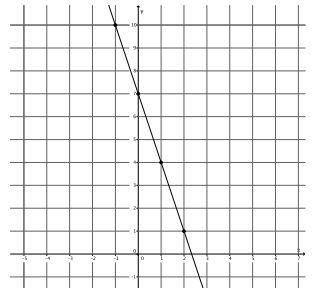
b. y=-3x+7
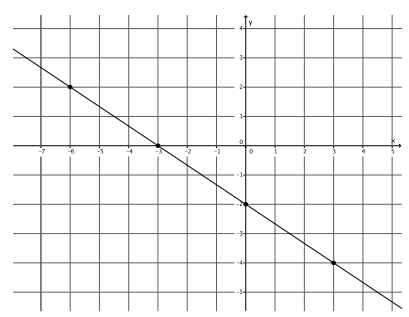
c. y=-\(\frac{2}{3}\) x-2
d. y=5x-4
Answer:
A point is noted in each graph above where the line intersects the y-axis:
y=\(\frac{1}{2}\) x+3, (0,3)
y=-3x+7, (0,7)
y=-\(\frac{2}{3}\) x-2, (0,-2)
y=5x-4, (0,-4)
In each equation, the number b was the y-coordinate of the point where the line intersected the y-axis.
Eureka Math Grade 8 Module 4 Lesson 19 Example Answer Key
Graph an equation in the form of y=mx+b.
Example 1.
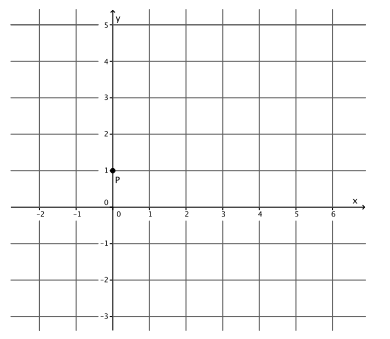
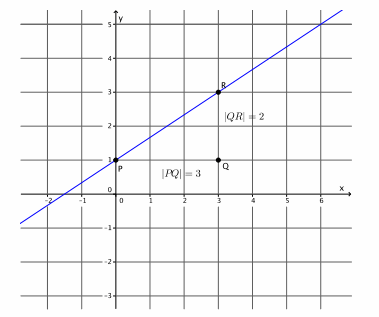
Graph the equation y=\(\frac{2}{3}\) x+1. Name the slope and y-intercept point.
Answer:
The slope is m=\(\frac{2}{3}\), and the y-intercept point is (0,1).
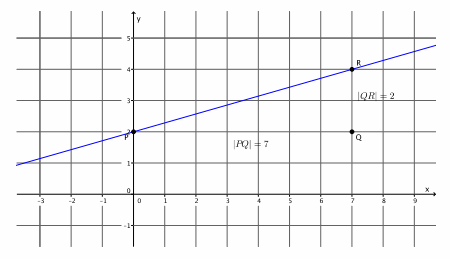
→ To graph the equation, we must begin with the known point. In this case, that is the y-intercept point. We cannot begin with the slope because the slope describes the rate of change between two points. That means we need a point to begin with. On a graph, we plot the point (0,1).
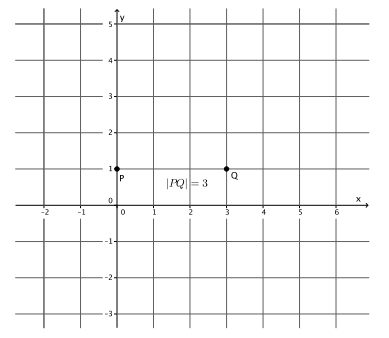
→ Next, we use the slope to find the second point. We know that m=\(\frac{|Q R|}{|P Q|}\) =\(\frac{2}{3}\). The slope tells us exactly how many units to go to the right of P to find point Q and then how many vertical units we need to go from Q to find point R. How many units will we go to the right in order to find point Q? How do you know?
→ We need to go 3 units to the right of point P to find Q. We go 3 units because |PQ|=3.
→ How many vertical units from point Q must we go to find point R? How do you know?
→ We need to go 2 units from point Q to find R. We go 2 units because |QR|=2.
→ Will we go up from point Q or down from point Q to find R? How do you know?
→ We need to go up because the slope is positive. That means that the line will be left-to-right inclining.
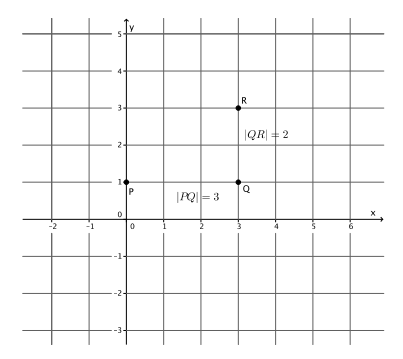
→ Since we know that the line joining two distinct points of the form y=mx+b has slope m, and we specifically constructed points P and R with the slope in mind, we can join the points with a line.
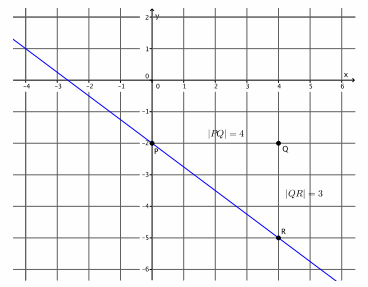
Example 2.
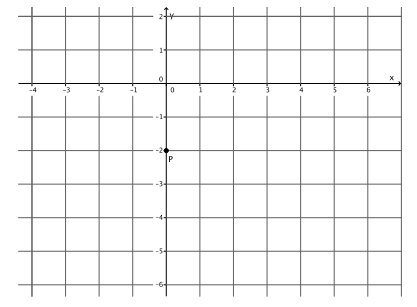
Graph the equation y=-\(\frac{3}{4}\) x-2. Name the slope and y-intercept point.
Answer:
The slope is m=-\(\frac{3}{4}\), and the y-intercept point is (0,-2).
→ How do we begin?
→ We must begin by putting a known point on the graph, (0,-2).
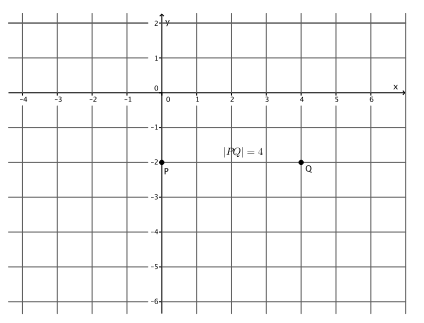
→ We know that m=\(\frac{|Q R|}{|P Q|}\) =-\(\frac{3}{4}\). How many units will we go to the right in order to find point Q? How do you know?
→ We need to go 4 units to the right of point P to find Q. We go 4 units because |PQ|=4.
→ How many units from point Q must we go to find point R? How do you know?
→ We need to go 3 units from point Q to find R. We go 3 units because |QR|=3.
→ Will we go up from point Q or down from point Q to find R? How do you know?
→ We need to go down from point Q to point R because the slope is negative. That means that the line will be left-to-right declining.
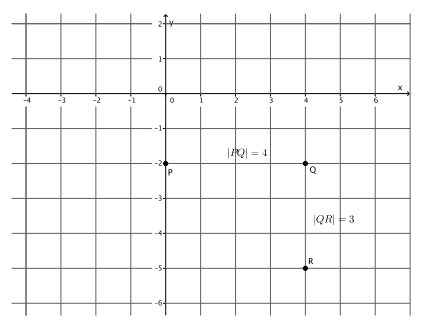
→ Now we draw the line through the points P and R.
Example 3
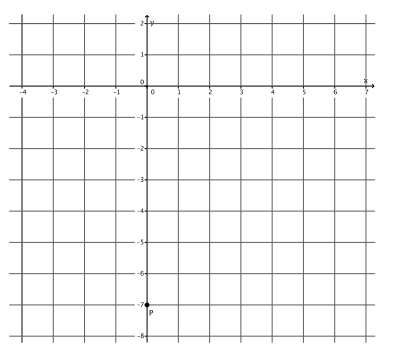
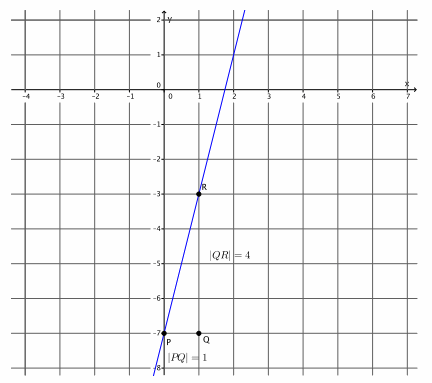
Graph the equation y=4x-7. Name the slope and y-intercept point.
Answer:
The slope is m=4, and the y-intercept point is (0,-7).
→ Graph the equation y=4x-7. Name the slope and y-intercept point.
→ The slope is m=4, and the y-intercept point is (0,-7).
→ How do we begin?
→ We must begin by putting a known point on the graph, (0,-7).
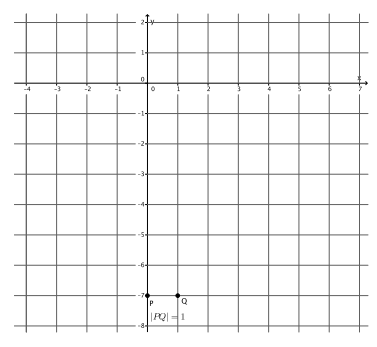
→ Notice this time that the slope is the integer 4. In the last two examples, our slopes have been in the form of a fraction so that we can use the information in the numerator and denominator to determine the lengths of |PQ| and |QR|. Since m=\(\frac{|Q R|}{|P Q|}\) =4, what fraction can we use to represent slope to help us graph?
→ The number 4 is equivalent to the fraction \(\frac{4}{1}\).
→ Using m=\(\frac{|Q R|}{|P Q|}\) =\(\frac{4}{1}\), how many units will we go to the right in order to find point Q? How do you know?
→ We need to go 1 unit to the right of point P to find Q. We go 1 unit because |PQ|=1.
→ How many vertical units from point Q must we go to find point R? How do you know?
→ We need to go 4 units from point Q to find R. We go 4 units because |QR|=4.
→ Will we go up from point Q or down from point Q to find R? How do you know?
→ We need to go up from point Q to point R because the slope is positive. That means that the line will be left-to-right inclining.
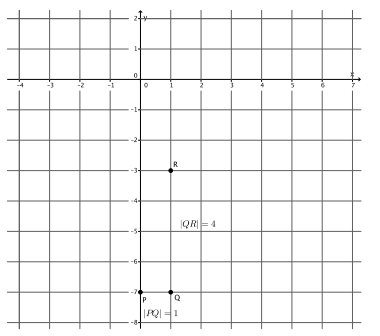
→ Now we join the points P and R to make the line.
Eureka Math Grade 8 Module 4 Lesson 19 Exercise Answer Key
Exercises 1–4 (5 minutes)
Students complete Exercises 1–4 individually or in pairs.
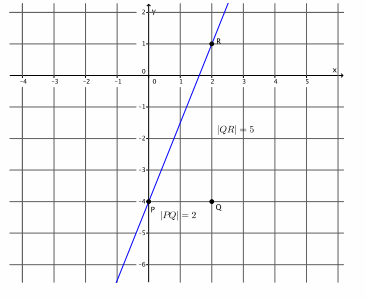
Exercise 1.
Graph the equation y=\(\frac{5}{2}\) x -4.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=\(\frac{5}{2}\), and the y-intercept point is (0,-4).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
Exercise 2.
Graph the equation y=-3x+6.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=-3, and the y-intercept point is (0,6).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
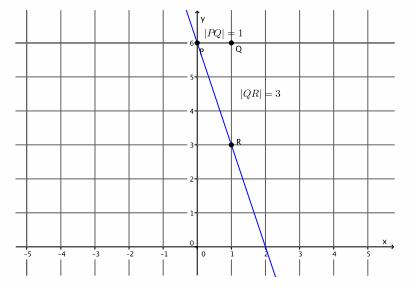
Question 3.
The equation y=1x+0 can be simplified to y=x. Graph the equation y=x.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=1, and the y-intercept point is (0,0).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
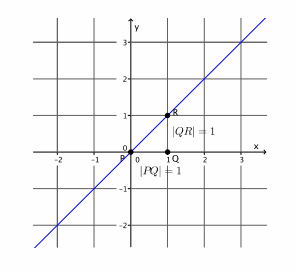
Question 4.
Graph the point (0,2).
Answer:
a. Find another point on the graph using the slope, m=\(\frac{2}{7}\).
b. Connect the points to make the line.
c. Draw a different line that goes through the point (0,2) with slope m=\(\frac{2}{7}\). What do you notice?
Answer:
Only one line can be drawn through the given point with the given slope.
Exercises 5–6
Students complete Exercises 5–6 individually or in pairs.
Exercise 5.
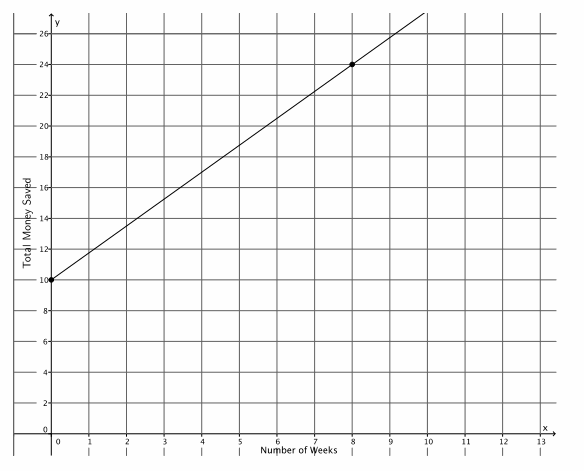
A bank put $10 into a savings account when you opened the account. Eight weeks later, you have a total of $24. Assume you saved the same amount every week.
a. If y is the total amount of money in the savings account and x represents the number of weeks, write an equation in the form y=mx+b that describes the situation.
Answer:
24=m(8)+10
14=8m
\(\frac{14}{8}\)=m
\(\frac{7}{4}\)=m
y=\(\frac{7}{4}\) x+10
b. Identify the slope and the y-intercept point. What do these numbers represent?
Answer:
The slope is \(\frac{7}{4}\), and the y-intercept point is (0,10). The y-intercept point represents the amount of money the bank gave me, in the amount of $10. The slope represents the amount of money I save each week, \(\frac{7}{4}\)=$1.75.
c. Graph the equation on a coordinate plane.
Answer:
d. Could any other line represent this situation? For example, could a line through point (0,10) with slope \(\frac{7}{5}\) represent the amount of money you save each week? Explain.
Answer:
No, a line through point (0,10) with slope \(\frac{7}{5}\) cannot represent this situation. That line would show that at the end of the 8 weeks I would have $21.20, but I was told that I would have $24 by the end of the 8 weeks.
Exercise 6.
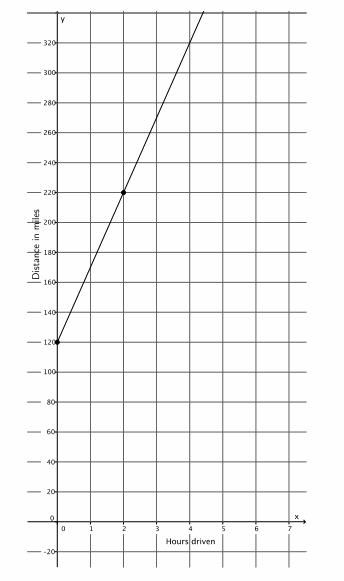
A group of friends are on a road trip. After 120 miles, they stop to eat lunch. They continue their trip and drive at a constant rate of 50 miles per hour.
a. Let y represent the total distance traveled, and let x represent the number of hours driven after lunch. Write an equation to represent the total number of miles driven that day.
Answer:
y=50x+120
b. Identify the slope and the y-intercept point. What do these numbers represent?
Answer:
The slope is 50 and represents the rate of driving. The y-intercept point is 120 and represents the number of miles they had already driven before driving at the given constant rate.
c. Graph the equation on a coordinate plane.
Answer:
d. Could any other line represent this situation? For example, could a line through point (0,120) with slope 75 represent the total distance the friends drive? Explain.
Answer:
No, a line through point (0,120) with a slope of 75 could not represent this situation. That line would show that after an hour, the friends traveled a total distance of 195 miles. According to the information given, the friends would only have traveled 170 miles after one hour.
Eureka Math Grade 8 Module 4 Lesson 19 Exit Ticket Answer Key
Mrs. Hodson said that the graphs of the equations below are incorrect. Find the student’s errors, and correctly graph the equations.
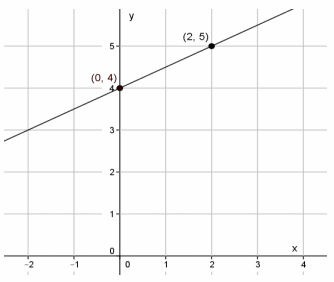
Question 1.
Student graph of the equation y=\(\frac{1}{2}\) x+4:
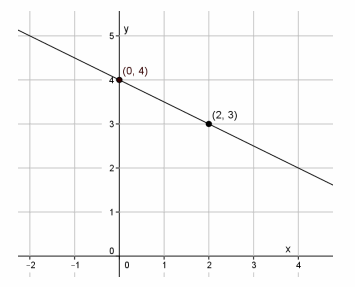
Error:
Answer:
The student should have gone up 1 unit when finding |QR| since the slope is positive.
Correct graph of the equation:
Answer:
Question 2.
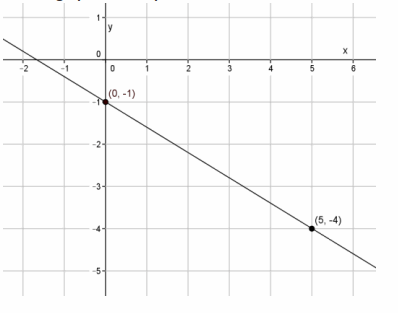
Student graph of the equation y=-\(\frac{3}{5}\) x-1:
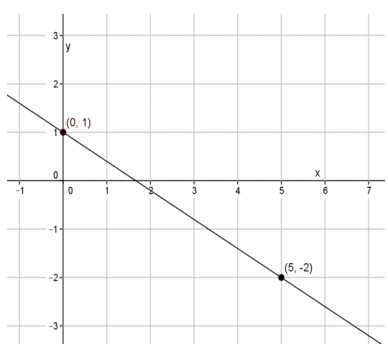
Error:
Answer:
The student did not find the y-intercept point correctly. It should be the point (0,-1).
Correct graph of the equation:
Answer:
Eureka Math Grade 8 Module 4 Lesson 19 Problem Set Answer Key
Students practice graphing equations using y-intercept point and slope. Students need graph paper to complete the Problem Set. Optional Problem 11 has students show that there is only one line passing through a point with a given negative slope.
Graph each equation on a separate pair of x- and y-axes.
Question 1.
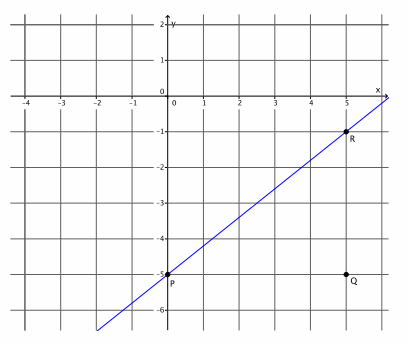
Graph the equation y=\(\frac{4}{5}\) x-5.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=\(\frac{4}{5}\), and the y-intercept point is (0,-5).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
Question 2.
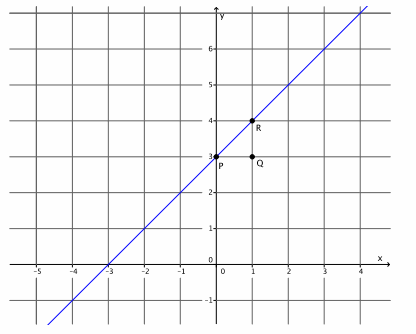
Graph the equation y=x+3.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=1, and the y-intercept point is (0,3).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
Question 3.
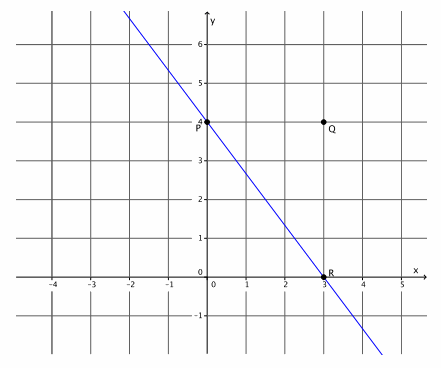
Graph the equation y=-\(\frac{4}{3}\) x+4.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=-\(\frac{4}{3}\), and the y-intercept point is (0,4).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
Question 4.
Graph the equation y=\(\frac{5}{2}\) x.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=\(\frac{5}{2}\), and the y-intercept point is (0,0).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
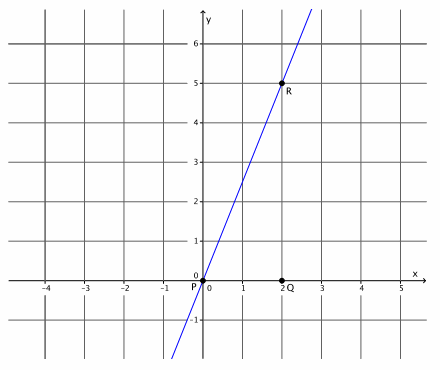
Question 5.
Graph the equation y=2x-6.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=2, and the y-intercept point is (0,-6).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
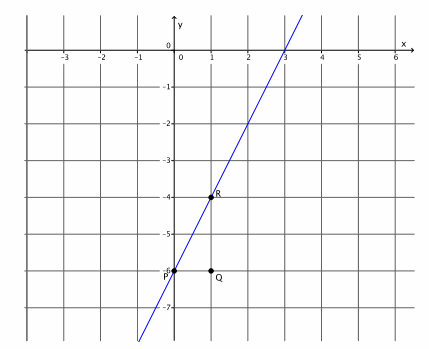
Question 6.
Graph the equation y=-5x+9.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=-5, and the y-intercept point is (0,9).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
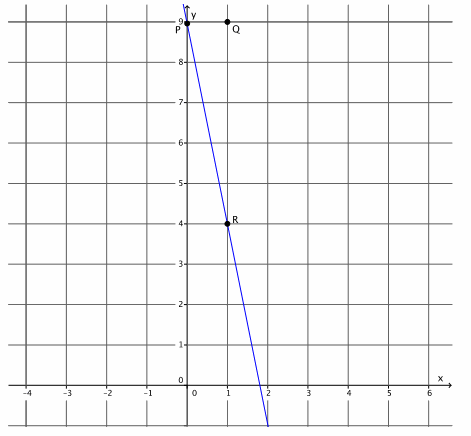
Question 7.
Graph the equation y=\(\frac{1}{3}\) x+1.
a. Name the slope and the y-intercept point.
Answer:
The slope is m=\(\frac{1}{3}\), and the y-intercept point is (0,1).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
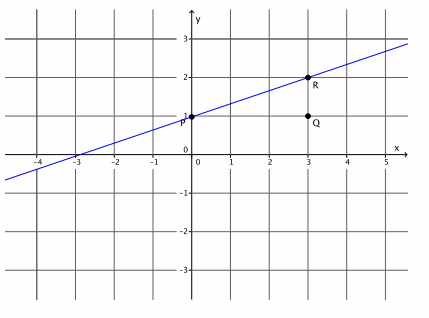
Question 8.
Graph the equation 5x+4y=8. (Hint: Transform the equation so that it is of the form y=mx+b.)
a. Name the slope and the y-intercept point.
Answer:
5x+4y=8
5x-5x+4y=8-5x
4y=8-5x
\(\frac{4}{4}\) y=\(\frac{8}{4}\)–\(\frac{5}{4}\) x
y=2-\(\frac{5}{4}\) x
y=-\(\frac{5}{4}\) x+2
The slope is m=-\(\frac{5}{4}\), and the y-intercept point is (0,2).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
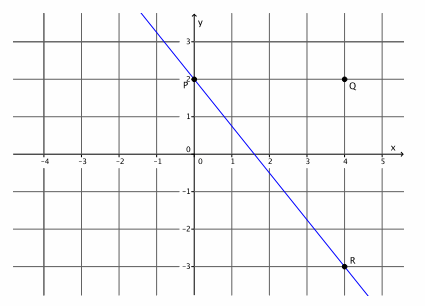
Question 9.
Graph the equation -2x+5y=30.
a. Name the slope and the y-intercept point.
Answer:
-2x+5y=30
2x+2x+5y=30+2x
5y=30+2x
\(\frac{5}{5}\) y=\(\frac{30}{5}\)+\(\frac{2}{5}\) x
y=6+\(\frac{2}{5}\) x
y=\(\frac{2}{5}\) x+6
The slope is m=\(\frac{2}{5}\), and the y-intercept point is (0,6).
b. Graph the known point, and then use the slope to find a second point before drawing the line.
Answer:
Question 10.
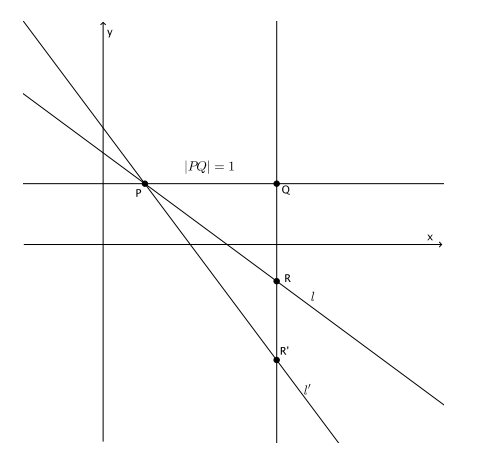
Let l and l’ be two lines with the same slope m passing through the same point P. Show that there is only one line with a slope m, where m<0, passing through the given point P. Draw a diagram if needed.
Answer:
First, assume that there are two different lines l and l’ with the same negative slope passing through P. From point P, I mark a point Q one unit to the right. Then, I draw a line parallel to the y-axis through point Q. The intersection of this line and line l and l’ are noted with points R and R’, respectively. By definition of slope, the lengths |QR| and |QR’ | represent the slopes of lines l and l’, respectively. We are given that the lines have the same slope, which means that lengths |QR| and |QR’| are equal. Since that is true, then points R and R’coincide and so do lines l and l’. Therefore, our assumption that they are different lines is false; l and l’ must be the same line. Therefore, there is only one line with slope m passing through the given point P.