Engage NY Eureka Math 8th Grade Module 4 Lesson 16 Answer Key
Eureka Math Grade 8 Module 4 Lesson 16 Example Answer Key
Example 1.
Using what you learned in the last lesson, determine the slope of the line with the following graph.
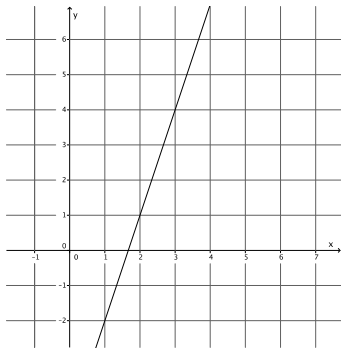
Answer:
The slope of the line is 3.
Example 2.
Using what you learned in the last lesson, determine the slope of the line with the following graph.
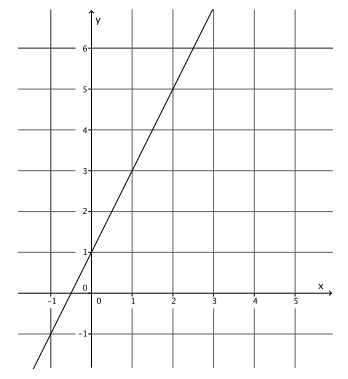
Answer:
The slope of this line is 2.
Example 3.
What is different about this line compared to the last two examples?
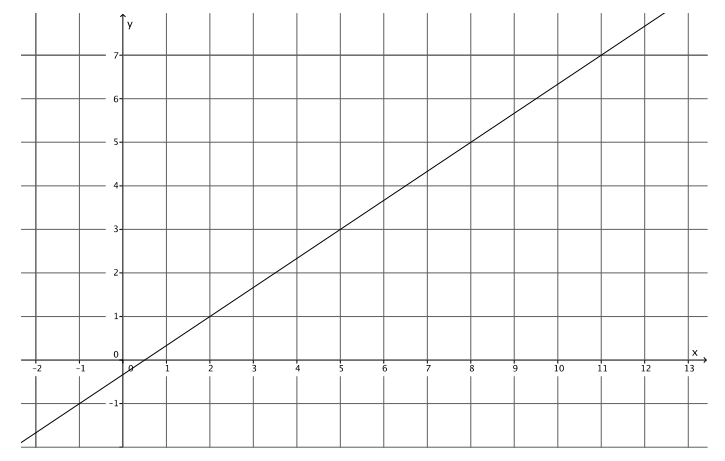
Answer:
This time, if we choose two points on the line that have a horizontal distance at 1, we cannot precisely determine the slope of the line because the vertical change is not an integer. It is some fractional amount.
→ Make a conjecture about how you could find the slope of this line.
Have students write their conjectures and share their ideas about how to find the slope of the line in this example; then, continue with the Discussion that follows.
Eureka Math Grade 8 Module 4 Lesson 16 Exercise Answer Key
Exercise
Let’s investigate concretely to see if the claim that we can find slope between any two points is true.
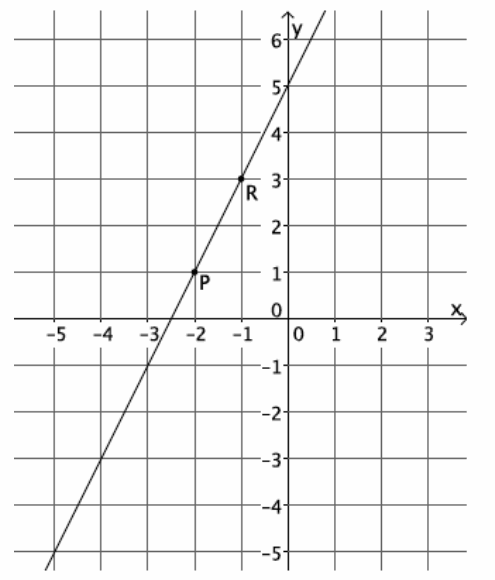
a. Select any two points on the line to label as P and R.
Answer:
Sample points are selected on the graph.
b. Identify the coordinates of points P and R.
Answer:
Sample points are labeled on the graph.
c. Find the slope of the line using as many different points as you can. Identify your points, and show your work below.
Answer:
Points selected by students will vary, but the slope should always equal 2. Students could choose to use points (0,5), (-1,3), (-2,1), (-3,-1), (-4,-3), and (-5,-5).
Eureka Math Grade 8 Module 4 Lesson 16 Problem Set Answer Key
Students practice finding slope between any two points on a line. Students also see that m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\) yields the same result as m=\(\frac{r_{2}-p_{2}}{r_{1}-p_{1}}\).
Question 1.
Calculate the slope of the line using two different pairs of points.
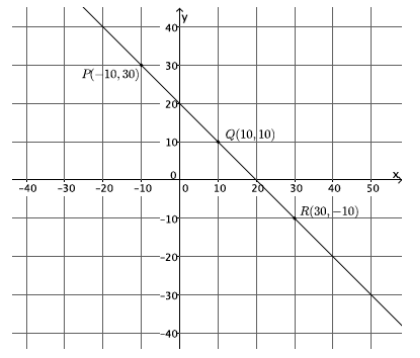
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{30-(-10)}{-10-30}\)
=\(\frac{40}{-40}\)
=\(\frac{1}{1}\)
=-1
m=\(\frac{q_{2}-r_{2}}{q_{1}-r_{1}}\)
=\(\frac{10-(-10)}{10-30}\)
=\(\frac{20}{-20}\)
=-1
Question 2.
Calculate the slope of the line using two different pairs of points.
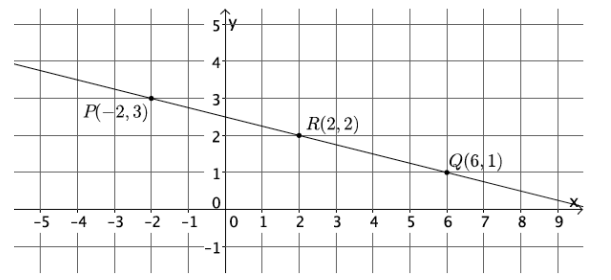
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{3-2}{-2-2}\)
=\(\frac{1}{-4}\)
=-\(\frac{1}{4}\)
m=\(\frac{q_{2}-r_{2}}{q_{1}-r_{1}}\)
=\(\frac{1-2}{6-2}\)
=\(\frac{-1}{4}\)
=-\(\frac{1}{4}\)
Question 3.
Calculate the slope of the line using two different pairs of points.
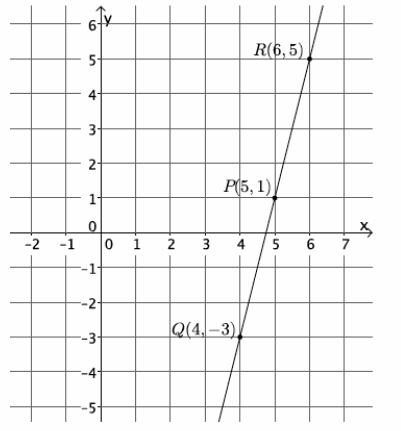
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{1-5}{5-6}\)
=\(\frac{-4}{-1}\)
=\(\frac{4}{1}\)
=4
m=\(\frac{q_{2}-r_{2}}{q_{1}-r_{1}}\)
=\(\frac{-3-5}{4-6}\)
=\(\frac{-8}{-2}\)
=4
Question 4.
Calculate the slope of the line using two different pairs of points.
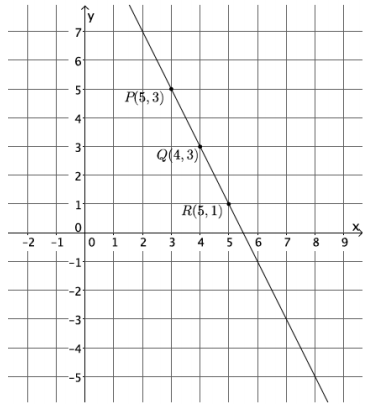
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{5-1}{3-5}\)
=\(\frac{4}{-2}\)
=\(-\frac{2}{1}\)
=-2
m=\(\frac{q_{2}-r_{2}}{q_{1}-r_{1}}\)
=\(\frac{3-1}{4-5}\)
=\(\frac{2}{-1}\)
=-2
Question 5.
Calculate the slope of the line using two different pairs of points.
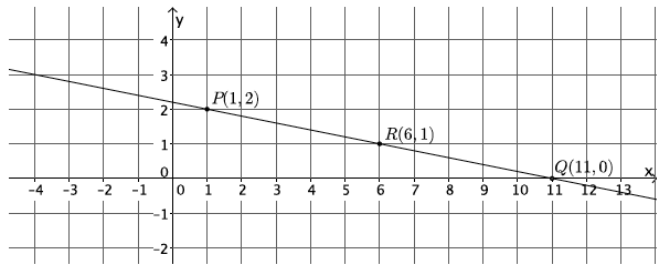
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{2-1}{1-6}\)
=\(\frac{1}{-5}\)
=-\(\frac{1}{5}\)
m=\(\frac{q_{2}-r_{2}}{q_{1}-r_{1}}\)
=\(\frac{0-1}{11-6}\)
=\(\frac{-1}{5}\)
=-\(\frac{1}{5}\)
Question 6.
Calculate the slope of the line using two different pairs of points.
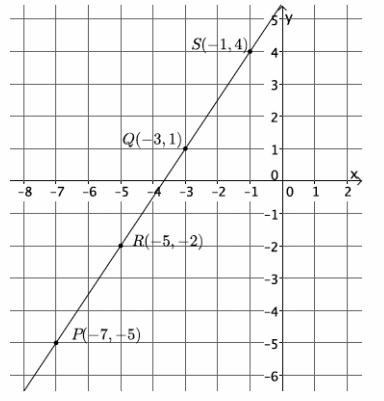
a. Select any two points on the line to compute the slope.
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{-5-(-2)}{-7-(-5)}\)
=\(\frac{-3}{-2}\)
=\(\frac{3}{2}\)
b. Select two different points on the line to calculate the slope.
Answer:
Let the two new points be (-3,1) and (-1,4).
m=\(\frac{q_{2}-s_{2}}{q_{1}-s_{1}}\)
=\(\frac{1-4}{-3-(-1)}\)
=\(\frac{-3}{-2}\)
=\(\frac{3}{2}\)
c. What do you notice about your answers in parts (a) and (b)? Explain.
Answer:
The slopes are equal in parts (a) and (b). This is true because of what we know about similar triangles.
The slope triangle that is drawn between the two points selected in part (a) is similar to the slope triangle that is drawn between the two points in part (b) by the AA criterion. Then, because the corresponding sides of similar triangles are equal in ratio, the slopes are equal.
Question 7.
Calculate the slope of the line in the graph below.
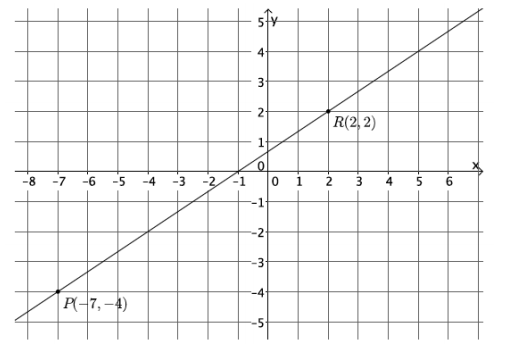
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{-4-2}{-7-2}\)
=\(\frac{-6}{-9}\)
=\(\frac{2}{3}\)
Question 8.
Your teacher tells you that a line goes through the points (-6, \(\frac{1}{2}\)) and (-4,3).
a. Calculate the slope of this line.
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{\frac{1}{2}-3}{-6-(-4)}\)
=\(\frac{-\frac{5}{2}}{-2}\)
= \(\frac{\frac{5}{2}}{2}\)
=\(\frac{5}{2}\)÷2
=\(\frac{5}{2}\)×\(\frac{1}{2}\)
= \(\frac{5}{4}\)
b. Do you think the slope will be the same if the order of the points is reversed? Verify by calculating the slope, and explain your result.
The slope should be the same because we are joining the same two points.
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
= \(\frac{3-\frac{1}{2}}{-4-(-6)}\)
= \(\frac{\frac{5}{2}}{2}\)
= \(\frac{5}{4}\)
Since the slope of a line can be computed using any two points on the same line, it makes sense that it does not matter which point we name as P and which point we name as R.
Question 9.
Use the graph to complete parts (a)–(c).
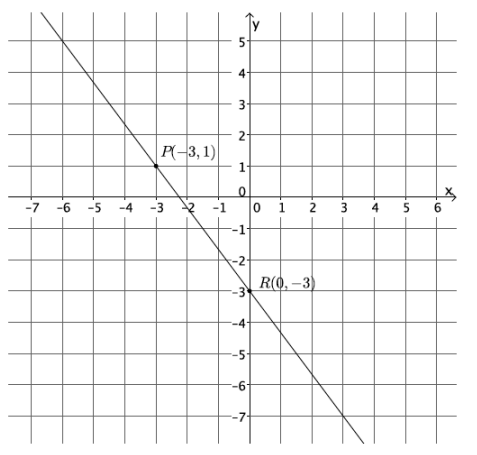
a. Select any two points on the line to calculate the slope.
Answer:
m=\(\frac{p_{2}-r_{2}}{p_{1}-r_{1}}\)
=\(\frac{1-(-3)}{-3-0}\)
=\(\frac{4}{-3}\)
=-\(\frac{4}{3}\)
b. Compute the slope again, this time reversing the order of the coordinates.
Answer:
m=\(\frac{\left(r_{2}-p_{2}\right)}{\left(r_{1}-p_{1}\right)}\)
=\(\frac{-3-1}{0-(-3)}\)
=\(\frac{-4}{3}\)
=-\(\frac{4}{3}\)
c. What do you notice about the slopes you computed in parts (a) and (b)?
Answer:
The slopes are equal.
d. Why do you think m=\(\frac{\left(p_{2}-r_{2}\right)}{\left(p_{1}-r_{1}\right)}\)=\(\frac{\left(r_{2}-p_{2}\right)}{\left(r_{1}-p_{1}\right)}\).?
Answer:
If I multiply the first fraction by \(\frac{-1}{-1}\), then I get the second fraction:
\(\frac{-1}{-1}\)×\(\left(\frac{\left(p_{2}-r_{2}\right)}{\left(p_{1}-r_{1}\right)}\right)\)=\(\frac{\left(r_{2}-p_{2}\right)}{\left(r_{1}-p_{1}\right)}\).
I can do the same thing to the second fraction to obtain the first:
\(\frac{-1}{-1}\)×\(\left(\frac{\left(r_{2}-p_{2}\right)}{\left(r_{1}-p_{1}\right)}\right)\)=\(\frac{\left(p_{2}-r_{2}\right)}{\left(p_{1}-r_{1}\right)}\)
Also, since I know that I can find the slope between any two points, it should not matter which point I pick first.
Question 10.
Each of the lines in the lesson was non-vertical. Consider the slope of a vertical line, x=2. Select two points on the line to calculate slope. Based on your answer, why do you think the topic of slope focuses only on non-vertical lines?
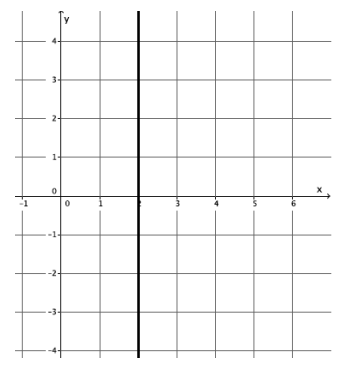
Answer:
Students can use any points on the line x=2 to determine that the slope is undefined. The computation of slope using the formula leads to a fraction with zero as its denominator. Since the slope of a vertical line is undefined, there is no need to focus on them.
Challenge:
Question 11.
A certain line has a slope of \(\frac{1}{2}\). Name two points that may be on the line.
Answer:
Answers will vary. Accept any answers that have a difference in y-values equal to 1 and a difference of x-values equal to 2. Points (6,4) and (4,3) may be on the line, for example.
Eureka Math Grade 8 Module 4 Lesson 16 Exit Ticket Answer Key
Find the rate of change of the line by completing parts (a) and (b).
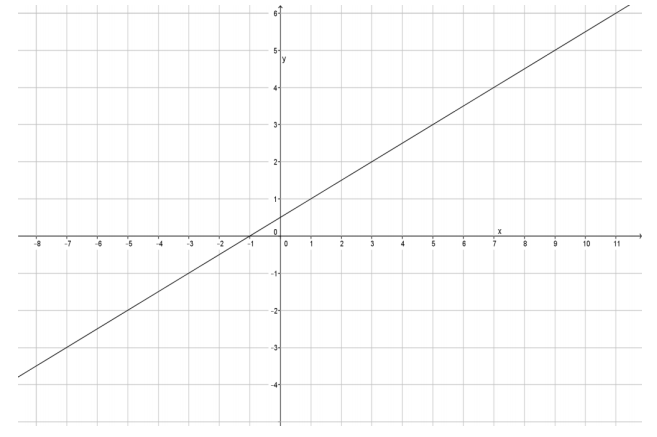
a. Select any two points on the line to label as P and R. Name their coordinates.
Answer:
Answers will vary. Other points on the graph may have been chosen.
P(-1,0) and R(5,3)
b. Compute the rate of change of the line.
Answer:
m = \(\frac{\left(p_{2}-r_{2}\right)}{\left(p_{1}-r_{1}\right)}\)
m=\(\frac{0-3}{-1-5}\)
=\(\frac{-3}{-6}\)
=\(\frac{1}{2}\)