Eureka Math Grade 8 Module 3 Lesson 3 Answer Key

Engage NY Eureka Math 8th Grade Module 3 Lesson 3 Answer Key

Eureka Math Grade 8 Module 3 Lesson 3 Example Answer Key

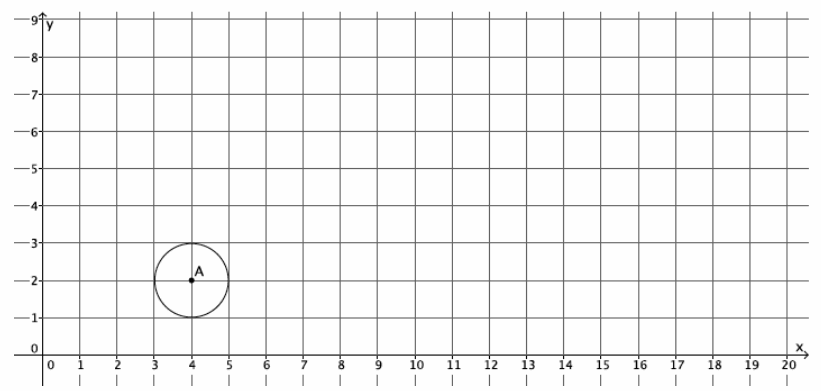
Example 1.
Dilate circle A from center O at the origin by scale factor r=3.

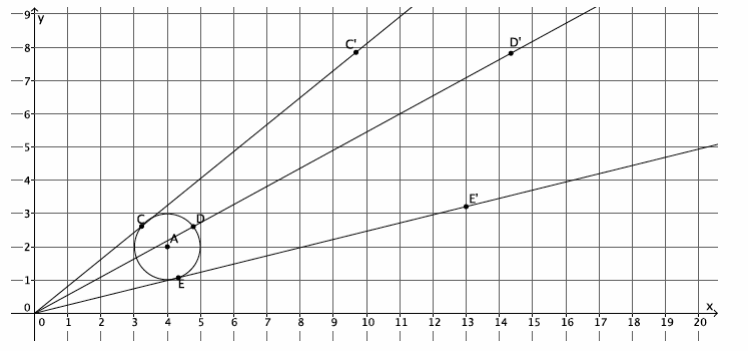
→ Are three points enough? Let’s try.
(Show a picture of three dilated points.) If we connect these three dilated points, what image do we get?
→ With just three points, the image looks like a triangle.

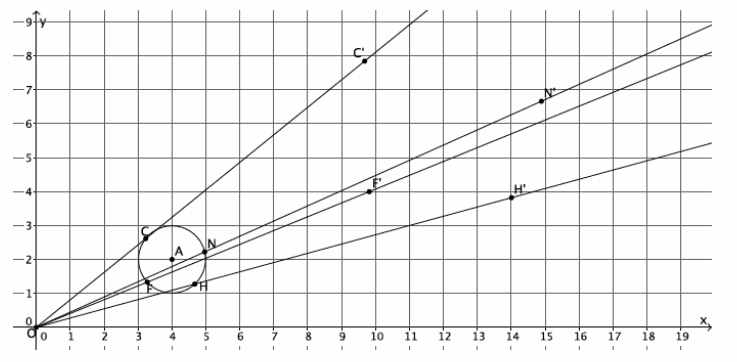
→ What if we dilate a fourth point? Is that enough? Let’s try.
→ (Show the picture of four dilated points.) If we connect these four dilated points, what image do we get?
→ With four points, the image looks like a quadrilateral.

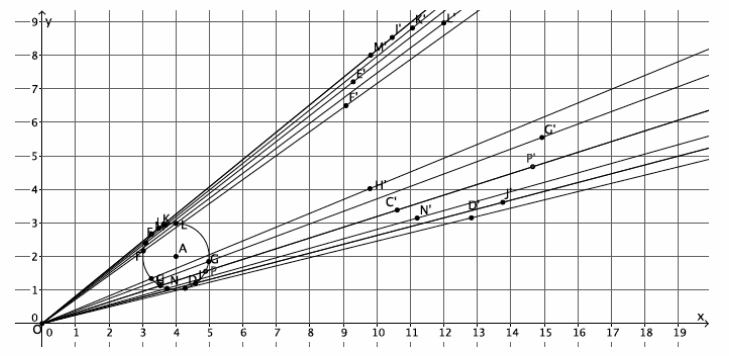
→ What if we dilate five, six, or ten points? What do you think?
→ The more points that are dilated, the more the image looks like a circle.
→ (Show the picture with many dilated points.)

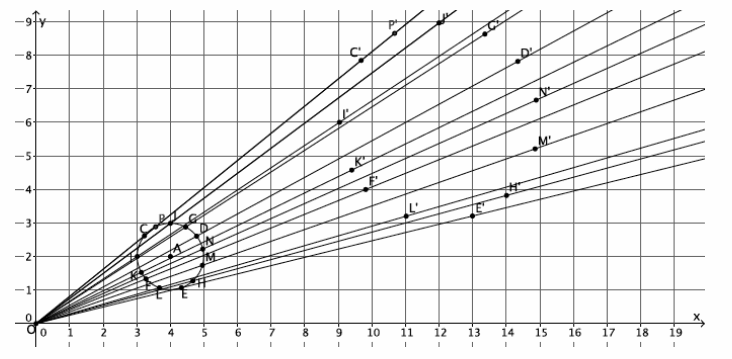
→ Notice that the shape of the dilated image is now unmistakably a circle. Dilations map circles to circles, so it is important that when we dilate a circle we choose our points carefully.
→ Would we have an image that looked like a circle if all of the points we considered were located on just one part of the circle? For example, what if all of our points were located on just the top half of the circle? Would the dilated points produce an image of the circle?

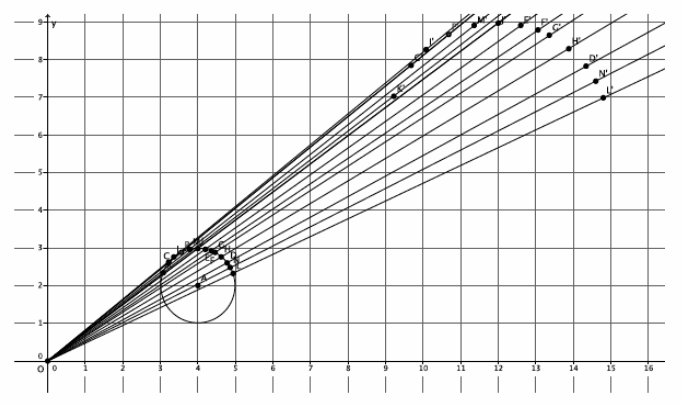
→ Or consider the image when we select points just on the lower half of the circle:

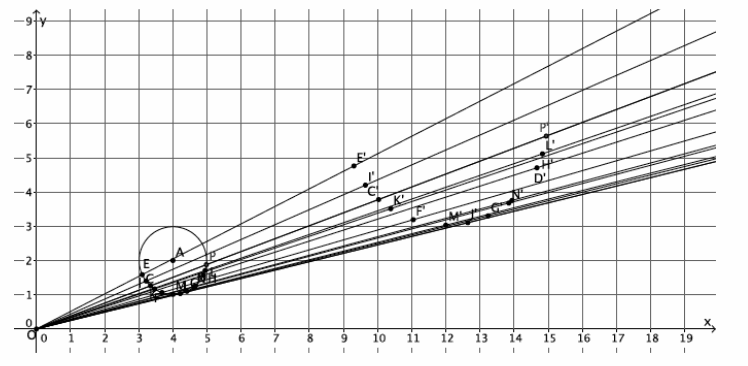
→ Consider the image when the points are focused on just the sides of the circle:

→ The images are not good enough to truly show that the original figure was a circle.
→ How should we select points to dilate when we have a curved figure?
→ We should select points on all parts of the curve, not just those points focused in one area.
→ The number of points to dilate that is enough is as many as are needed to produce a dilated image that looks like the original. For curved figures, like this circle, the more points you dilate the better. The location of the points you choose to dilate is also important. The points selected to dilate should be spread out evenly on the curve.

Example 2.
In the picture below, we have triangle ABC, that has been dilated from center O, by a scale factor of r=\(\frac{1}{3}\). It is noted by A’B’C’.

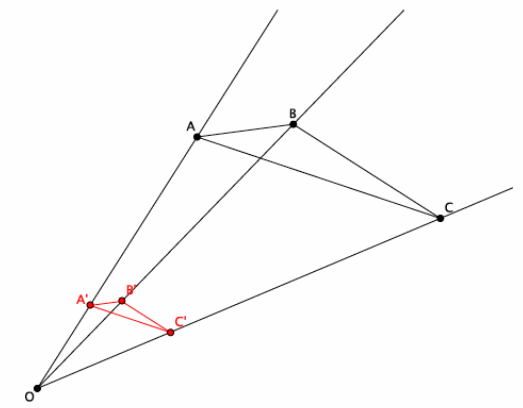
Ask students what can be done to map this new triangle, triangle A’B’C’, back to the original. Tell them to be as specific as possible. Students should write their conjectures or share with a partner.
→ Let’s use the definition of dilation and some side lengths to help us figure out how to map triangle A’B’C’ back onto triangle ABC. How are the lengths |OA’ | and |OA| related?
→ We know by the definition of dilation that |OA’|=r|OA|.
We know that r=\(\frac{1}{3}\). Let’s say that the length of segment OA is 6 units (we can pick any number, but 6 makes it easy for us to compute). What is the length of segment OA’?
→ Since |OA’|=\(\frac{1}{3}\) |OA|, and we are saying that the length of segment OA is 6, then |OA’|=\(\frac{1}{3}\)∙=2, and |OA’|=2 units.
→ Now, since we want to dilate triangle A’B’C’ to the size of triangle ABC, we need to know what scale factor r is required so that |OA|=r|OA’|. What scale factor should we use, and why?
→ We need a scale factor r=3 because we want |OA|=r|OA’|. Using the lengths from before, we have 6=r⋅2. Therefore, r=3.
→ Now that we know the scale factor, what precise dilation would map triangle A’B’C’ onto triangle ABC?
→ A dilation from center O with scale factor r=3

Example 3.
In the picture below, we have triangle DEF that has been dilated from center O by a scale factor of r=4. It is
noted by D’E’F’.

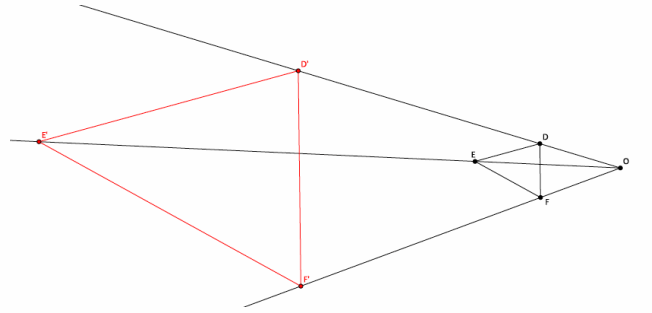
→ Based on the example we just did, make a conjecture about how we could map this new triangle D’E’F’ back onto the original triangle.
Let students attempt to prove their conjectures on their own or with a partner. If necessary, use the scaffolding questions that follow.
→ What is the difference between this problem and the last?
→ This time the scale factor is greater than one, so we need to shrink triangle D’E’F’ to the size of triangle DEF.
→ We know that r=4. Let’s say that the length of segment OF is 3 units. What is the length of segment OF’?
→ Since |OF’|=r|OF| and we are saying that the length of segment OF is 3, then |OF’|=4⋅3=12, and |OF’|=12 units.
→ Now, since we want to dilate triangle D’E’F’ to the size of triangle DEF, we need to know what scale factor r is required so that |OF|=r|OF’|. What scale factor should we use, and why?
→ We need a scale factor r=\(\frac{1}{4}\) because we want |OF|=r|OF’|. Using the lengths from before, we have 3=r⋅12. Therefore, r=\(\frac{1}{4}\).
→ What precise dilation would make triangle D’E’F’ the same size as triangle DEF?
→ A dilation from center O with scale factor r=\(\frac{1}{4}\) would make triangle D’E’F’ the same size as triangle DEF.

Eureka Math Grade 8 Module 3 Lesson 3 Exercise Answer Key

Exercises 1–2.

Exercise 1.
Dilate ellipse E, from center O at the origin of the graph, with scale factor r=2. Use as many points as necessary to develop the dilated image of ellipse E.
Answer:
The dilated image of E is shown in red below. Verify that students have dilated enough points evenly placed to get an image that resembles an ellipse.

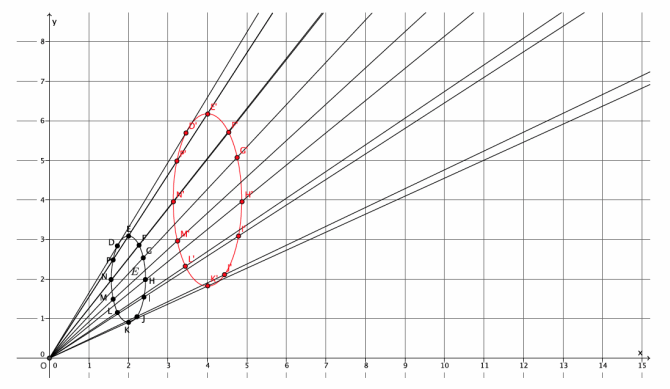
Exercise 2.
What shape was the dilated image?
Answer:
The dilated image was an ellipse. Dilations map ellipses to ellipses.

Exercise 3.
Triangle ABC has been dilated from center O by a scale factor of r=\(\frac{1}{4}\) denoted by triangle A’B’C’. Using a centimeter ruler, verify that it would take a scale factor of r=4 from center O to map triangle A’B’C’ onto triangle ABC.

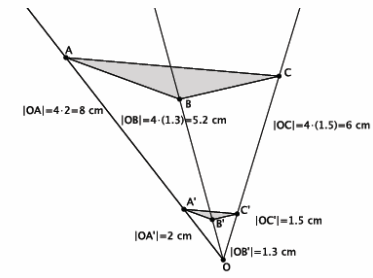
Answer:
Sample measurements provided. Note that, due to print variations, the measurements may be slightly different.
Verify that students have measured the lengths of segments from center O to each of the dilated points. Then, verify that students have multiplied each of the lengths by 4 to see that it really is the length of the segments from center O to the original points.

Eureka Math Grade 8 Module 3 Lesson 3 Problem Set Answer Key

Students practice dilating a curved figure and stating the scale factor that would bring a dilated figure back to its original size.

Question 1.
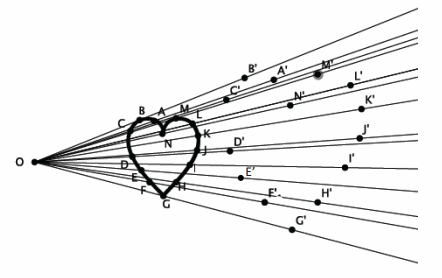
Dilate the figure from center O by a scale factor r=2. Make sure to use enough points to make a good image of the original figure.
Answer:
Sample student work is shown below. Verify that students used enough points to produce an image similar to the original.

Question 2.
Describe the process for selecting points when dilating a curved figure.
Answer:
When dilating a curved figure, you have to make sure to use a lot of points to produce a decent image of the original figure. You also have to make sure that the points you choose are not all concentrated in just one part of the figure.

Question 3.
A figure was dilated from center O by a scale factor of r=5. What scale factor would shrink the dilated figure back to the original size?
Answer:
A scale factor of r=\(\frac{1}{5}\) would bring the dilated figure back to its original size.

Question 4.
A figure has been dilated from center O by a scale factor of r=\(\frac{7}{6}\). What scale factor would shrink the dilated figure back to the original size?
A scale factor of r=\(\frac{6}{7}\) would bring the dilated figure back to its original size.

Question 5.
A figure has been dilated from center O by a scale factor of r=\(\frac{3}{10}\). What scale factor would magnify the dilated figure back to the original size?
Answer:
A scale factor of r=\(\frac{10}{3}\) would bring the dilated figure back to its original size.

Eureka Math Grade 8 Module 3 Lesson 3 Exit Ticket Answer Key

Question 1.
Dilate circle A from center O by a scale factor r=\(\frac{1}{2}\). Make sure to use enough points to make a good image of the original figure.

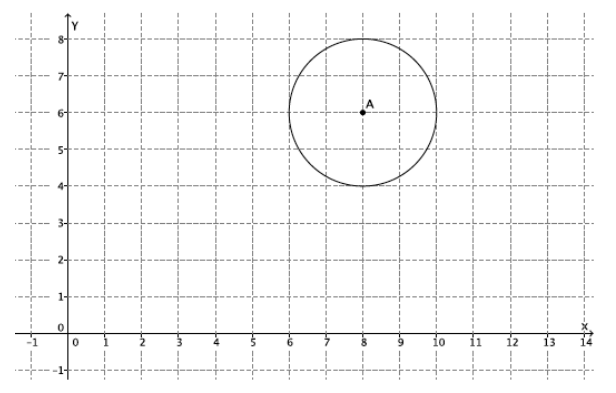
Answer:

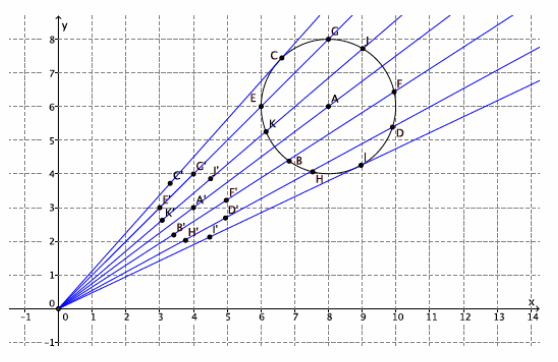
Student work is shown below. Verify that students used enough points to produce an image similar to the original.

Question 2.
What scale factor would magnify the dilated circle back to the original size of circle A? How do you know?
Answer:
A scale factor of r=2 would bring the dilated circle back to the size of circle A. Since the circle was dilated by a scale factor of r=\(\frac{1}{2}\), then to bring it back to its original size, you must dilate by a scale factor that is the reciprocal of \(\frac{1}{2}\), which is 2.