Engage NY Eureka Math 8th Grade Module 3 Lesson 2 Answer Key
Eureka Math Grade 8 Module 3 Lesson 2 Example Answer Key
Example 1.
Examples 1–3 demonstrate that dilations map lines to lines and how to use a compass to dilate.
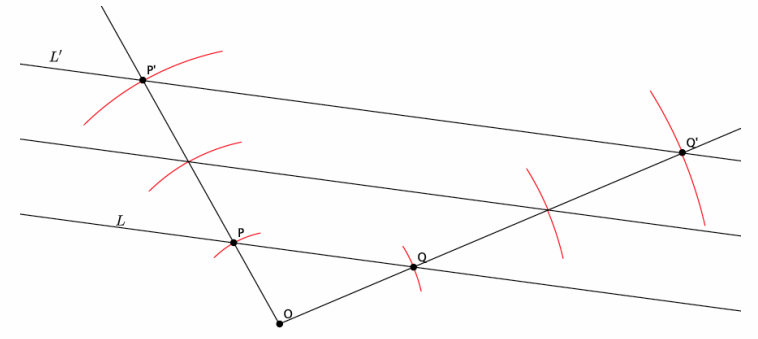
→ This example shows that a dilation maps a line to a line. This means that the image of a line, after undergoing a dilation, is also a line. Given line L, we dilate with a scale factor r=2 from center O. Before we begin, exactly how many lines can be drawn through two points?
→ Only one line can be drawn through two points.
To dilate the line, we choose two points on L (points P and Q) to dilate. When we connect the dilated images of P and Q (P’ and Q’), we have the dilated image of line L, L’.
→ First, let’s select a center O off the line L and two points P and Q on line L.
Examples 1–2:
Dilations Map Lines to Lines
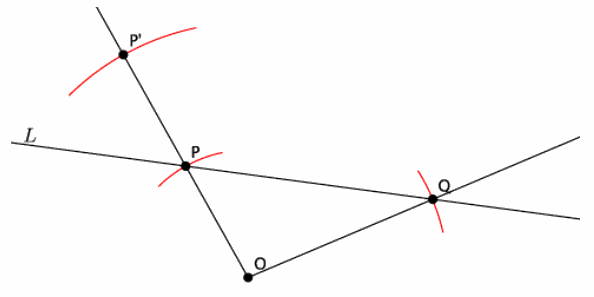
→ Second, we draw rays from center O through each of the points P and Q. We want to make sure that the points O, P, and P’ (the dilated P) lie on the same line (i.e., are collinear). That is what keeps the dilated image “in proportion.” Think back to the last lesson where we saw how the size of the picture changed when pulling the corners compared to the sides. Pulling from the corners kept the picture “in proportion.” The way we achieve this in diagrams is by drawing rays and making sure that the center, the point, and the dilated point are all on the same line.

→ Next, we use our compass to measure the distance from O to P. Do this by putting the point of the compass on point O, and adjust the radius of the compass to draw an arc through point P. Once you have the compass set, move the point of the compass to P, and make a mark along the ray OP (without changing the radius of the compass) to mark P’. Recall that the dilated point P’ is the distance 2|OP| (i.e., |OP’ |=2|OP|). The compass helps us to find the location of P’ so that it is exactly twice the length of segment OP. Use your ruler to prove this to students.
→ Next, we repeat this process to locate Q’.
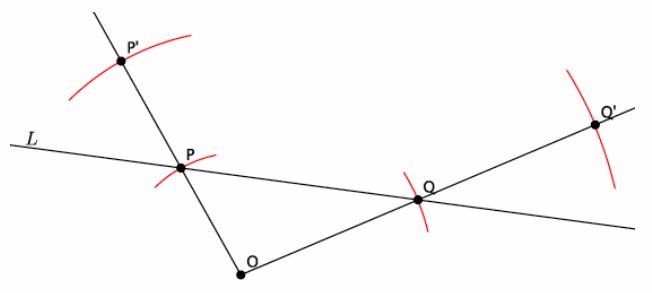
→ Finally, connect points P’ and Q’ to draw line L’.
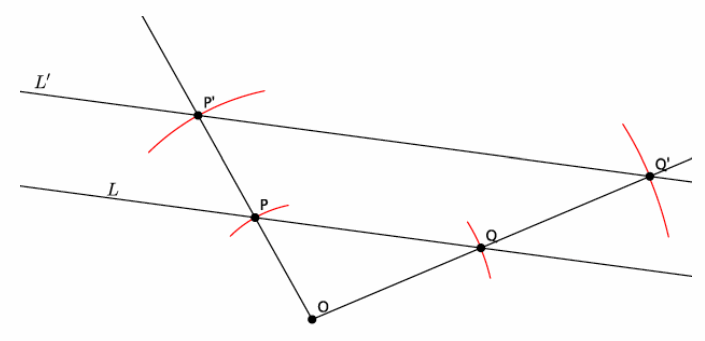
→ Return to your conjecture from before, or look at our class list. Which conjectures were accurate? How do you know?
→ Answers may vary depending on conjectures made by the class. Students should identify that the conjecture of a line mapping to a line under a dilation is correct.
→ What do you think would happen if we selected a different location for the center or for the points P and Q?
→ Points O, P, and Q are arbitrary points. That means that they could have been anywhere on the plane. For that reason, the results would be the same; that is, the dilation would still produce a line, and the line would be parallel to the original.
→ Look at the drawing again, and imagine using our transparency to translate the segment OP along vector \(\overrightarrow{O Q}\) to segment PP’ and to translate the segment OQ along vector \(\overrightarrow{O Q}\) to segment QQ’. With that information, can you say anything more about lines L and L’?
→ Since P and Q are arbitrary points on line L, and translations map lines to parallel lines when the vector is not parallel to or part of the original line, we can say that L is parallel to L’.
→ How would the work we did change if the scale factor were r=3 instead of r=2?
→ We would have to find a point P’ so that it is 3 times the length of segment OP instead of twice the length of segment OP. Same for the point Q’
Example 2.
→ Do you think line L would still be a line under a dilation with scale factor r=3? Would the dilated line, L’, still be parallel to L? (Allow time for students to talk to their partners and make predictions.)
→ Yes, it is still a line, and it would still be parallel to line L. The scale factor being three instead of two simply means that we would perform the translation of the points P’ and Q’ more than once, but the result would be the same.
→ Here is what would happen with scale factor r=3.
Example 3.
Dilations Map Lines to Lines

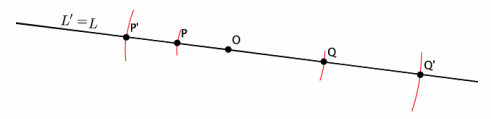
→ What would happen if the center O were on line L? (Allow time for students to talk to their partners and make predictions.)
→ If the center O were on line L, and if we pick points P and Q on L, then the dilations of points P and Q, P’ and Q’, would also be on L. That means that line L and its dilated image, line L’, would coincide.
→ What we have shown with these three examples is that a line, after a dilation, is still a line. Mathematicians like to say that dilations map lines to lines.
Example 4.
Example 4 demonstrates that dilations map rays to rays. It also demonstrates how to use a ruler to dilate with scale factor r=\(\frac{1}{2}\). Similar to Example 1, before this example, discuss the conjectures students developed about rays. Also, consider getting students started and then asking them to finish with a partner.
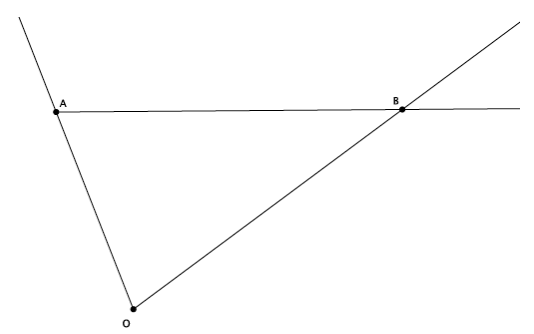
→ This example shows that a dilation maps a ray to a ray. Given ray \(\overrightarrow{A B}\), we dilate with a scale factor r=\(\frac{1}{2}\) from center O.
→ To dilate the ray, we choose a center O off of the ray. Like before, we draw rays from center O through points A and B.
→ Since our scale factor is r=\(\frac{1}{2}\), we need to use a ruler to measure the length of segments OA and OB. When you get into high school Geometry, you learn how to use a compass to handle scale factors that are greater than zero but less than one, like our r=\(\frac{1}{2}\). For now, we use a ruler.
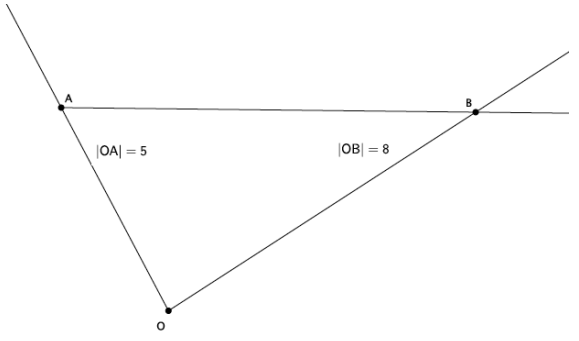
→ Since our scale factor is r=\(\frac{1}{2}\), we know that the dilated segment, OA’, must be equal to \(\frac{1}{2}\) the length of segment OA (i.e., |OA’ |=\(\frac{1}{2}\) |OA|). Then, |OA’ | must be \(\frac{1}{2}\)∙5; therefore, |OA’ |=2.5. What must the |OB’ | be?
→ We know that |OB’ |=\(\frac{1}{2}\) |OB|; therefore, |OB’ |=\(\frac{1}{2}\)⋅8=4, and |OB’ |=4.
→ Now that we know the lengths of segments OA’ and OB’, we use a ruler to mark off those points on their respective rays.
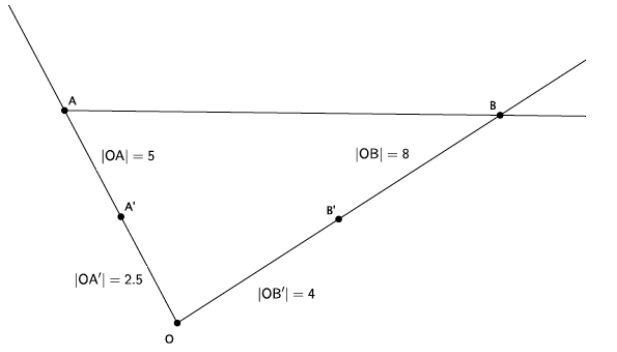
→ Finally, we connect point A’ through point B’. With your partner, evaluate your conjecture. What happened to our ray after the dilation?
→ When we connect point A’ through point B’, then we have the ray \(\overrightarrow{A^{\prime} B^{\prime}}\).
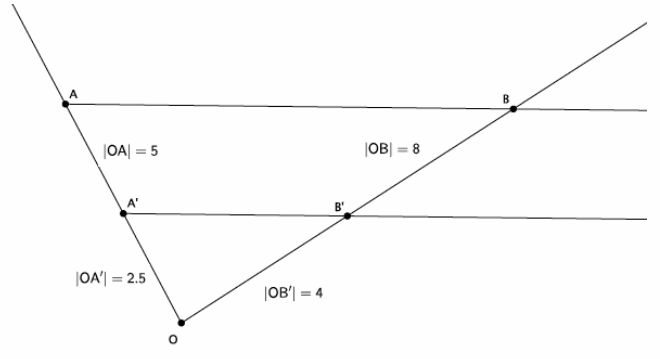
→ What do you think would have happened if we selected our center O as a point on the ray \(\overrightarrow{A B}\)?
→ If our center O were on the ray, then the ray \(\overrightarrow{A B}\) would coincide with its dilated image \(\overrightarrow{A^{\prime} B^{\prime}},\), which is similar to what we saw when the line L was dilated from a center O on it.

Eureka Math Grade 8 Module 3 Lesson 2 Exercise Answer Key
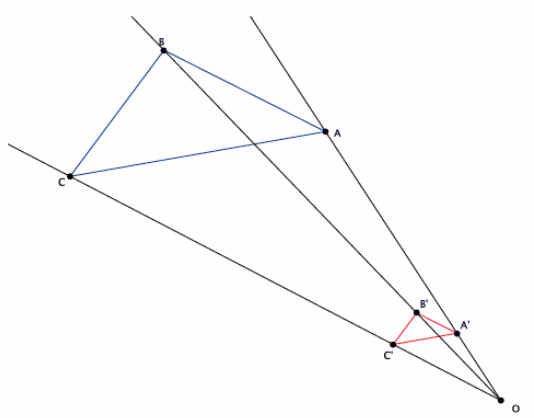
Given center O and triangle ABC, dilate the triangle from center O with a scale factor r=3.
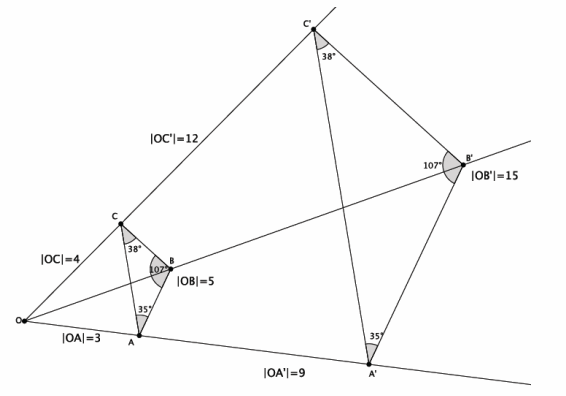
a. Note that the triangle ABC is made up of segments AB, BC, and CA. Were the dilated images of these segments still segments?
Answer:
Yes, when dilated, the segments were still segments.
b. Measure the length of the segments AB and A’ B’. What do you notice? (Think about the definition of dilation.)
Answer:
The segment A’ B’ was three times the length of segment AB. This fits with the definition of dilation, that is, |A’ B’ |=r|AB|.
c. Verify the claim you made in part (b) by measuring and comparing the lengths of segments BC and B’ C’ and segments CA and C’ A’. What does this mean in terms of the segments formed between dilated points?
Answer:
This means that dilations affect segments in the same way they do points. Specifically, the lengths of segments are dilated according to the scale factor.
d. Measure ∠ABC and ∠A’B’C’. What do you notice?
Answer:
The angles are equal in measure.
e. Verify the claim you made in part (d) by measuring and comparing the following sets of angles:
(1) ∠BCA and ∠B’ C’ A’ and
(2) ∠CAB and ∠C’ A’ B’. What does that mean in terms of dilations with respect to angles and their degrees?
Answer:
It means that dilations map angles to angles, and the dilation preserves the measures of the angles.
Eureka Math Grade 8 Module 3 Lesson 2 Exit Ticket Answer Key
Question 1.
Given center O and quadrilateral ABCD, using a compass and ruler, dilate the figure from center O by a scale factor of r=2. Label the dilated quadrilateral A’B’C’D’.
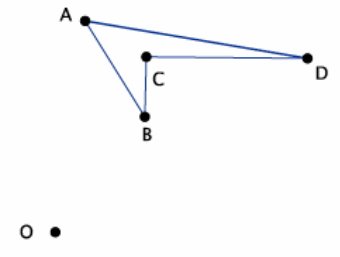
Answer:
Sample student work is shown below. Verify that students have magnified the image ABCD.
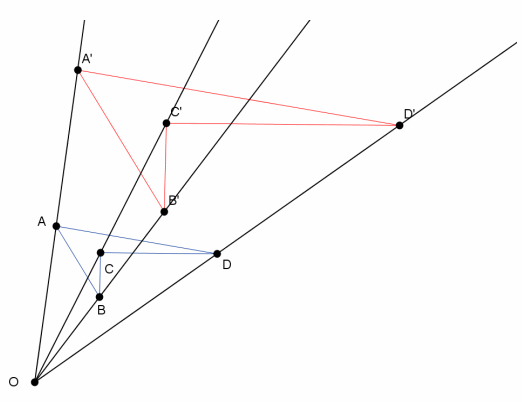
Question 2.
Describe what you learned today about what happens to lines, segments, rays, and angles after a dilation.
Answer:
We learned that a dilation maps a line to a line, a segment to a segment, a ray to a ray, and an angle to an angle. Further, the length of the dilated line segment is exactly r (the scale factor) times the length of the original segment. Also, the measure of a dilated angle remains unchanged compared to the original angle.
Eureka Math Grade 8 Module 3 Lesson 2 Problem Set Answer Key
Students practice dilating figures with different scale factors.
Question 1.
Use a ruler to dilate the following figure from center O, with scale factor r=\(\frac{1}{2}\).
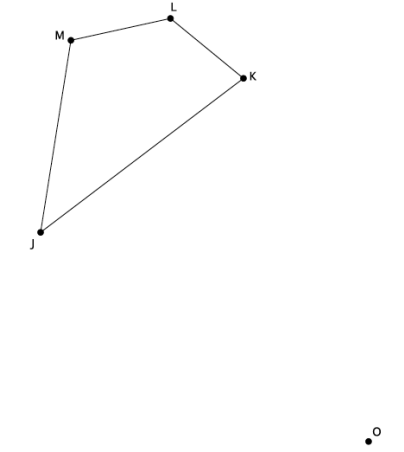
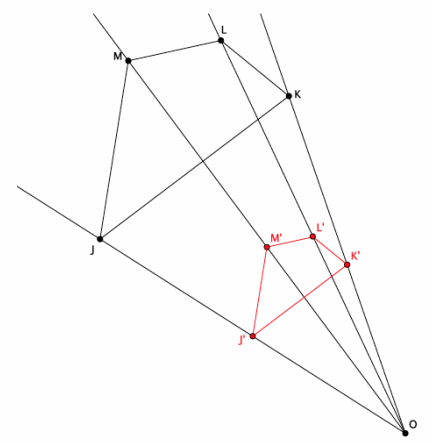
Answer:
The dilated figure is shown in red below. Verify that students have dilated according to the scale factor r=\(\frac{1}{2}\).
Question 2.
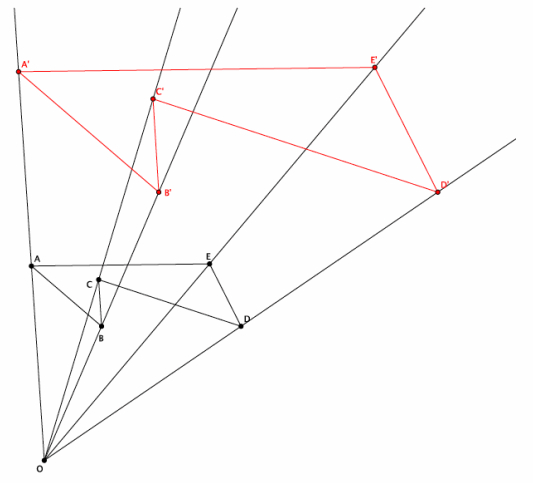
Use a compass to dilate the figure ABCDE from center O, with scale factor r=2.
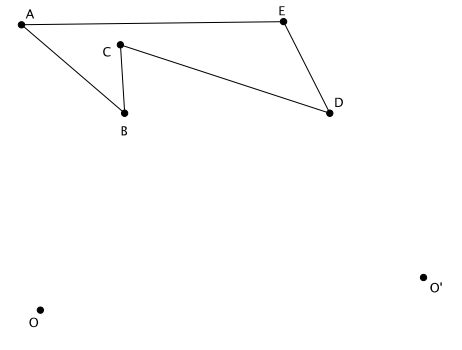
Answer:
The figure in red below shows the dilated image of ABCDE.
a. Dilate the same figure, ABCDE, from a new center, O’, with scale factor r=2. Use double primes (A”B”C”D”E”) to distinguish this image from the original.
Answer:
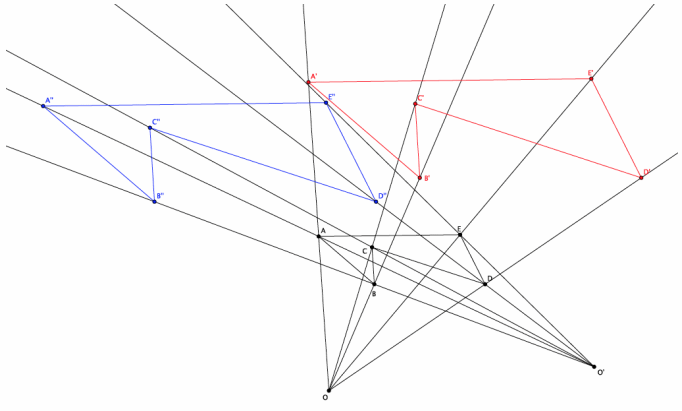
The figure in blue below shows the dilated figure A”B”C”D”E”.
b. What rigid motion, or sequence of rigid motions, would map A”B”C”D”E” to A’B’C’D’E’?
Answer:
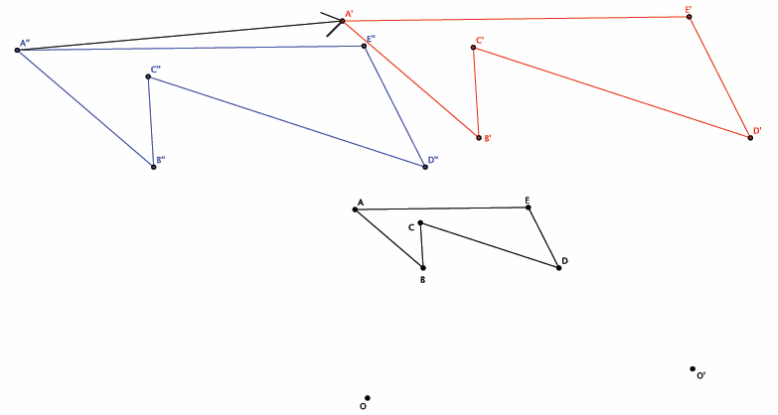
A translation along vector \(\overrightarrow{\boldsymbol{A}^{\prime \prime} \boldsymbol{A}^{\prime}}\) (or any vector that connects a point of A”B”C”D”E” and its corresponding point of A’B’C’D’E’) would map the figure A”B”C”D”E” to A’B’C’D’E’.
The image below (with rays removed for clarity) shows the vector \(\overrightarrow{\boldsymbol{A}^{\prime \prime} \boldsymbol{A}^{\prime}}\).
Question 3.
Given center O and triangle ABC, dilate the figure from center O by a scale factor of r=\(\frac{1}{4}\). Label the dilated triangle A’B’C’.
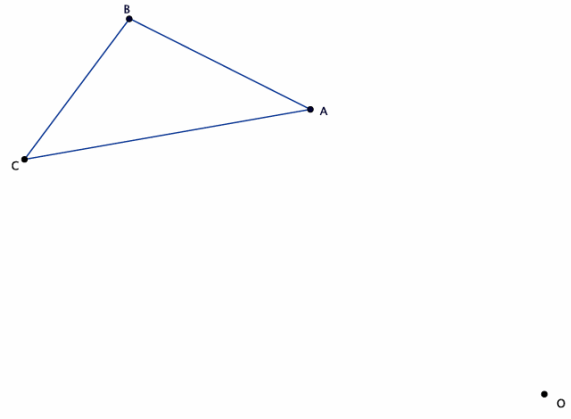
Answer:
Question 4.
A line segment AB undergoes a dilation. Based on today’s lesson, what is the image of the segment?
Answer:
The segment dilates as a segment.
Question 5.
∠GHI measures 78°. After a dilation, what is the measure of ∠G’H’I’? How do you know?
Answer:
The measure of ∠G’H’I’ is 78°. Dilations preserve angle measure, so it remains the same size as ∠GHI.