Engage NY Eureka Math 8th Grade Module 3 Lesson 14 Answer Key
Eureka Math Grade 8 Module 3 Lesson 14 Example Answer Key
Example 1.
To maintain the focus of the lesson, allow the use of calculators in order to check the validity of the right angle using the Pythagorean theorem.
→ The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle?
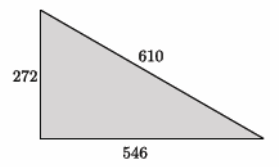
→ To find out, we need to put these numbers into the Pythagorean theorem. Recall that side c is always the longest side. Since 610 is the largest number, it is representing the c in the Pythagorean theorem. To determine if this triangle is a right triangle, then we need to verify the computation.

→ Find the value of the left side of the equation: 2722+5462=372 100. Then, find the value of the right side of the equation: 6102=372 100. Since the left side of the equation is equal to the right side of the equation, we have a true statement, that is, 2722+5462=6102. What does that mean about the triangle?
→ It means that the triangle with side lengths of 272, 546, and 610 is a right triangle.
Example 2.
→ The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle?
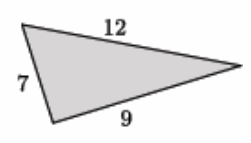
→ What do we need to do to find out if this is a right triangle?
→ We need to see if it makes a true statement when we replace a, b, and c with the numbers using the Pythagorean theorem.
→ Which number is c? How do you know?
→ The longest side is 12; therefore, c=12.
→ Use your calculator to see if it makes a true statement. (Give students a minute to calculate.) Is it a right triangle? Explain.
→ No, it is not a right triangle. If it were a right triangle, the equation 72+92=122 would be true. But the left side of the equation is equal to 130, and the right side of the equation is equal to 144. Since 130≠144, then these lengths do not form a right triangle.
Eureka Math Grade 8 Module 3 Lesson 14 Exercise Answer Key
Exercise 1.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
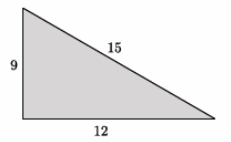
Answer:
We need to check if 92+122=152 is a true statement. The left side of the equation is equal to 225. The right side of the equation is equal to 225. That means 92+122=152 is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.
Exercise 2.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
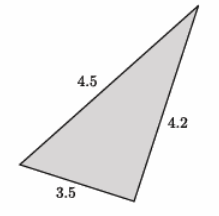
Answer:
We need to check if 3.52+4.22=4.52 is a true statement. The left side of the equation is equal to 29.89. The right side of the equation is equal to 20.25. That means 3.52+4.22=4.52 is not true, and the triangle shown is not a right triangle.
Exercise 3.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
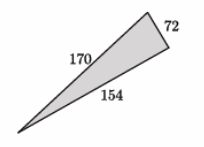
Answer:
We need to check if 722+1542=1702 is a true statement. The left side of the equation is equal to 28,900. The right side of the equation is equal to 28,900. That means 722+1542=1702 is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.
Exercise 4.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
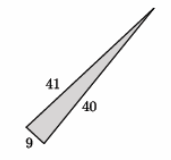
Answer:
We need to check if 92+402=412 is a true statement. The left side of the equation is equal to 1,681. The right side of the equation is equal to 1,681. That means 92+402=412 is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.
Exercise 5.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
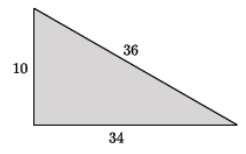
Answer:
We need to check if 102+342=362 is a true statement. The left side of the equation is equal to 1,256. The right side of the equation is equal to 1,296. That means 102+342=362 is not true, and the triangle shown is not a right triangle.
Exercise 6.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
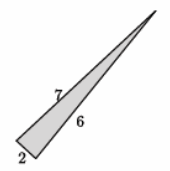
Answer:
We need to check if 22+52=72 is a true statement. The left side of the equation is equal to 29. The right side of the equation is equal to 49. That means 22+52=72 is not true, and the triangle shown is not a right triangle.
Exercise 7.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
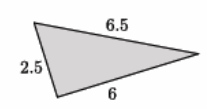
Answer:
We need to check if 2.52+62=6.52 is a true statement. The left side of the equation is equal to 42.25. The right side of the equation is equal to 42.25. That means 2.52+62=6.52 is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.
Eureka Math Grade 8 Module 3 Lesson 14 Exit Ticket Answer Key
Question 1.
The numbers in the diagram below indicate the lengths of the sides of the triangle. Bernadette drew the following triangle and claims it is a right triangle. How can she be sure?

Answer:
Since 37 is the longest side, if this triangle was a right triangle, 37 would have to be the hypotenuse (or c). Now she needs to check to see if 122+352=372 is a true statement. The left side is 1,369, and the right side is 1,369. That means 122+352=372 is true, and this is a right triangle.
Question 2.
Do the lengths 5, 9, and 14 form a right triangle? Explain.
Answer:
No, the lengths of 5, 9, and 14 do not form a right triangle. If they did, then the equation 52+92=142 would be a true statement. However, the left side equals 106, and the right side equals 196. Therefore, these lengths do not form a right triangle.
Eureka Math Grade 8 Module 3 Lesson 14 Problem Set Answer Key
Students practice using the converse of the Pythagorean theorem and identifying common errors in computations.
Question 1.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
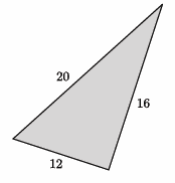
Answer:
We need to check if 122+162=202 is a true statement. The left side of the equation is equal to 400. The right side of the equation is equal to 400. That means 122+162=202 is true, and the triangle shown is a right triangle.
Question 2.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
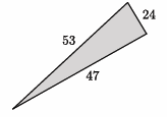
Answer:
We need to check if 472+242=532 is a true statement. The left side of the equation is equal to 2,785. The right side of the equation is equal to 2,809. That means 472+242=532 is not true, and the triangle shown is not a right triangle.
Question 3.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
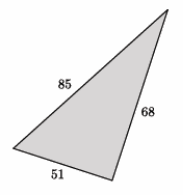
Answer:
We need to check if 512+682=852 is a true statement. The left side of the equation is equal to 7,225. The right side of the equation is equal to 7,225. That means 512+682=852 is true, and the triangle shown is a right triangle.
Question 4.
The numbers in the diagram below indicate the units of length of each side of the triangle. Sam said that the following triangle is a right triangle because 9+32=40. Explain to Sam what he did wrong to reach this conclusion and what the correct solution is.
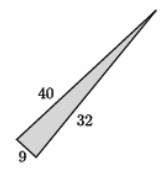
Answer:
Sam added incorrectly, but more importantly forgot to square each of the side lengths. In other words, he said 9+32=40, which is not a true statement. However, to show that a triangle is a right triangle, you have to use the Pythagorean theorem, which is a2+b2=c2. Using the Pythagorean theorem, the left side of the equation is equal to 1,105, and the right side is equal to 1,600. Since 1,105≠1,600, the triangle is not a right triangle.
Question 5.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.
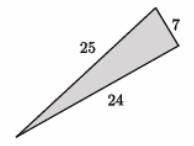
Answer:
We need to check if 242+72=252 is a true statement. The left side of the equation is equal to 625. The right side of the equation is equal to 625. That means 242+72=252 is true, and the triangle shown is a right triangle.
Question 6.
Jocelyn said that the triangle below is not a right triangle. Her work is shown below. Explain what she did wrong, and show Jocelyn the correct solution.
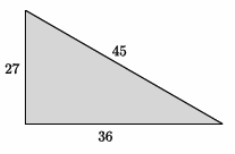
We need to check if 272+452=362 is a true statement. The left side of the equation is equal to 2,754. The right side of the equation is equal to 1,296. That means 272+452=362 is not true, and the triangle shown is not a right triangle.
Answer:
Jocelyn made the mistake of not putting the longest side of the triangle in place of c in the Pythagorean theorem, a2+b2=c2. Specifically, she should have used 45 for c, but instead she used 36 for c. If she had done that part correctly, she would have seen that, in fact, 272+362=452 is a true statement because both sides of the equation equal 2,025. That means that the triangle is a right triangle.