Engage NY Eureka Math 8th Grade Module 3 Lesson 12 Answer Key
Eureka Math Grade 8 Module 3 Lesson 12 Example Answer Key
Example.
Not all flagpoles are perfectly upright (i.e., perpendicular to the ground). Some are oblique (i.e., neither parallel nor at a right angle, slanted). Imagine an oblique flagpole in front of an abandoned building. The question is, can we use sunlight and shadows to determine the length of the flagpole?
Assume that we know the following information: The length of the shadow of the flagpole is 15 feet. There is a mark on the flagpole 3 feet from its base. The length of the shadow of this three-foot portion of the flagpole is 1.7 feet.
Answer:
Students may say that they would like to directly measure the length of the pole. Remind them a direct measurement may not always be possible.
→ Where would the shadow of the flagpole be?
→ On the ground, some distance from the base of the flagpole
→ In the picture below, OA is the length of the flagpole. OB is the length of the shadow cast by the flagpole. (OC) ̅ represents the segment from the base to the 3-foot mark up the flagpole, and OD is the length of the shadow cast by the length of (OC) ̅ that is 1.7 feet in length. (Note: The picture is not drawn to scale.)
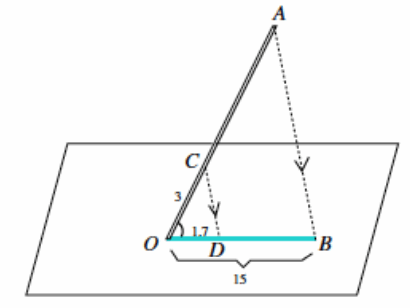
→ If we assume that all sunbeams are parallel to each other (i.e., \(\overline{C D}\)||\(\overline{A B}\)̅), do we have a pair of similar triangles? Explain.
→ If \(\overline{C D}\) || \(\overline{A B}\), then △COD~△AOB, by the AA criterion. Corresponding angles of parallel lines are equal, so we know that ∠CDO=∠ABO, and ∠COD is equal to itself.
→ Now that we know △COD~△AOB, how can we find the length of the flagpole?
→ Since the triangles are similar, then we know that the ratios of their corresponding sides must be equal. Therefore, if we let x represent the length of the flagpole (i.e., OA), then
\(\frac{x}{3}\)=\(\frac{15}{1.7}\)
→ We are looking for the value of x that makes the fractions equivalent.
→ Therefore, 1.7x=45, and x≈26.47. The length of the flagpole is approximately 26.47 feet.
Eureka Math Grade 8 Module 3 Lesson 12 Exercise Answer Key
Mathematical Modeling Exercises 1–3
Exercise 1.
You want to determine the approximate height of one of the tallest buildings in the city. You are told that if you place a mirror some distance from yourself so that you can see the top of the building in the mirror, then you can indirectly measure the height using similar triangles. Let point O be the location of the mirror so that the person shown can see the top of the building.
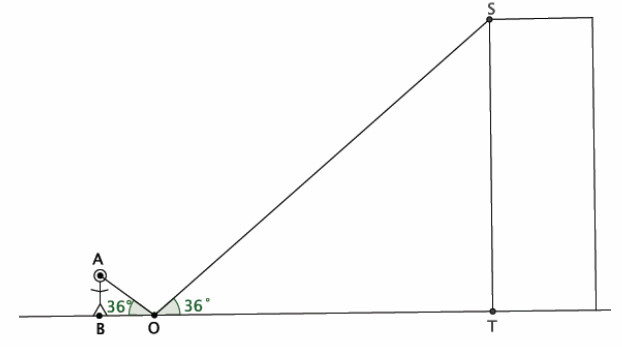
a. Explain why △ABO~△STO.
Answer:
The triangles are similar by the AA criterion. The angle that is formed by the figure standing is 90° with the ground. The building also makes a 90° angle with the ground. The measure of the angle formed with the mirror at ∠AOB is equal to the measure of ∠SOT. Since there are two pairs of corresponding angles that are equal in measure, then △ABO~△STO.
b. Label the diagram with the following information: The distance from eye level straight down to the ground is 5.3 feet. The distance from the person to the mirror is 7.2 feet. The distance from the person to the base of the building is 1,750 feet. The height of the building is represented by x.
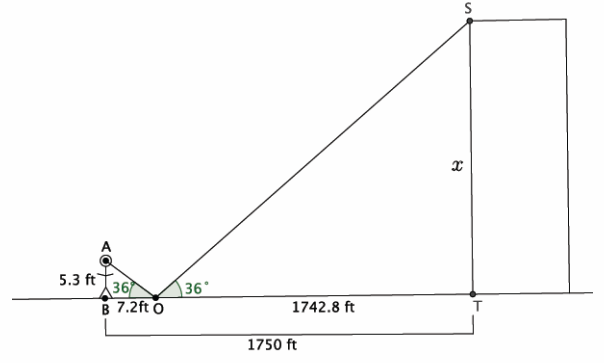
c. What is the distance from the mirror to the building?
Answer:
1750 ft.-7.2 ft.=1742.8 ft.
d. Do you have enough information to determine the approximate height of the building? If yes, determine the approximate height of the building. If not, what additional information is needed?
Answer:
Yes, there is enough information about the similar triangles to determine the height of the building.
Since x represents the height of the building, then
\(\frac{x}{5.3}\) = \(\frac{1,742.8}{7.2}\)
We are looking for the value of x that makes the fractions equivalent. Then, 7.2x=9236.84, and
x≈1282.9. The height of the building is approximately 1,282.9 feet.
Exercise 2.
A geologist wants to determine the distance across the widest part of a nearby lake. The geologist marked off specific points around the lake so that the line containing \(\overline{D E}\) would be parallel to the line containing \(\overline{B C}\). The segment BC is selected specifically because it is the widest part of the lake. The segment DE is selected specifically because it is a short enough distance to easily measure. The geologist sketched the situation as shown below.
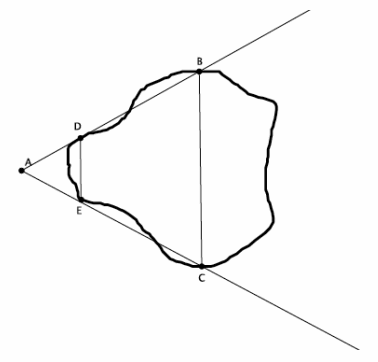
a. Has the geologist done enough work so far to use similar triangles to help measure the widest part of the lake? Explain.
Answer:
Yes, based on the sketch, the geologist found a center of dilation at point A. The geologist marked points around the lake that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠DAE is equal to itself. Since there are two pairs of corresponding angles that are equal, then △DAE~△BAC.
b. The geologist has made the following measurements: |DE|=5 feet, |AE|=7 feet, and |EC|=15 feet. Does she have enough information to complete the task? If so, determine the length across the widest part of the lake. If not, state what additional information is needed.
Answer:
Yes, there is enough information about the similar triangles to determine the distance across the widest part of the lake.
Let x represent the length of segment BC; then
\(\frac{x}{5}\)=\(\frac{22}{7}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 7x=110, and x≈15.7. The distance across the widest part of the lake is approximately 15.7 feet.
c. Assume the geologist could only measure a maximum distance of 12 feet. Could she still find the distance across the widest part of the lake? What would need to be done differently?
Answer:
The geologist could still find the distance across the widest part of the lake. However, she would have to select different points D and E at least 3 feet closer to points B and C, respectively. That would decrease the length of \(\overline{\boldsymbol{E C}}\) to, at most, 12 feet. Then \(\overline{\boldsymbol{D E}}\), in its new position, would still have to be contained within a line that was parallel to the line containing \(\overline{\boldsymbol{B C}}\) in order to calculate the desired distance.
Exercise 3.
A tree is planted in the backyard of a house with the hope that one day it is tall enough to provide shade to cool the house. A sketch of the house, tree, and sun is shown below.

a. What information is needed to determine how tall the tree must be to provide the desired shade?
Answer:
We need to ensure that we have similar triangles. For that reason, we need to know the height of the house and the length of the shadow that the house casts. We also need to know how far away the tree was planted from that point (i.e., the center). Assuming the tree grows perpendicular to the ground, the height of the tree and the height of the house would be parallel, and by the AA criterion, we would have similar triangles.
b. Assume that the sun casts a shadow 32 feet long from a point on top of the house to a point in front of the house. The distance from the end of the house’s shadow to the base of the tree is 53 feet. If the house is 16 feet tall, how tall must the tree get to provide shade for the house?
Answer:
If we let x represent the height the tree must be, then
\(\frac{16}{x}\)=\(\frac{32}{53}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 32x=848, and x=26.5. The tree must grow to a height of 26.5 feet to provide the desired shade for the house.
c. Assume that the tree grows at a rate of 2.5 feet per year. If the tree is now 7 feet tall, about how many years will it take for the tree to reach the desired height?
Answer:
The tree needs to grow an additional 19.5 feet to reach the desired height. If the tree grows 2.5 feet per year, then it will take the tree 7.8 years or about 8 years to reach a height of 26.5 feet.
Eureka Math Grade 8 Module 3 Lesson 12 Problem Set Answer Key
Students practice solving real-world problems using properties of similar triangles.
Question 1.
The world’s tallest living tree is a redwood in California. It’s about 370 feet tall. In a local park, there is a very tall tree. You want to find out if the tree in the local park is anywhere near the height of the famous redwood.
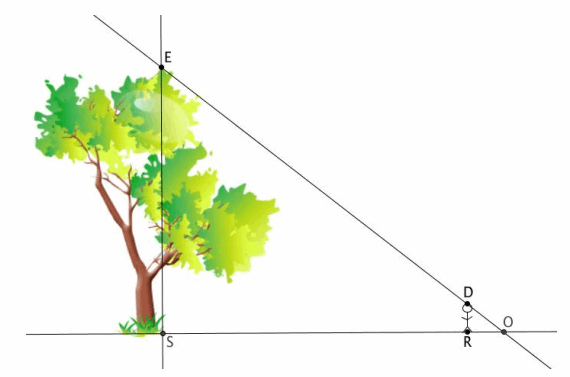
a. Describe the triangles in the diagram, and explain how you know they are similar or not.
Answer:
There are two triangles in the diagram, one formed by the tree and the shadow it casts, △ESO, and another formed by the person and his shadow, △DRO. The triangles are similar if the height of the tree is measured at a 90° angle with the ground and if the person standing forms a 90° angle with the ground. We know that ∠DOR is an angle common to both triangles. If ∠ESO=∠DRO=90°, then △ESO~△DRO by the AA criterion.
b. Assume △ESO~△DRO. A friend stands in the shadow of the tree. He is exactly 5.5 feet tall and casts a shadow of 12 feet. Is there enough information to determine the height of the tree? If so, determine the height. If not, state what additional information is needed.
Answer:
No, there is not enough information to determine the height of the tree. I need either the total length of the shadow that the tree casts or the distance between the base of the tree and the friend.
c. Your friend stands exactly 477 feet from the base of the tree. Given this new information, determine about how many feet taller the world’s tallest tree is compared to the one in the local park.
Let x represent the height of the tree; then
\(\frac{x}{5.5}\)=\(\frac{489}{12}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 12x=2689.5, and x=224.125. The world’s tallest tree is about 146 feet taller than the tree in the park.
d. Assume that your friend stands in the shadow of the world’s tallest redwood, and the length of his shadow is just 8 feet long. How long is the shadow cast by the tree?
Answer:
Let x represent the length of the shadow cast by the tree; then
\(\frac{x}{8}\)=\(\frac{370}{5.5}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 5.5x=2960, and
x≈538.2. The shadow cast by the world’s tallest tree is about 538 feet in length.
Question 2.
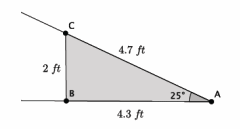
A reasonable skateboard ramp makes a 25° angle with the ground. A two-foot-tall ramp requires about 4.3 feet of wood along the base and about 4.7 feet of wood from the ground to the top of the two-foot height to make the ramp.
a. Sketch a diagram to represent the situation.
Answer:
A sample student drawing is shown below.
b. Your friend is a daredevil and has decided to build a ramp that is 5 feet tall. What length of wood is needed to make the base of the ramp? Explain your answer using properties of similar triangles.
Answer:
Sample student drawing and work are shown below.
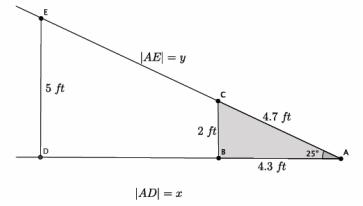
△EDA~△CBA by the AA criterion because ∠A is common to both triangles, and ∠EDA=∠CBA=90°.
If we let x represent the base of the 5-foot ramp, then
\(\frac{4.3}{x}\)=\(\frac{2}{5}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 2x=21.5, and x=10.75. The base of the 5-foot ramp must be 10.75 feet in length.
c. What length of wood is required to go from the ground to the top of the 5-foot height to make the ramp? Explain your answer using properties of similar triangles.
Answer:
If we let y represent the length of the wood needed to make the ramp, then
\(\frac{4.7}{y}\)=\(\frac{2}{5}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 2y=23.5, and
y=11.75. The length of wood needed to make the ramp is 11.75 feet.
Eureka Math Grade 8 Module 3 Lesson 12 Exit Ticket Answer Key
Henry thinks he can figure out how high his kite is while flying it in the park. First, he lets out 150 feet of string and ties the string to a rock on the ground. Then, he moves from the rock until the string touches the top of his head. He stands up straight, forming a right angle with the ground. He wants to find out the distance from the ground to his kite. He draws the following diagram to illustrate what he has done.
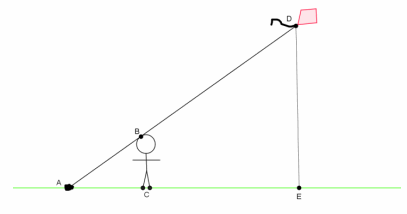
a. Has Henry done enough work so far to use similar triangles to help measure the height of the kite? Explain.
Answer:
Yes Based on the sketch, Henry found a center of dilation, point A. Henry has marked points so that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠BAC is equal to itself. Since there are two pairs of corresponding angles that are equal, then △BAC~△DAE.
b. Henry knows he is 5\(\frac{1}{2}\) feet tall. Henry measures the string from the rock to his head and finds it to be 8 feet. Does he have enough information to determine the height of the kite? If so, find the height of the kite. If not, state what other information would be needed.
Answer:
Yes, there is enough information. Let x represent the height DE. Then,
\(\frac{8}{150}\)=\(\frac{5.5}{x}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 8x=825, and x=103.125 feet. The height of the kite is approximately 103 feet high in the air.