Engage NY Eureka Math 8th Grade Module 3 Lesson 11 Answer Key
Eureka Math Grade 8 Module 3 Lesson 11 Exercise Answer Key
Exercise 1.
In the diagram below, you have △ABC and △AB’ C’. Use this information to answer parts (a)–(d).
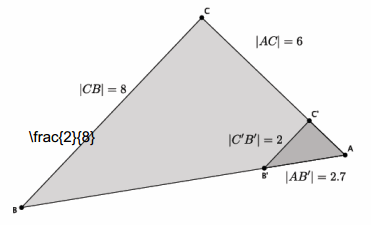
a. Based on the information given, is △ABC~△AB’ C’? Explain.
Answer:
There is not enough information provided to determine if the triangles are similar. We would need information about a pair of corresponding angles or more information about the side lengths of each of the triangles.
b. Assume the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\). With this information, can you say that △ABC~△AB’ C’? Explain.
Answer:
If the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\), then △ABC~△AB’ C’. Both triangles share ∠A. Another pair of equal angles is ∠AB’C’and ∠ABC. They are equal because they are corresponding angles of parallel lines. By the AA criterion, △ABC~△AB’ C’.
c. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A C^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{A C^{\prime}}\).
\(\frac{x}{6}\)=\(\frac{2}{8}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 8x=12, and x=1.5.
The length of side \(\overline{A C^{\prime}}\) is 1.5.
d. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A B}\).
Answer:
Let y represent the length of side \(\overline{A B}\).
\(\frac{2.7}{y}\)=\(\frac{2}{8}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 2y=21.6, and y=10.8. The length of side \(\overline{A B}\) is 10.8.
Exercise 2.
In the diagram below, you have △ABC and △A’B’C’. Use this information to answer parts (a)–(c).
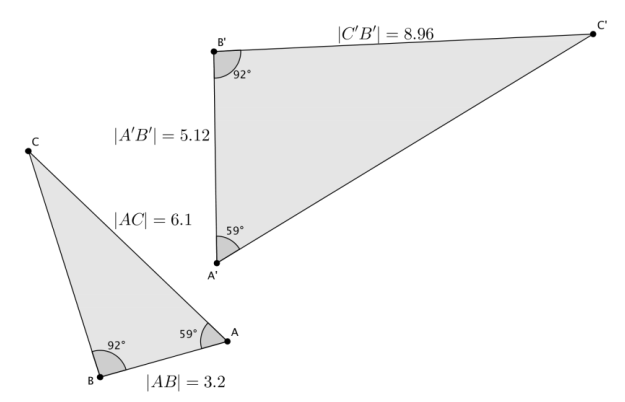
a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’ B’C’. There are two pairs of corresponding angles that are equal in measure, namely, ∠A=∠A’=59°, and ∠B=∠B’=92°. By the AA criterion, these triangles are similar.
b. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{A^{\prime} C^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{A^{\prime} C^{\prime}}\).
\(\frac{x}{6.1}\)=\(\frac{5.12}{3.2}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 3.2x=31.232, and
x=9.76. The length of side \(\overline{A^{\prime} C^{\prime}}\) is 9.76.
c. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{B C}\).
Answer:
Let y represent the length of side \(\overline{B C}\).
\(\frac{8.96}{y}\)=\(\frac{5.12}{3.2}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 5.12y=28.672, and y=5.6. The length of side \(\overline{B C}\) is 5.6.
Exercise 3.
In the diagram below, you have △ABC and △A’B’ C’. Use this information to answer the question below.
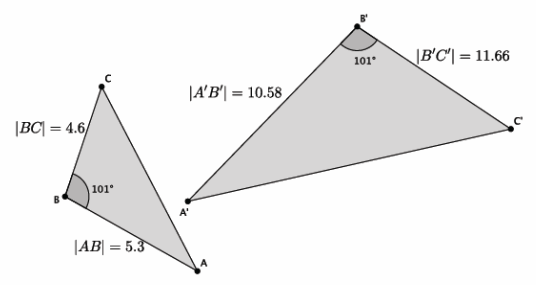
Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
No, △ABC is not similar to △A’ B’ C’. Since there is only information about one pair of corresponding angles, then we must check to see that the corresponding sides have equal ratios. That is, the following must be true:
\(\frac{10.58}{5.3}\) = \(\frac{11.66}{4.6}\)
When we compare products of each numerator with the denominator of the other fraction, we see that 48.668≠61.798. Since the corresponding sides do not have equal ratios, then the fractions are not equivalent, and the triangles are not similar.
Eureka Math Grade 8 Module 3 Lesson 11 Problem Set Answer Key
Students practice presenting informal arguments as to whether or not two given triangles are similar. Students practice finding measurements of similar triangles.
Question 1.
In the diagram below, you have △ABC and △A’B’ C’. Use this information to answer parts (a)–(b).
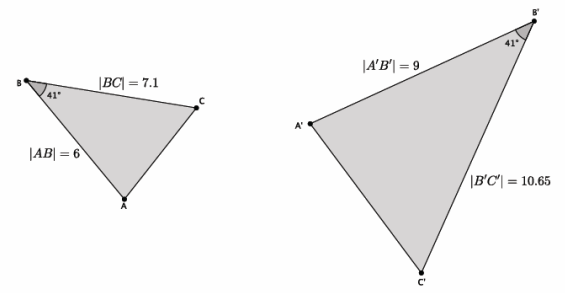
a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’B’ C’. Since there is only information about one pair of corresponding angles being equal, then the corresponding sides must be checked to see if their ratios are equal.
\(\frac{10.65}{7.1}\)=\(\frac{9}{6}\)
63.9=63.9
Since the cross products are equal, the triangles are similar.
b. Assume the length of side \(\overline{A C}\) is 4.3. What is the length of side \(\overline{A^{\prime} C^{\prime}}\)?
Answer:
Let x represent the length of side \(\overline{A^{\prime} C^{\prime}}\).
\(\frac{x}{4.3}\)=\(\frac{9}{6}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 6x=38.7, and x=6.45. The length of side \(\overline{A^{\prime} C^{\prime}}\) is 6.45.
Question 2.
In the diagram below, you have △ABC and △AB’ C’. Use this information to answer parts (a)–(d).
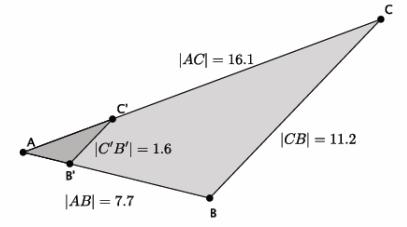
a. Based on the information given, is △ABC~△AB’ C’? Explain.
Answer:
There is not enough information provided to determine if the triangles are similar. We would need information about a pair of corresponding angles or more information about the side lengths of each of the triangles.
b. Assume the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\). With this information, can you say that △ABC~△AB’ C’? Explain.
Answer:
If the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\), then △ABC~△AB’ C’. Both triangles share ∠A. Another pair of equal angles are ∠AB’C’ and ∠ABC. They are equal because they are corresponding angles of parallel lines. By the AA criterion, △ABC~△AB’ C’.
c. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A C^{\prime}}\).
Let x represent the length of side \(\overline{A C^{\prime}}\).
\(\frac{x}{16.1}\)=\(\frac{1.6}{11.2}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 11.2x=25.76, and x=2.3. The length of side \(\overline{A C^{\prime}}\) is 2.3.
d. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A B^{\prime}}\).
Answer:
Let y represent the length of side \(\overline{A B^{\prime}}\).
\(\frac{y}{7.7}\)=\(\frac{1.6}{11.2}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 11.2y=12.32, and
y=1.1. The length of side \(\overline{A B^{\prime}}\) is 1.1.
Question 3.
In the diagram below, you have △ABC and △A’B’ C’. Use this information to answer parts (a)–(c).
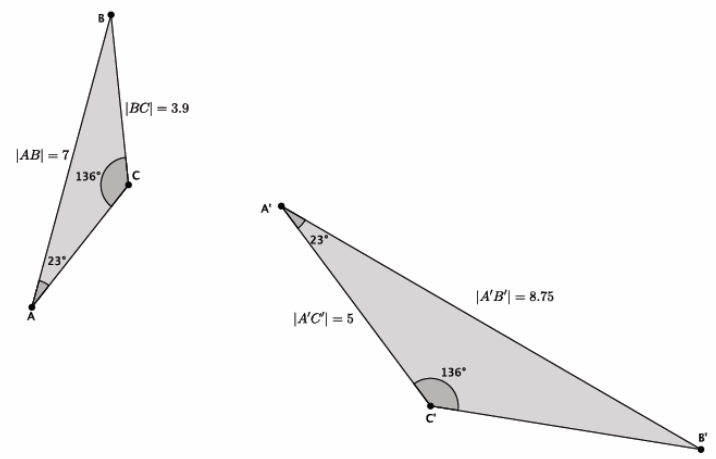
a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’ B’C’. There are two pairs of corresponding angles that are equal in measure, namely, ∠A=∠A’=23°, and ∠C=∠C’=136°. By the AA criterion, these triangles are similar.
b. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\).
\(\frac{x}{3.9}\)=\(\frac{8.75}{7}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 7x=34.125, and
x=4.875. The length of side \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\) is 4.875.
c. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{A C}\).
Answer:
Let y represent the length of side \(\overline{A C}\).
\(\frac{5}{y}\)=\(\frac{8.75}{7}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 8.75y=35, and y=4. The length of side \(\overline{A C}\) is 4.
Question 4.
In the diagram below, you have △ABC and △AB’ C’. Use this information to answer the question below.
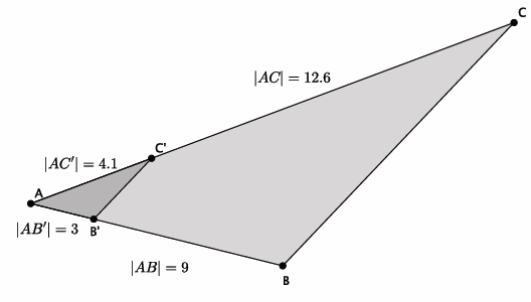
Based on the information given, is △ABC~△AB’ C’? Explain.
Answer:
No, △ABC is not similar to △AB’ C’. Since there is only information about one pair of corresponding angles, then we must check to see that the corresponding sides have equal ratios. That is, the following must be true:
\(\frac{9}{3}\)=\(\frac{12.6}{4.1}\)
When we compare products of each numerator with the denominator of the other fraction, we see that
36.9≠37.8. Since the corresponding sides do not have equal ratios, the fractions are not equivalent, and the triangles are not similar.
Question 5.
In the diagram below, you have △ABC and △A’B’C’. Use this information to answer parts (a)–(b).
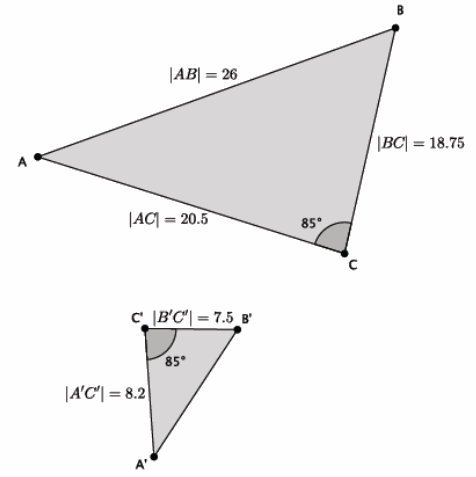
a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’B’ C’. Since there is only information about one pair of corresponding angles being equal, then the corresponding sides must be checked to see if their ratios are equal.
\(\frac{8.2}{20.5}\)=\(\frac{7.5}{18.75}\)
When we compare products of each numerator with the denominator of the other fraction, we see that 153.75=153.75. Since the products are equal, the fractions are equivalent, and the triangles are similar.
b. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\).
\(\frac{x}{26}\)=\(\frac{7.5}{18.75}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 18.75x=195, and
x=10.4. The length of side \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\) is 10.4.
Eureka Math Grade 8 Module 3 Lesson 11 Exit Ticket Answer Key
Question 1.
In the diagram below, you have △ABC and △A’B’ C’. Based on the information given, is △ABC~△A’B’ C’? Explain.
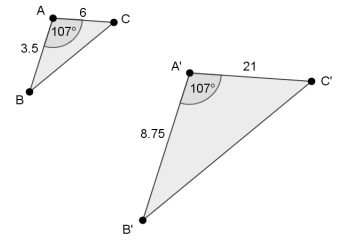
Answer:
Since there is only information about one pair of corresponding angles, we need to check to see if corresponding sides have equal ratios. That is, does \(\frac{|A B|}{\left|A^{\prime} B^{\prime}\right|}\) = \(\frac{|A C|}{\left|A^{\prime} C^{\prime}\right|^{\prime}}\), or does \(\frac{3.5}{8.75}\) = \(\frac{6}{21}\)? The products are not equal; 73.5≠52.5. Since the corresponding sides do not have equal ratios, the triangles are not similar.
Question 2.
In the diagram below, △ABC~△DEF. Use the information to answer parts (a)–(b).
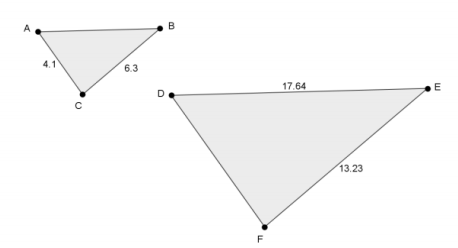
a. Determine the length of side \(\overline{A B}\). Show work that leads to your answer.
Answer:
Let x represent the length of side \(\overline{A B}\).
Then, \(\frac{x}{17.64}\)=\(\frac{6.3}{13.23}\). We are looking for the value of x that makes the fractions equivalent. Therefore, 111.132=13.23x, and x=8.4. The length of side \(\overline{A B}\) is 8.4.
b. Determine the length of side \(\overline{D F}\). Show work that leads to your answer.
Answer:
Let y represent the length of side \(\overline{D F}\).
Then, \(\frac{4.1}{y}\)= \(\frac{6.3}{13.23}\). We are looking for the value of y that makes the fractions equivalent. Therefore, 54.243=6.3y, and 8.61=y. The length of side \(\overline{D F}\) is 8.61.