Engage NY Eureka Math 8th Grade Module 3 End of Module Assessment Answer Key
Eureka Math Grade 8 Module 3 End of Module Assessment Task Answer Key
Question 1.
Use the diagram below to answer the questions that follow.
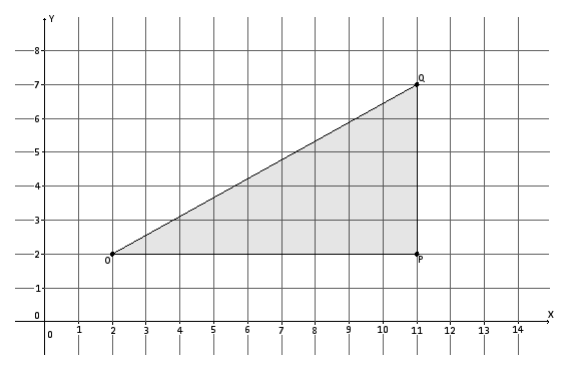
Answer:
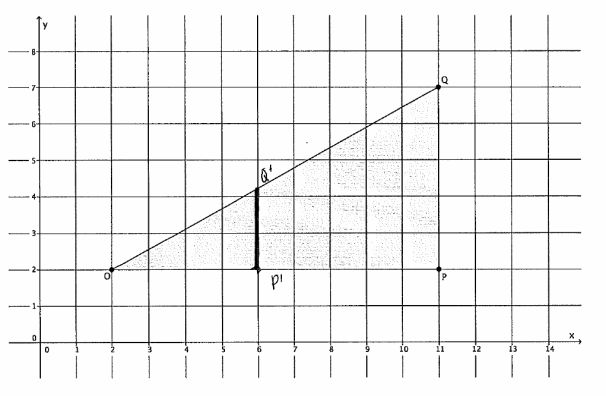
a. Dilate â–³OPQ from center O and scale factor r=\(\frac{4}{9}\). Label the image â–³OP’Q’.
b. Find the coordinates of points P’ and Q’.
Answer:
P’ = (6, 2)
Q’ = (6, \(\frac{38}{9}\))
\(\frac{\left(P^{\prime} Q^{\prime}\right)}{|P Q|}\) = \(\frac{4}{9}\)
\(\frac{\left|P^{\prime} Q^{\prime}\right|}{5}\) = \(\frac{4}{9}\)
|P’Q’| = \(\frac{20}{9}\)
\(\frac{20}{9}\) + 2 = \(\frac{20}{9}\) + \(\frac{18}{9}\)
= \(\frac{38}{9}\)
c. Are ∠OQP and ∠OQ’P’ equal in measure? Explain.
Answer:
Yes ∠OQP = ∠OQ’P’ Since D(â–³OQP) = â–³OQ’P’ and dilations are degree preserving, then ∠OQP = ∠OQ’P’.
∠OQP & ∠OQ’P’ are corresponding angles of parallel lines PQ & P’Q’, therefore ∠OQR = ∠OQ’P’
d. What is the relationship between segments PQ and P’Q’? Explain in terms of similar triangles.
Answer:
The lines that contain \(\overline{\text { PQ }}\) and \(\overline{p^{\prime} Q^{\prime}}\) are parallel. ∆OPQ ~ ∆OP’Q’ by the AA criterion (∠D = ∠D, ∠OP’Q’ = ∠OPQ), Therefore by the fundamental theorem of similarity \(\overline{P Q}\) || \(\overline{P^{\prime} Q^{\prime}}\)
e. If the length of segment OQ is 9.8 units, what is the length of segment OQ’? Explain in terms of similar triangles.
Answer:
Since ∆OPQ ~ ∆OP’Q’, then the ratios of lengths of corresponding sides will be equal to the scale factor then
\(\frac{\left|O P^{\prime}\right|}{|O P|}\) = \(\frac{\left|O Q^{\prime}\right|}{|O Q|}\) = \(\frac{4}{9}\)
\(\frac{4}{9}\) = \(\frac{\left|O Q^{\prime}\right|}{|9.0|}\)
39.2 = 9(|OQ’|)
4.36 = |OQ’|
|OQ’| is approximately 4.4 units.
Question 2.
Use the diagram below to answer the questions that follow. The length of each segment is as follows: segment OX is 5 units, segment OY is 7 units, segment XY is 3 units, and segment X’Y’ is 12.6 units.
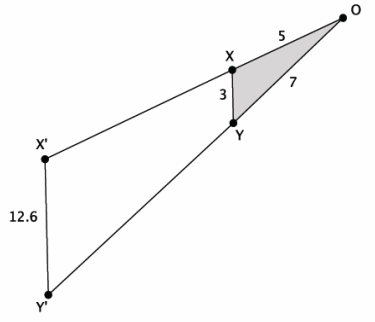
a. Suppose segment XY is parallel to segment X’Y’. Is â–³OXY similar to â–³OX’Y’? Explain.
Answer:
Yes, ∆OXY ~ ∆OX’Y’. Since \(\overline{X Y}\) || \(X^{\prime} Y^{\prime}\) and ∠OYX = ∠OY’X’. Because corresponding angles of parallel lines are equal in measure, by AA ∆OXY ~ ∆OX’Y’.
b. What is the length of segment OX’? Show your work.
Answer:
\(\frac{12.6}{3}\) = \(\frac{\left|O X^{\prime}\right|}{|5|}\)
5(12.6) = 3(|OX’|)
63 = 3(|OX’|)
21 = |OX’|
|OX’| is 21 units.
c. What is the length of segment OY’? Show your work.
Answer:
\(\frac{12.6}{3}\) = \(\frac{\left|OY^{\prime}\right|}{|7|}\)
12.6(7) = (3|OY’|)
88.2 = 3(|OY’|)
29.4 = |OY’|
|OY’| is 29.4 units.
Question 3.
Given â–³ABC ~â–³A^’ B^’ C’ and â–³ABC ~â–³A”B”C” in the diagram below, answer parts (a)–(c).
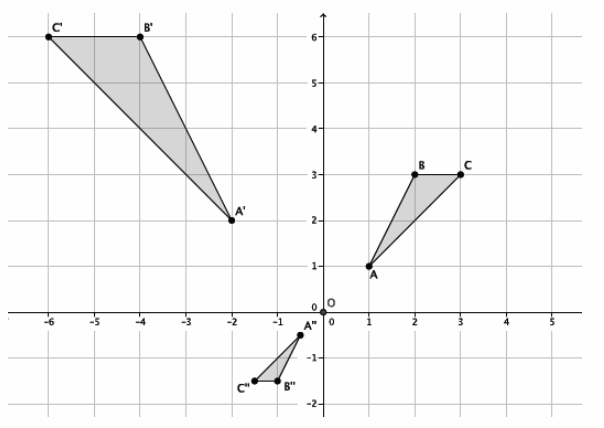
a. Describe the sequence that shows the similarity for â–³ABC and â–³A’ B’ C’.
Answer:
\(\frac{B^{\prime} C^{\prime}}{B C}\) = \(\frac{2}{1}\) = 2 = r
Le D be the dilation from center O and scale factor r=2. Let there be a reflection across the Y-axis. Then the dilation followed by the reflection maps â–³ABC onto â–³A’B’C’.
b. Describe the sequence that shows the similarity for â–³ABC and â–³A”B”C”.
Answer:
Let D be the dilation from center O and scale factor. 0<r<1. Let there be a rotation of 180° around center O. Then the dilation followed by the rotation maps â–³ABC onto â–³A”B”C”.
c. Is â–³A’B’C’ similar to â–³A”B”C”? How do you know?
Answer:
Yes â–³A’B’C’ ~ â–³A”B”C”. Dilations preserve angle measures and since â–³ABC ~ â–³A’B’C and â–³ABC ~ â–³A”B”C”, we know ∠A= ∠A’ = ∠A”, ∠B = ∠B’=∠B”, by AA Criterion for similarity â–³A’B’C’ ~ â–³ A”B”C”. Also, similarity is Transitive.