Engage NY Eureka Math 8th Grade Module 2 Mid Module Assessment Answer Key
Eureka Math Grade 8 Module 2 Mid Module Assessment Task Answer Key
Question 1.
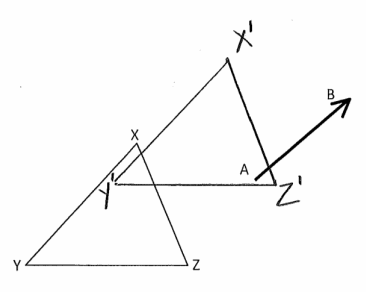
Translate △XYZ along \(\overrightarrow{A B}\). Label the image of the triangle with X’, Y’, and Z’.
Answer:
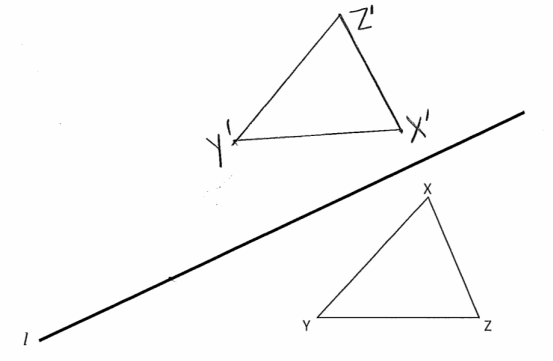
b. Reflect △XYZ across the line of reflection, l. Label the image of the triangle with X’, Y’, and Z’.
Answer:
c. Rotate △XYZ around the point (1,0) clockwise 90°. Label the image of the triangle with X’, Y’, and Z’.
Answer:
Question 2.
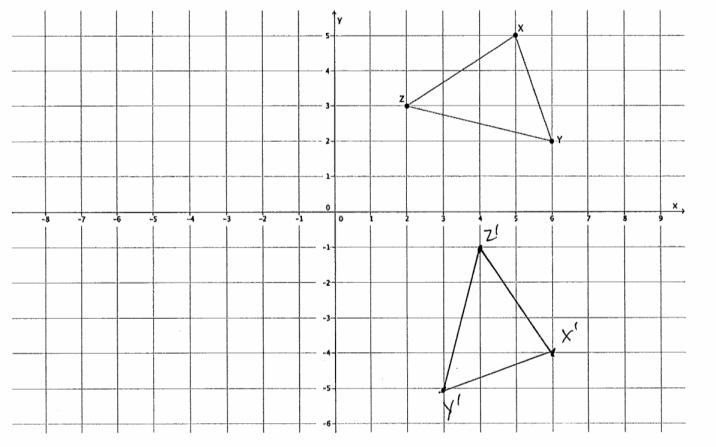
Use the picture below to answer the questions.
Answer:
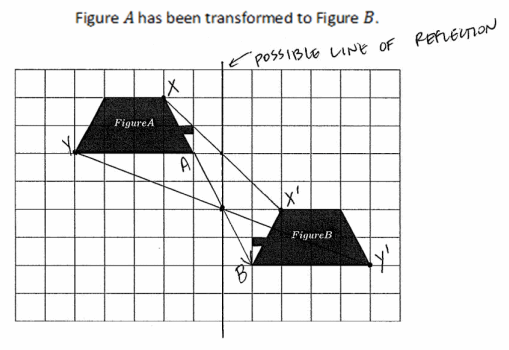
a. Can Figure A be mapped onto Figure B using only translation? Explain. Use drawings as needed in your explanation.
Answer:
No, if i translate along vector \(\overrightarrow{A B}\) i can get the longer point of figure A to map onto the lower left point of figure B(one pair of corresponding points). But no other points of the figures coincide.)
b. Can Figure A be mapped onto Figure B using only reflection? Explain. Use drawings as needed in your explanation. Use the graphs below to answer parts (a) and (b).
Answer:
No, when i connect a point of figure A to its image on figure B, the line of reflection should bisect the segment. When i connect midpoints of \(\overline{x x^{\prime}}\) & \(\overline{y y^{\prime}}\) i get a possible line of reflection, but when i check, figure A does not map onto figure B.
Question 3.
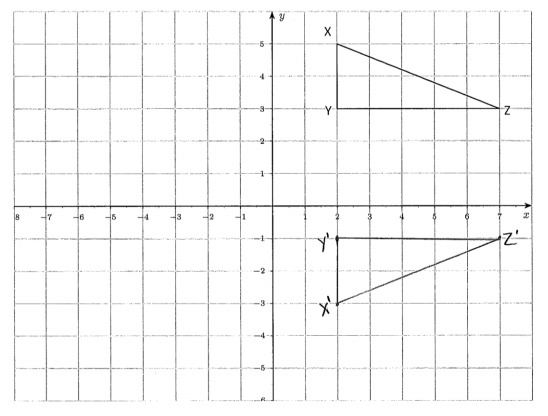
Reflect △XYZ over the horizontal line (parallel to the x-axis) through point (0,1). Label the reflected image with X’Y’Z’.
a. Reflect △XYZ over the horizontal line (parallel to the x-axis) through point (0,1). Label the reflected image with X’Y’Z’.
Answer:
b. One triangle in the diagram below can be mapped onto the other using two reflections. Identify the lines of reflection that would map one onto the other. Can you map one triangle onto the other using just one basic rigid motion? If so, explain.
Answer:
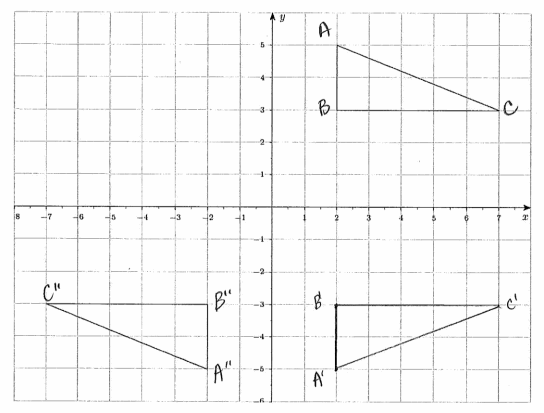
A reflection across the x-axis maps △ABC to △A’B’C’ and a reflection across the y-axis maps △A’B’C’ to △A”B”C”.
Since AB || A”B”, BC = B”C”, AC = A”C”, then A 180° rotation about the origin will map △ABC to △A”B”C”.