Engage NY Eureka Math 8th Grade Module 2 Lesson 4 Answer Key
Eureka Math Grade 8 Module 2 Lesson 4 Exercise Answer Key
Exercise 1.
Reflect △ABC and Figure D across line L. Label the reflected images.
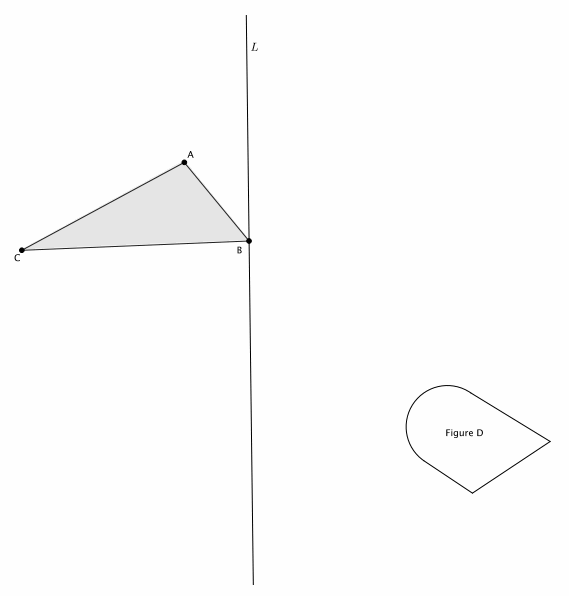
Answer:
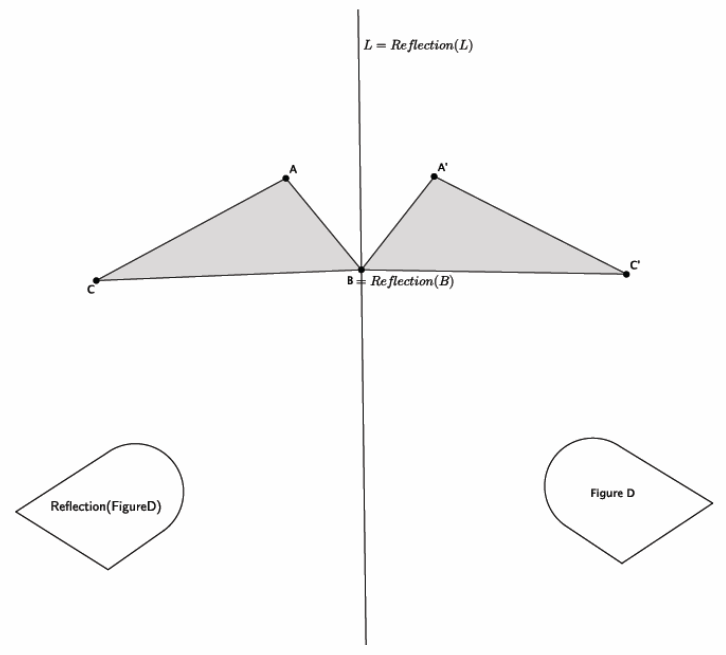
Exercise 2.
Which figure(s) were not moved to a new location on the plane under this transformation?
Answer:
Point B and line L were not moved to a new location on the plane under this reflection.
Exercises 3–5
Exercise 3.
Reflect the images across line L. Label the reflected images.
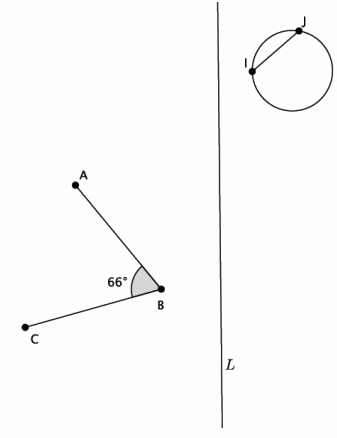
Answer:
Exercise 4.
Answer the questions about the image above.
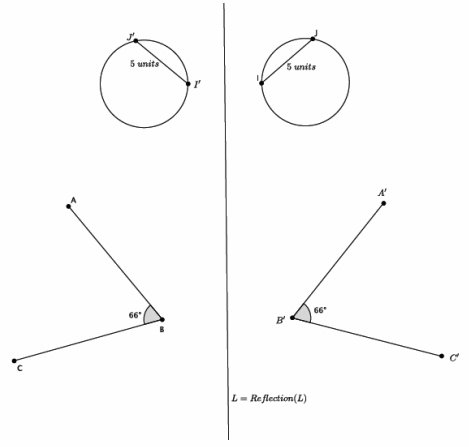
a. Use a protractor to measure the reflected ∠ABC. What do you notice?
Answer:
The measure of the reflected image of ∠ABC is 66°.
b. Use a ruler to measure the length of IJ and the length of the image of IJ after the reflection. What do you notice?
Answer:
The length of the reflected segment is the same as the original segment, 5 units.
Note: This is not something students are expected to know, but it is a preview for what is to come later in this lesson.
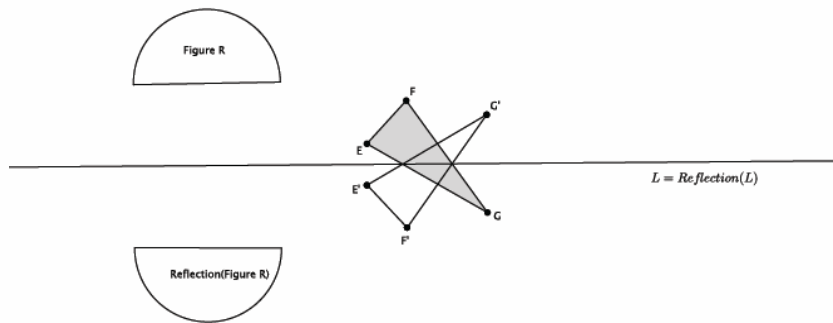
Exercise 5.
Reflect Figure R and △EFG across line L. Label the reflected images.
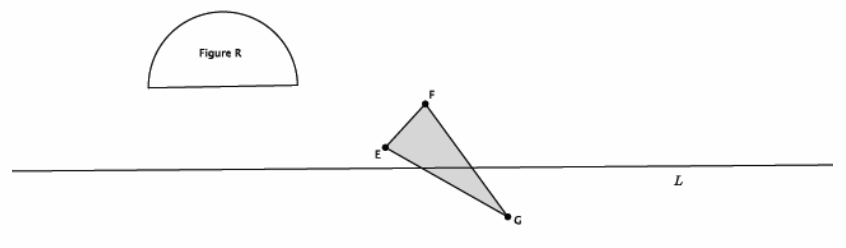
Answer:
Exercises 6–9
Use the picture below for Exercises 6–9.
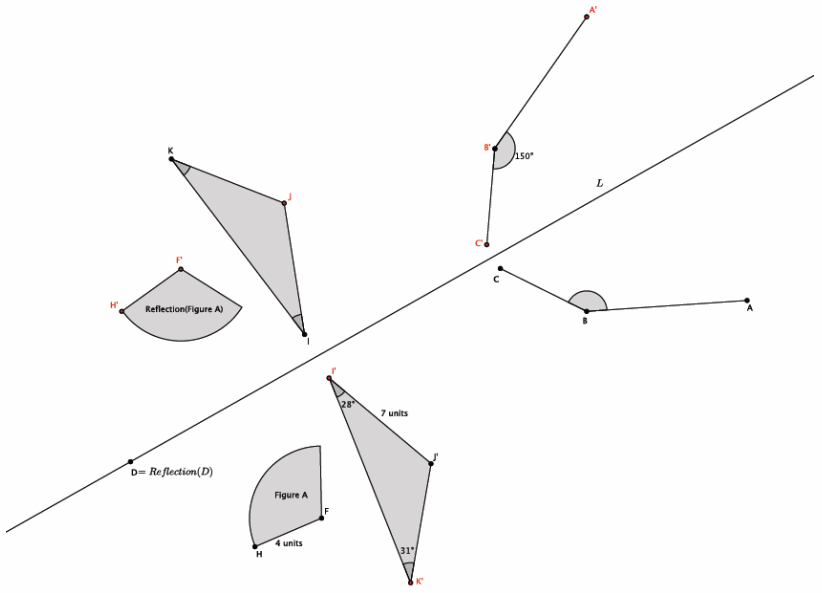
Exercise 6.
Use the picture to label the unnamed points.
Answer:
Points are labeled in red above.
Exercise 7.
What is the measure of ∠JKI? ∠KIJ? ∠ABC? How do you know?
Answer:
m∠JKI=31°, m∠KIJ=28°, and m∠ABC=150°. Reflections preserve angle measures.
Exercise 8.
What is the length of segment Reflection(FH)? IJ? How do you know?
Answer:
|Reflection(FH)|=4 units, and IJ=7 units. Reflections preserve lengths of segments.
Exercise 9.
What is the location of Reflection(D)? Explain.
Answer:
Point D and its image are in the same location on the plane. Point D was not moved to another part of the plane because it is on the line of reflection. The image of any point on the line of reflection will remain in the same location as the original point.
Eureka Math Grade 8 Module 2 Lesson 4 Exit Ticket Answer Key
Question 1.
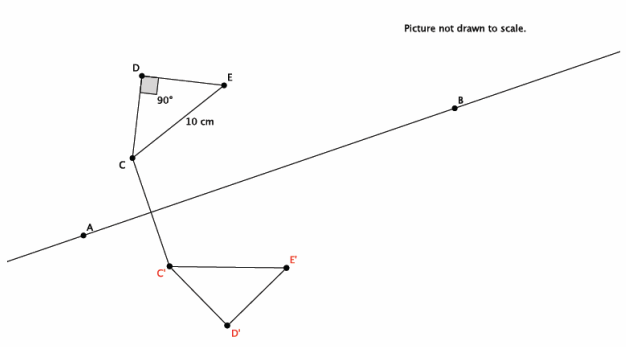
Let there be a reflection across line LAB. Reflect △CDE across line LAB. Label the reflected image.
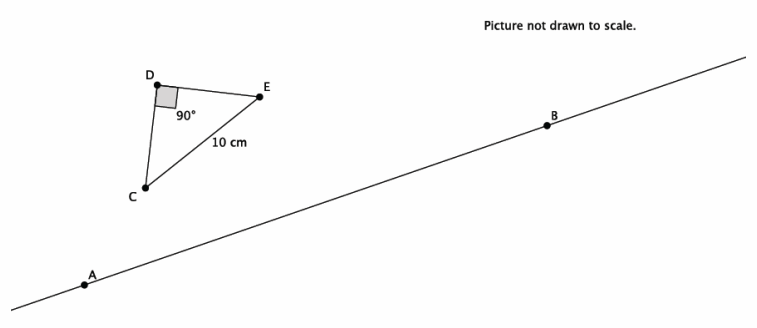
Answer:
Question 2.
Use the diagram above to state the measure of Reflection(∠CDE). Explain.
Answer:
The measure of Reflection(∠CDE) is 90° because reflections preserve degrees of measures of angles.
Question 3.
Use the diagram above to state the length of segment Reflection(CE). Explain.
Answer:
The length of Reflection(CE) is 10 cm because reflections preserve segment lengths.
Question 4.
Connect point C to its image in the diagram above. What is the relationship between line LAB and the segment that connects point C to its image?
Answer:
The line of reflection bisects the segment that connects C to its image.
Eureka Math Grade 8 Module 2 Lesson 4 Problem Set Answer Key
Question 1.
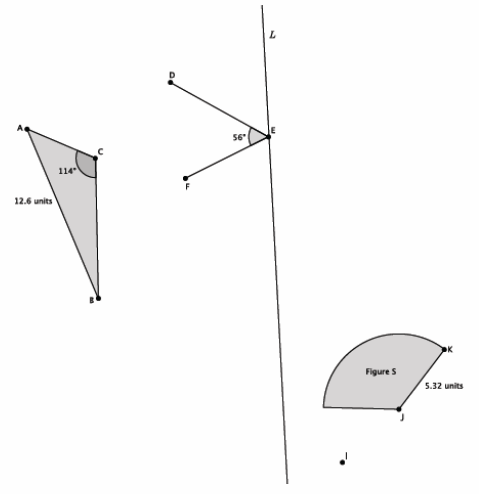
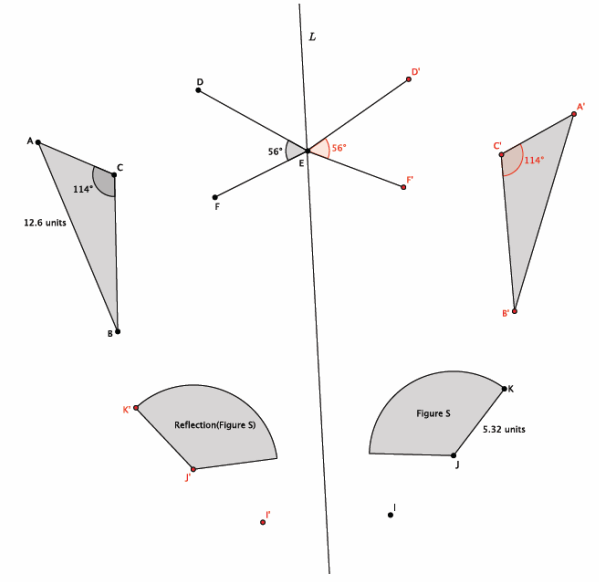
In the picture below, ∠DEF=56°, ∠ACB=114°, AB=12.6 units, JK=5.32 units, point E is on line L, and point I is off of line L. Let there be a reflection across line L. Reflect and label each of the figures, and answer the questions that follow.
Answer:
Question 2.
What is the measure of Reflection(∠DEF)? Explain.
Answer:
The measure of Reflection(∠DEF) is 56°. Reflections preserve degrees of angles.
Question 3.
What is the length of Reflection(JK)? Explain.
Answer:
The length of Reflection(JK) is 5.32 units. Reflections preserve lengths of segments.
Question 4.
What is the measure of Reflection(∠ACB)?
Answer:
The measure of Reflection(∠ACB) is 114°.
Question 5.
What is the length of Reflection(AB)?
Answer:
The length of Reflection(AB) is 12.6 units.
Question 6.
Two figures in the picture were not moved under the reflection. Name the two figures, and explain why they were not moved.
Answer:
Point E and line L were not moved. All of the points that make up the line of reflection remain in the same location when reflected. Since point E is on the line of reflection, it is not moved.
Question 7.
Connect points I and I’. Name the point of intersection of the segment with the line of reflection point Q. What do you know about the lengths of segments IQ and QI’?
Answer:
Segments IQ and QI’ are equal in length. The segment II’ connects point I to its image, I’. The line of reflection will go through the midpoint, or bisect, the segment created when you connect a point to its image.