Engage NY Eureka Math 8th Grade Module 2 Lesson 2 Answer Key
Eureka Math Grade 8 Module 2 Lesson 2 Exercise Answer Key
Exercise 1.
Draw at least three different vectors, and show what a translation of the plane along each vector looks like. Describe what happens to the following figures under each translation using appropriate vocabulary and notation as needed.
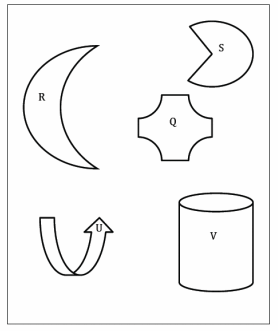
Answer:
Answers will vary.
Exercise 2.
The diagram below shows figures and their images under a translation along \(\overrightarrow{H I}\). Use the original figures and the translated images to fill in missing labels for points and measures.
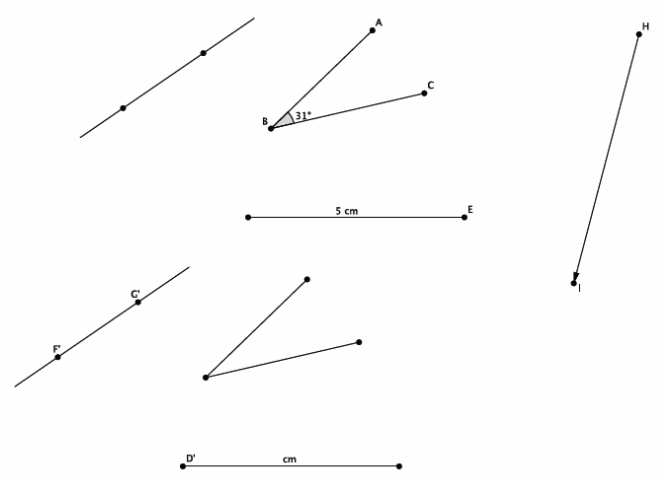
Answer:
Solutions are in red, below.
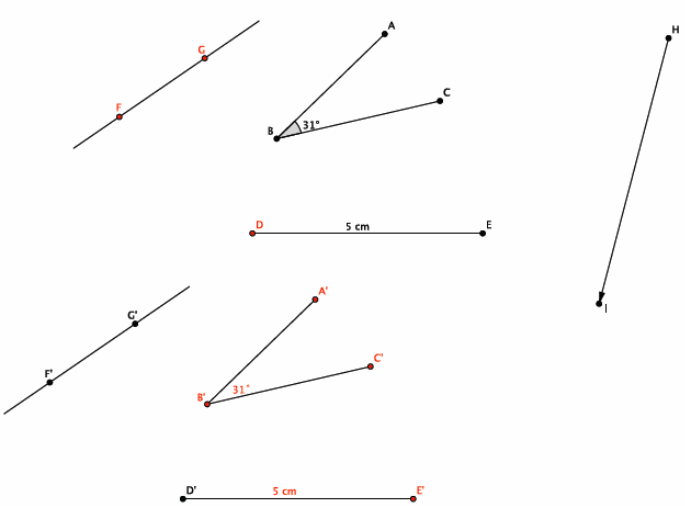
Eureka Math Grade 8 Module 2 Lesson 2 Exit Ticket Answer Key
Question 1.
Name the vector in the picture below.

Answer:
\(\overrightarrow{Q P}\)
Question 2.
Name the vector along which a translation of a plane would map point A to its image T(A).
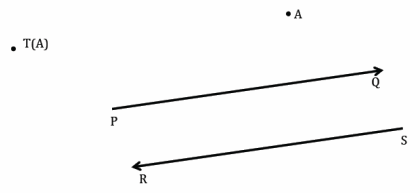
Answer:
\(\overrightarrow{S R}\)
Question 3.
Is Maria correct when she says that there is a translation along a vector that maps segment AB to segment CD? If so, draw the vector. If not, explain why not.
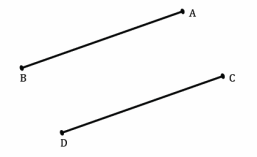
Answer:
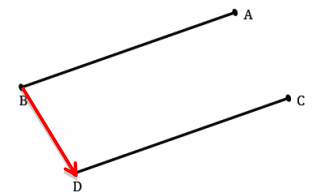
Yes. Accept any vector that would translate the segment AB to segment CD. A possible vector is shown in red, above.
Question 4.
Assume there is a translation that maps segment AB to segment CD shown above. If the length of segment CD is 8 units, what is the length of segment AB? How do you know?
Answer:
The length of CD must be 8 units in length because translations preserve the lengths of segments.
Eureka Math Grade 8 Module 2 Lesson 2 Problem Set Answer Key
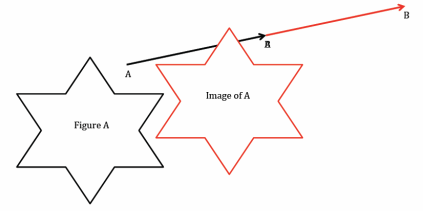
Question 1.
Translate the plane containing Figure A along \(\overrightarrow{A B}\). Use your transparency to sketch the image of Figure A by this translation. Mark points on Figure A, and label the image of Figure A accordingly.
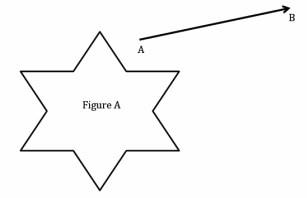
Answer:
Marked points will vary. Verify that students have labeled their points and images appropriately.
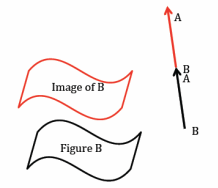
Question 2.
Translate the plane containing Figure B along \(\overrightarrow{B A}\). Use your transparency to sketch the image of Figure B by this translation. Mark points on Figure B, and label the image of Figure B accordingly.
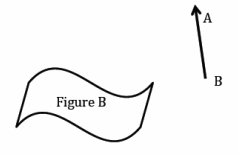
Answer:
Marked points will vary. Verify that students have labeled their points and images appropriately.
Question 3.
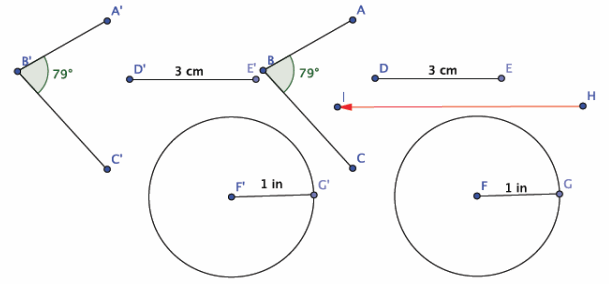
Draw an acute angle (your choice of degree), a segment with length 3 cm, a point, a circle with radius 1 in., and a vector (your choice of length, i.e., starting point and ending point). Label points and measures (measurements do not need to be precise, but your figure must be labeled correctly). Use your transparency to translate all of the figures you have drawn along the vector. Sketch the images of the translated figures and label them.
Answer:
Drawings will vary. Note: Drawing is not to scale.
Question 4.
What is the length of the translated segment? How does this length compare to the length of the original segment? Explain.
Answer:
The length is 3 cm. The length is the same as the original because translations preserve the lengths of segments.
Question 5.
What is the length of the radius in the translated circle? How does this radius length compare to the radius of the original circle? Explain.
Answer:
The length is 1 in. The length is the same as the original because translations preserve lengths of segments.
Question 6.
What is the degree of the translated angle? How does this degree compare to the degree of the original angle? Explain.
Answer:
Answers will vary based on the original size of the angle drawn. The angles will have the same measure because translations preserve degrees of angles.
Question 7.
Translate point D along vector \(\overrightarrow{A B}\), and label the image D’. What do you notice about the line containing vector \(\overrightarrow{A B}\) and the line containing points D and D’? (Hint: Will the lines ever intersect?)
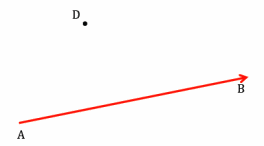
Answer:
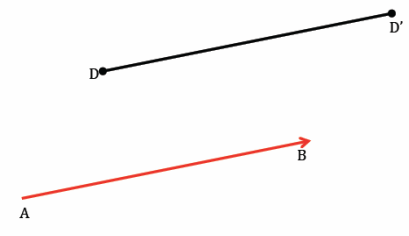
The lines will be parallel.
Question 8.
Translate point E along vector \(\overrightarrow{A B}\), and label the image E’. What do you notice about the line containing vector \(\overrightarrow{A B}\) and the line containing points E and E’?
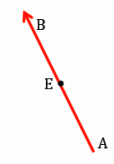
Answer:
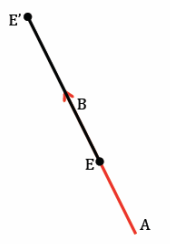
The lines will coincide.