Engage NY Eureka Math 8th Grade Module 1 Mid Module Assessment Answer Key
Eureka Math Grade 8 Module 1 Mid Module Assessment Task Answer Key
Question 1.
The number of users of social media has increased significantly since the year 2001. In fact, the approximate number of users has tripled each year. It was reported that in 2005 there were 3 million users of social media.
a. Assuming that the number of users continues to triple each year, for the next three years, determine the number of users in 2006, 2007, and 2008.
Answer:
2006-9 MILLION
2007-27 MILLION
2008-81 MILLION
b. Assume the trend in the numbers of users tripling each year was true for all years from 2001 to 2009. Complete the table below using 2005 as year 1 with 3 million as the number of users that year.

Answer:

c. Given only the number of users in 2005 and the assumption that the number of users triples each year, how did you determine the number of users for years 2, 3, 4, and 5?
Answer:
I MULTIPLIED THE PRECEDING YEAR’S NUMBER OF USERS BY 3.
d. Given only the number of users in 2005 and the assumption that the number of users triples each year, how did you determine the number of users for years 0, -1, -2, and -3?
Answer:
I Divided The Next Year’s Number of users by 3.
e. Write an equation to represent the number of users in millions, N, for year t, t≥-3.
Answer:
N=3t
f. Using the context of the problem, explain whether or not the formula N=3t would work for finding the number of users in millions in year t, for all t≤0.
Answer:
We only know that the number of users has tripled each year in the time frame of 2001 to 2009. For that reason, we cannot rely on the formula, N = 3t, to work for all t≤0, just to t=-3, which is the year 2001.
g. Assume the total number of users continues to triple each year after 2009. Determine the number of users in 2012. Given that the world population at the end of 2011 was approximately 7 billion, is this assumption reasonable? Explain your reasoning.
Answer:
2012 is t=8, so when t=8 in N=6,561,000,000. The number of users in 2012, 6,561,000,000. Does not exceed the world population of 7 billion, therefore it is possible to have that number of users. But 6,561,000,000 is Approximately 94%. of the world’s population. The number of users is likely less than that due to poverty, illness, infancy, etc. The Assumption is possible, but not reasonable.
Question 2.
Let m be a whole number.
a. Use the properties of exponents to write an equivalent expression that is a product of unique primes, each raised to an integer power.
\(\frac{6^{21} \cdot 10^{7}}{30^{7}}\)
Answer:
\(\frac{(3 \cdot 2)^{21} \cdot 10^{7}}{(3 \cdot 10)^{7}}\)=\(\frac{3^{21} \cdot 2^{21} \cdot 10^{7}}{3^{7} \cdot 10^{7}}\)
= 321-7.221.107-7
= 314.221.100
= 314.221
b. Use the properties of exponents to prove the following identity:
\(\frac{6^{3 m} \cdot 10^{m}}{30^{m}}\) = 23m.32m
Answer:
\(\frac{6^{3 m} \cdot 10^{m}}{30^{m}}\) = \(\frac{(3.2)^{3 m} \cdot 10^{m}}{(3 \cdot 10)^{m}}\)
= \(\frac{3^{3 m} \cdot 2^{3 m} \cdot 10^{m}}{3^{m} \cdot 10^{m}}\)
= 33m-3.23m.10m-m
= 32m.23m
= 23m.32m
c. What value of m could be substituted into the identity in part (b) to find the answer to part (a)?
Answer:
23m.32m = 221.314
3m = 21
m = 7
2m = 14
m = 7
Therefore, m = 7
Question 3.
Jill writes 23 ∙43 =86 and the teacher marked it wrong. Explain Jill’s error.
Answer:
Jill multiplied the bases, 2 and 4, and added the exponents. You can only add the exponents when the bases being multiplied are the same.
b. Find n so that the number sentence below is true:
23 ∙43 =23 ∙2n =29
Answer:
43 = 4.4.4
= (2.2)(2.2)(2.2)
= 26
Therefore
23.43 = 23.26 = 29
so
n = 6
c. Use the definition of exponential notation to demonstrate why 23 ∙43 =29 is true.
Answer:
43=26, 23.43 = 29 is equivalent to 23.26 = 29
By definition of exponential notation:
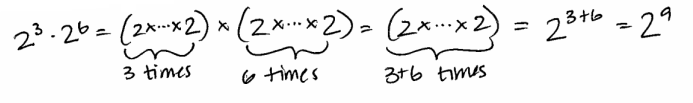
d. You write 75 ∙7-9 =7-4 . Keisha challenges you, “Prove it!” Show directly why your answer is correct without referencing the laws of exponents for integers; in other words, xa ∙xb =xa+b for positive numbers x and integers a and b.
Answer:
75.7-9 = 75.\(\frac{1}{7^{9}}\) by definition
= \(\frac{7^{5}}{7^{9}}\) by product formula
= \(\frac{7^{5}}{7^{5.7^{4}}}\) by xm.xn = xm+n for x>0, m,n≥0
= \(\frac{1}{7^{4}}\) by equivalent fractions
= 7-4 by definition.