Engage NY Eureka Math 8th Grade Module 1 Lesson 2 Answer Key
Eureka Math Grade 8 Module 1 Lesson 2 Example Answer Key
Examples 1–2
Work through Examples 1 and 2 in the manner just shown. (Supplement with additional examples if needed.)
It is preferable to write the answers as an addition of exponents to emphasize the use of the identity. That step should not be left out. That is, 52×54=56 does not have the same instructional value as 52×54=52+4.
Example 1.
52×54=
Answer:
52+4
Example 2.
(-\(\frac{2}{3}\))4×(-\(\frac{2}{3}\))5=(-\(\frac{2}{3}\))4+5
→ What is the analog of xm∙xn=xm+n in the context of repeated addition of a number x?
Allow time for a brief discussion.
→ If we add m copies of x and then add to it another n copies of x, we end up adding m+n copies of x. By the distributive law:
mx+nx=(m+n)x .
This is further confirmation of what we observed at the beginning of Lesson 1: The exponent m+n in xm+n in the context of repeated multiplication corresponds exactly to the m+n in (m+n)x in the context of repeated addition.
Examples 3–4.
Work through Examples 3 and 4 in the manner shown. (Supplement with additional examples if needed.)
It is preferable to write the answers as a subtraction of exponents to emphasize the use of the identity.
Example 3.
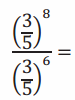
Answer:
(\(\frac{3}{5}\))8-6
Example 4.
\(\frac{4^{5}}{4^{2}}\) =
Answer:
45-2
Eureka Math Grade 8 Module 1 Lesson 2 Exercise Answer Key
Exercise 1.
1423×148=
Answer:
1423+8
Exercise 2.
(-72)10×(-72)13=
Answer:
(-72)10+13
Exercise 3.
594×578=
Answer:
594+78
Exercise 4.
(-3)9×(-3)5=
Answer:
(-3)9+5
Exercise 5.
Let a be a number.
a23∙a8=
Answer:
a23+8
Exercise 6.
Let f be a number.
f10∙f13=
Answer:
f10+13
Exercise 7.
Let b be a number.
b94∙b78=
Answer:
b94+78
Exercise 8.
Let x be a positive integer. If (-3)9×(-3)x=(-3)14, what is x?
Answer:
x=5
In Exercises 9–16, students need to think about how to rewrite some factors so the bases are the same. Specifically, 24×82=24×26=24+6 and 37×9=37×32=37+2. Make clear that these expressions can only be combined into a single base because the bases are the same. Also included is a non-example, 54×211, that cannot be combined into a single base using this identity. Exercises 17–20 offer further applications of the identity.
What would happen if there were more terms with the same base? Write an equivalent expression for each problem.
Exercise 9.
94×96×913=
Answer:
94+6+13
Exercise 10.
23×25×27×29=
Answer:
23+5+7+9
Can the following expressions be written in simpler form? If so, write an equivalent expression. If not, explain why not.
Exercise 11.
65×49×43×614=
Answer:
49+3×65+14
Exercise 12.
(-4)2∙175∙(-4)3∙177=
Answer:
(-4)2+3∙175+7
Exercise 13.
152∙72∙15∙74=
Answer:
152+1∙72+4
Exercise 14.
24×82=24×26=
Answer:
24+6
Exercise 15.
37×9=37×32=
Answer:
37+2
Exercise 16.
54 ×211=
Answer:
Cannot be simplified. Bases are different and cannot be rewritten in the same base.
Exercise 17.
Let x be a number. Rewrite the expression in a simpler form.
(2x3 )(17x7 )=
Answer:
34x10
Exercise 18.
Let a and b be numbers. Use the distributive law to rewrite the expression in a simpler form.
a(a+b)=
Answer:
a2+ab
Exercise 19.
Let a and b be numbers. Use the distributive law to rewrite the expression in a simpler form.
b(a+b)=
Answer:
ab+b2
Exercise 20.
Let a and b be numbers. Use the distributive law to rewrite the expression in a simpler form.
(a+b)(a+b)=
Answer:
a2+ab+ba+b2=a2+2ab+b2
Exercise 21.
\(\frac{7^{9}}{7^{6}}\) =
Answer:
79-6
Exercise 22.
\(\frac{(-5)^{16}}{(-5)^{7}}\) =
Answer:
(-5)16-7
Exercise 23.
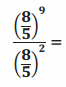
Answer:
(\(\frac{8}{5}\))9-2
Exercise 24.
\(\frac{13^{5}}{13^{4}}\)=
Answer:
135-4
Exercise 25.
Let a, b be nonzero numbers. What is the following number?
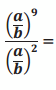
Answer:
(\(\frac{a}{b}\))9-2
Exercise 26.
Let x be a nonzero number. What is the following number?
\(\frac{x^{5}}{x^{4}}\) =
Answer:
x5-4
Can the following expressions be written in simpler forms? If yes, write an equivalent expression for each problem. If not, explain why not.
Exercise 27.
\(\frac{2^{7}}{4^{2}}\) = \(\frac{2^{7}}{2^{4}}\) =
Answer:
27-4
Exercise 28.
\(\frac{3^{23}}{27}\)= \(\frac{3^{23}}{3^{3}}\) =
Answer:
323-3
Exercise 29.
\(\frac{3^{5} \cdot 2^{8}}{3^{2} \cdot 2^{3}}\)=
Answer:
35-2∙28-3
Exercise 30.
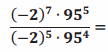
Answer:
(-2)7-5∙955-4
Exercise 31.
Let x be a number. Write each expression in a simpler form.
a. \(\frac{5}{x^{3}}\)(3x8 )=
Answer:
15x5
b. \(\frac{5}{x^{3}}\)(-4x6 )=
Answer:
-20x3
c. \(\frac{5}{x^{3}}\)(11x4 )=
Answer:
55x
Exercise 32.
Anne used an online calculator to multiply 2 000 000 000×2 000 000 000 000. The answer showed up on the calculator as 4e+21, as shown below. Is the answer on the calculator correct? How do you know?
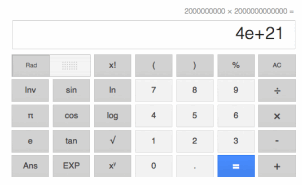
Answer:
2 000 000 000×2 000 000 000 000=4 000 000 000 000 000 000 000.
The answer must mean 4 followed by 21 zeros. That means that the answer on the calculator is correct.
This problem is hinting at scientific notation (i.e., (2× 109)(2×1012)=4×109+12). Accept any reasonable explanation of the answer.
Eureka Math Grade 8 Module 1 Lesson 2 Problem Set Answer Key
To ensure success with Problems 1 and 2, students should complete at least bounces 1–4 with support in class. Consider working on Problem 1 as a class activity and assigning Problem 2 for homework.
Students may benefit from a simple drawing of the scenario. It will help them see why the factor of 2 is necessary when calculating the distance traveled for each bounce. Make sure to leave the total distance traveled in the format shown so that students can see the pattern that is developing. Simplifying at any step will make it difficult to write the general statement for n number of bounces.
Question 1.
A certain ball is dropped from a height of x feet. It always bounces up to \(\frac{2}{3}\) x feet. Suppose the ball is dropped from 10 feet and is stopped exactly when it touches the ground after the 30th bounce. What is the total distance traveled by the ball? Express your answer in exponential notation.
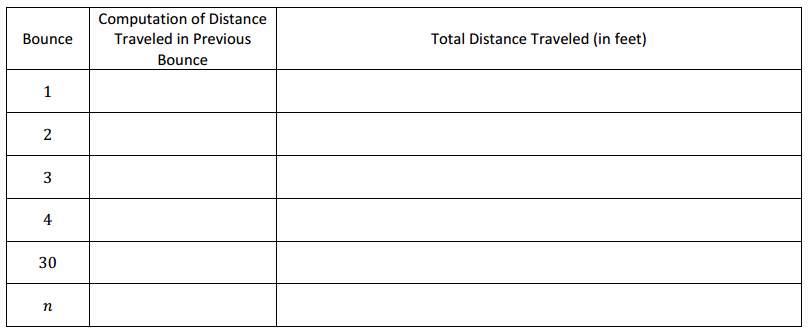
Answer:

Question 2.
If the same ball is dropped from 10 feet and is stopped exactly at the highest point after the 25th bounce, what is the total distance traveled by the ball? Use what you learned from the last problem.
Answer:
Based on the last problem, we know that each bounce causes the ball to travel 2(\(\frac{2}{3}\))n 10 feet. If the ball is stopped at the highest point of the 25th bounce, then the distance traveled on that last bounce is just (\(\frac{2}{3}\))25 10 feet because it does not make the return trip to the ground. Therefore, the total distance traveled by the ball in feet in this situation is
10+2(\(\frac{2}{3}\))10+2(\(\frac{2}{3}\))2 10+2(\(\frac{2}{3}\))3 10+2(\(\frac{2}{3}\))4 10+…..+2(\(\frac{2}{3}\))2310+2(\(\frac{2}{3}\))2410.
Question 3.
Let a and b be numbers and b≠0, and let m and n be positive integers. Write each expression using the fewest number of bases possible.
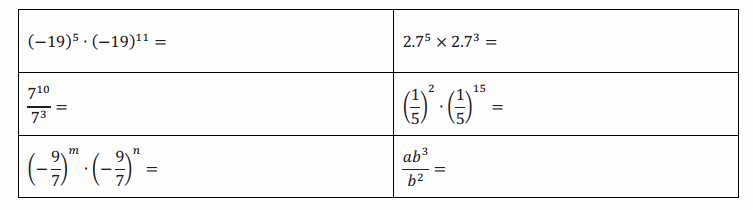
Answer:
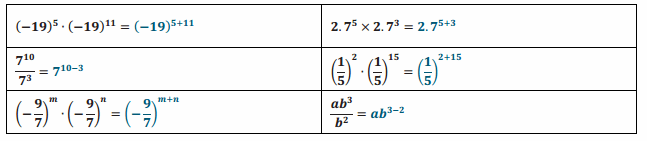
Question 4.
Let the dimensions of a rectangle be (4×(871209)5+ 3×49 762 105) ft. by (7×(871 209)3-(49 762 105)4) ft. Determine the area of the rectangle. (Hint: You do not need to expand all the powers.)
Answer:
Area=(4×(871 209)5+3×49 762 105) ft.(7×(871 209)3-(49 762 105)4 ) ft.
=(28×(871 209)8-4×(871 209)5 (49 762 105)4+21×(871 209)3 (49 762 105)-3×(49 762 105)5 ) sq.ft.
Question 5.
A rectangular area of land is being sold off in smaller pieces. The total area of the land is 215 square miles. The pieces being sold are 83 square miles in size. How many smaller pieces of land can be sold at the stated size? Compute the actual number of pieces.
Answer:
83=29
\(\frac{2^{15}}{2^{9}}\) =215-9=26=64
64 pieces of land can be sold.
Eureka Math Grade 8 Module 1 Lesson 2 Exit Ticket Answer Key
Note to Teacher: Accept both forms of the answer; in other words, accept an answer that shows the exponents as a sum or difference as well as an answer where the numbers are actually added or subtracted.
Write each expression using the fewest number of bases possible.
Question 1.
Let a and b be positive integers. 23a × 23b=
Answer:
23a × 23b = 23a+b
Question 2.
53×25=
Answer:
53×25=53×52
= 53+2
=55
Question 3.
Let x and y be positive integers and x>y. \(\frac{11^{x}}{11^{y}}\) =
Answer:
\(\frac{11^{x}}{11^{y}}\) = 11x-y
Question 4.
\(\frac{2^{13}}{8}\) =
Answer:
\(\frac{2^{13}}{2^{3}}\) = 213-3 = 210