Engage NY Eureka Math 8th Grade Module 1 Lesson 12 Answer Key
Eureka Math Grade 8 Module 1 Lesson 12 Exercise Answer Key
Exercise 1.
A certain brand of MP3 player will display how long it will take to play through its entire music library. If the maximum number of songs the MP3 player can hold is 1,000 (and the average song length is 4 minutes), would you want the time displayed in terms of seconds-, days-, or years-worth of music? Explain.
Answer:
It makes the most sense to have the time displayed in days because numbers such as 240,000 seconds-worth of music and \(\frac{5}{657}\) of a year are more difficult to understand than about 2.8 days.
Exercise 2.
You have been asked to make frosted cupcakes to sell at a school fundraiser. Each frosted cupcake contains about 20 grams of sugar. Bake sale coordinators expect 500 people will attend the event. Assume everyone who attends will buy a cupcake; does it make sense to buy sugar in grams, pounds, or tons? Explain.
Answer:
Because each cupcake contains about 20 grams of sugar, we will need 500×20 grams of sugar. Therefore, grams are too small of a measurement, while tons are too large. Therefore, the sugar should be purchased in pounds.
Exercise 3.
The seafloor spreads at a rate of approximately 10 cm per year. If you were to collect data on the spread of the seafloor each week, which unit should you use to record your data? Explain.
Answer:
The seafloor spreads 10 cm per year, which is less than 1 cm per month. Data will be collected each week, so it makes the most sense to measure the spread with a unit like millimeters.
Exercise 4.
Show that the mass of a proton is 0.938 \(\frac{\mathrm{GeV}}{c^{2}}\).
Answer:
Let x represent the number of gigaelectronvolts equal to the mass of a proton.
x(\(\frac{\mathrm{GeV}}{c^{2}}\))=mass of proton
x(1.783×10-27)=1.672622×10-27
x=(1.672622×10-27)/(1.783×10-27)
=\(\frac{1.672622}{1.783}\)
≈0.938
Exercise 5.
The distance of the nearest star (Proxima Centauri) to the sun is approximately 4.013 336 473×1013 km. Show that Proxima Centauri is 4.2421 light-years from the sun.
Answer:
Let x represent the number of light-years Proxima Centauri is from the sun.
x(9.46073×1012)=4.013336473×1013
x=\(\frac{4.013336473 \times 10^{13}}{9.46073 \times 10^{12}}\)
=\(\frac{4.013336473}{9.46073}\)×10
=0.424210021×10
≈4.2421
Exercise 6.
What new unit might you introduce in order to discuss the differences in diameter measurements?
Answer:
There are several answers that students could give for their choice of unit. Accept any reasonable answer, provided the explanation is clear and correct. Some students may choose 10-12 as their unit because all measurements could then be expressed without exponential notation. Other students may decide that 10-8 should be the unit because two measurements are already of that order of magnitude. Still, other students may choose 10-10 because that is the average of the powers.
Exercise 7.
Name your unit, and explain why you chose it.
Answer:
Students can name their unit anything reasonable, as long as they clearly state what their unit is and how it will be written. For example, if a student chooses a unit of 10-10, then he or she should state that the unit will be represented with a letter. For example, Y, then Y=10-10.
Exercise 8.
Using the unit you have defined, rewrite the five diameter measurements.
Answer:
Using the unit Y=10-10, then:
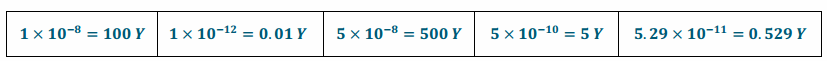
Eureka Math Grade 8 Module 1 Lesson 12 Exploratory Challenge Answer Key
Exploratory Challenge 1.
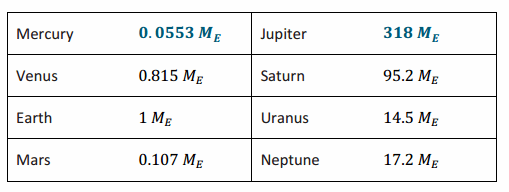
Finally, let us look at an example involving the masses of the planets in our solar system. They range from Mercury’s 3.3022×1023 kg to Jupiter’s 1.8986×1027 kg. However, Earth’s mass is the fourth heaviest among the eight planets3, and it seems reasonable to use it as the point of reference for discussions among planets. Therefore, a new unit is ME, the mass of the Earth, or 5.97219×1024 kg.
Suggested white-board activity: Show students the table below, leaving the masses for Mercury and Jupiter blank. Demonstrate how to rewrite the mass of Mercury in terms of the new unit, ME. Then, have students rewrite the mass of Jupiter using the new unit. Finally, complete the chart with the rewritten masses.
Mercury: Let x represent the mass of Mercury in the unit ME. We want to determine what number times the new unit is equal to the mass of Mercury in kilograms. Since ME=5.97219×1024, then:
(5.97219×1024 )x=3.3022×1023
x=\(\frac{3.3022 \times 10^{23}}{5.97219 \times 10^{24}}\)
= \(\frac{3.3022}{5.97219}\) × \(\frac{10^{23}}{10^{24}}\)
≈0.553×101-
=0.0553.
Mercury’s mass is 0.0553 ME.
Jupiter: Let x represent the mass of Jupiter in the unit ME. We want to determine what number times the new unit is equal to the mass of Jupiter in kilograms. Since ME=5.97219×1024, then:
(5.97219×1024 )x=1.8986×1027
x=\(\frac{1.8986 \times 10^{27}}{5.97219 \times 10^{24}}\)
=\(\frac{1.8986}{5.97219}\)×\(\frac{10^{27}}{10^{24}}\)
≈0.318×103
=318.
Jupiter’s mass is 318 ME.
Exploratory Challenge 2.
Suppose you are researching atomic diameters and find that credible sources provided the diameters of five different atoms as shown in the table below. All measurements are in centimeters.
Eureka Math Grade 8 Module 1 Lesson 12 Exit Ticket Answer Key
Question 1.
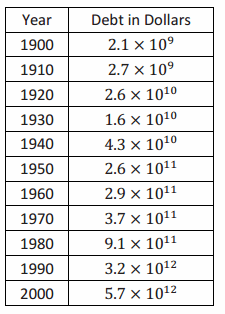
The table below shows an approximation of the national debt at the beginning of each decade over the last century. Choose a unit that would make a discussion about the growth of the national debt easier. Name your unit, and explain your choice.
Answer:
Students will likely choose 1011 as their unit because the majority of the data is of that magnitude. Accept any reasonable answer that students provide. Verify that they have named their unit.
Question 2.
Using the new unit you have defined, rewrite the debt for years 1900, 1930, 1960, and 2000.
Answer:
Let D represent the unit 1011. Then, the debt in 1900 is 0.021D, in 1930 it is 0.16D, in 1960 it is 2.9D, and 57D in 2000.
Eureka Math Grade 8 Module 1 Lesson 12 Problem Set Answer Key
Question 1.
Verify the claim that, in terms of gigaelectronvolts, the mass of an electron is 0.000511.
Answer:
Let x represent the number of gigaelectronvolts equal to the mass of an electron.
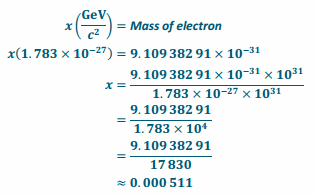
Question 2.
The maximum distance between Earth and the sun is 1.52098232×108 km, and the minimum distance is 1.47098290×108 km. What is the average distance between Earth and the sun in scientific notation?
Answer:
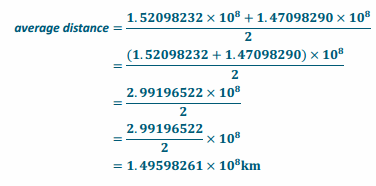
Question 3.
Suppose you measure the following masses in terms of kilograms:
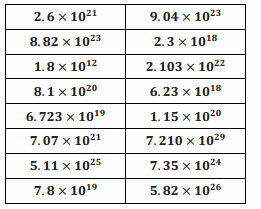
What new unit might you introduce in order to aid discussion of the masses in this problem? Name your unit, and express it using some power of 10. Rewrite each number using your newly defined unit.
Answer:
A very motivated student may search the Internet and find that units exist that convert large masses to reasonable numbers, such as petagrams (1012 kg), exagrams (1015 kg), or zetagrams (1018 kg). More likely, students will decide that something near 1020 should be used as a unit because many of the numbers are near that magnitude. There is one value, 1.8×1012, that serves as an outlier and should be ignored because it is much smaller than the majority of the data. Students can name their unit anything reasonable. The answers provided are suggestions, but any reasonable answers should be accepted.
Let U be defined as the unit 1020.
