Engage NY Eureka Math 7th Grade Module 6 Mid Module Assessment Answer Key
Eureka Math Grade 7 Module 6 Mid Module Assessment Task Answer Key
Question 1.
In each problem, set up and solve an equation for the unknown angles.
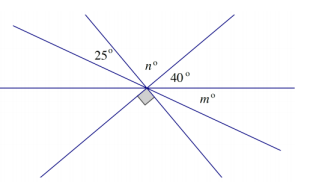
a. Four lines meet at a point. Find the measures m° and n°.
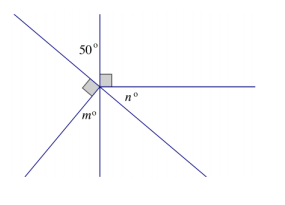
b. Two lines meet at the vertex of two rays. Find the measures m° and n°.
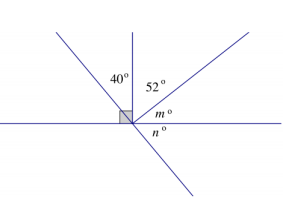
c. Two lines meet at a point that is the vertex of two rays. Find the measures m° and n°.
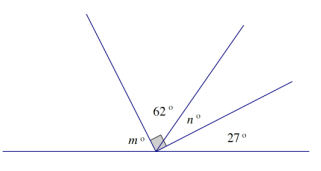
d. Three rays have a common vertex on a line. Find the measures m° and n°.
Answer:
a. n° = 90° , vertical angles
25° + (90°) + 40° + m° = 180°
155° + m° = 180°
155° – 155° + m° = 180° – 155°
m° = 25°
b. 50° + 90° + n° = 180°
140° + n° = 180°
140° – 140° + n° = 180° – 140°
n° = 40°
m° + 50° = 90°
m° + 50° – 50° = 90° – 50°
m° = 40°
c. m° + 52° = 90°
m° + 52° – 52° = 90° – 52°
m° = 38°
40 + 52 + (38) + n° = 180
130 + n° = 180
130 – 130 + n° = 180 – 130
n° = 50°
d. n° + 62° = 90°
n° + 62° – 62° = 90° – 62°
n° = 28°”
m° + 62° + (28°) + 27° = 180°
m° + 117° = 180
m° + 117° – 117° = 180° – 117°
m° = 63°
Question 2.
Use tools to construct a triangle based on the following given conditions.
a. If possible, use your tools to construct a triangle with angle measurements 20°, 55°, and 105°, and leave evidence of your construction. If it is not possible, explain why.
b. Is it possible to construct two different triangles that have the same angle measurements? If it is, construct examples that demonstrate this condition, and label all angle and length measurements. If it is not possible, explain why.
Answer:
a. Solutions will vary. An example of a correctly constructed triangle is shown here.
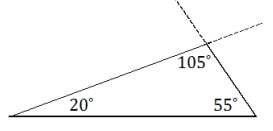
b. Solutions will vary; refer to the rubric.
Question 3.
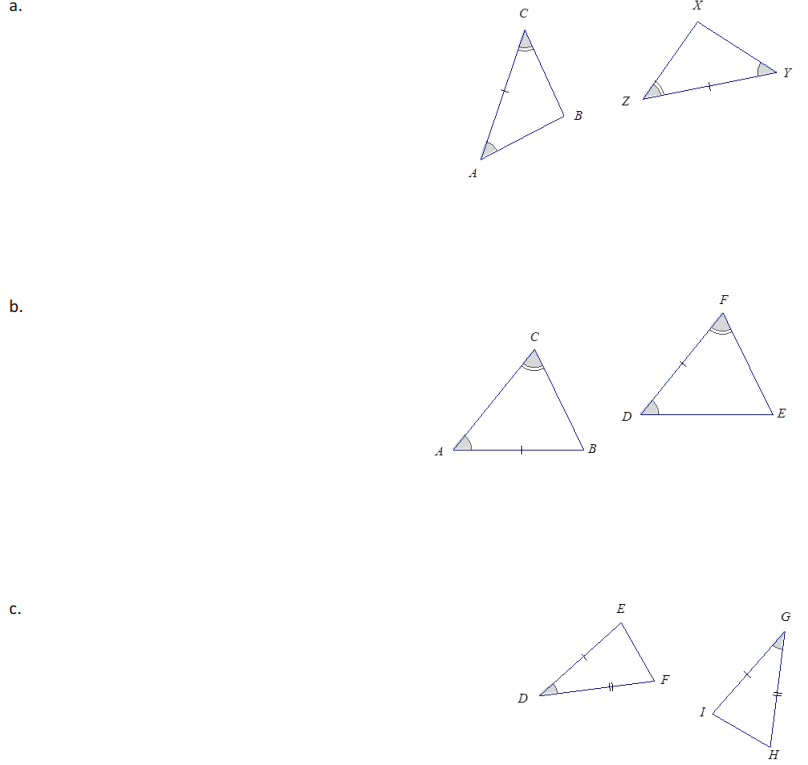
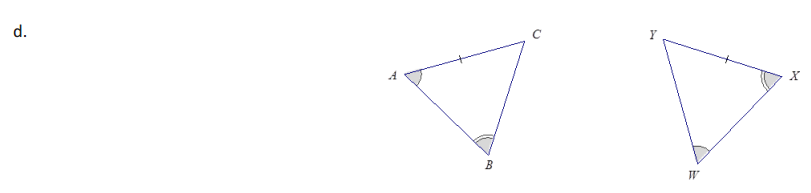
In each of the following problems, two triangles are given. For each: (1) state if there are sufficient or insufficient conditions to show the triangles are identical, and (2) explain your reasoning.
Answer:
a. The triangles are identical by the two angles and included side condition. The marked side is between the given angles.
△ABC ↔ △YXZ
b. There is insufficient evidence to determine that the triangles are identical. In △DEF , the marked side is between the marked angles, but in △ABC , the marked side is not between the marked angles.
c. The triangles are identical by the two sides and included angle condition. △DEF ↔ △GIH
d. The triangles are not identical. In △ABC , the marked side is opposite ∠B . In △WXY , the marked side is opposite ∠W . ∠B and ∠W are not necessarily equal in measure.
Question 4.
Use tools to draw rectangle ABCD with AB = 2 cm and BC = 6 cm. Label all vertices and measurements.
Answer:
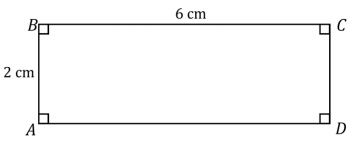
Question 5.
The measures of two complementary angles have a ratio of 3:7. Set up and solve an equation to determine the measurements of the two angles.
Answer:
3x + 7x = 90
10x = 90
(\(\frac{1}{10}\))10x = (\(\frac{1}{10}\))90
x = 9
Measure of Angle 1: 3(9) = 27 . The measure of the first angle is 27° .
Measure of Angle 2: 7(9) = 63 . The measure of the second angle is 63° .
Question 6.
The measure of the supplement of an angle is 12° less than the measure of the angle. Set up and solve an equation to determine the measurements of the angle and its supplement.
Answer:
Let y° be the number of degrees in the angle.
y + (y – 12) = 180
2y – 12 = 180
2y – 12 + 12 = 180 + 12
2y = 192
(\(\frac{1}{2}\))2y = (\(\frac{1}{2}\))192
y = 96
Measure of the angle: 96°
Measure of its supplement: (96)° – 12° = 84°
Question 7.
Three angles are at a point. The ratio of two of the angles is 2:3, and the remaining angle is 32° more than the larger of the first two angles. Set up and solve an equation to determine the measures of all three angles.
Answer:
2x + 3x + (3x + 32) = 360
8x + 32 = 360
8x + 32 – 32 = 360 – 32
8x = 328
(\(\frac{1}{8}\))8x = (\(\frac{1}{8}\))328
x = 41
Measure of Angle 1: 2(41)° = 82°
Measure of Angle 2: 3(41)° = 123°
Measure of Angle 3: 3(41)° + 32° = 155°
Question 8.
Draw a right triangle according to the following conditions, and label the provided information. If it is not possible to draw the triangle according to the conditions, explain why. Include a description of the kind of figure the current measurements allow. Provide a change to the conditions that makes the drawing feasible.
a. Construct a right triangle ABC so that AB = 3 cm, BC = 4 cm, and CA = 5 cm; the measure of angle B is 90°.
b. Construct triangle DEF so that DE = 4 cm, EF = 5 cm, and FD = 11 cm; the measure of angle D is 50°.
Answer:
a.
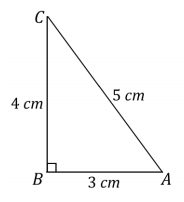
b. It is not possible to draw this triangle because the lengths of the two shorter sides do not sum to be greater than the longest side. In this situation, the total lengths of \(\overline{D E}\) and \(\overline{E F}\) are less than the length of \(\overline{F D}\); there is no way to arrange \(\overline{D E}\) and \(\overline{E F}\) so that they meet. If they do not meet, there is no arrangement of three non-collinear vertices of a triangle; therefore, a triangle cannot be formed. I would change \(\overline{E F}\)to 9 cm instead of 5 cm so that the three sides would form a triangle.