Engage NY Eureka Math 7th Grade Module 6 Lesson 9 Answer Key
Eureka Math Grade 7 Module 6 Lesson 9 Exploratory Challenge Answer Key
Question 1.
A triangle XYZ exists with side lengths of the segments below. Draw △X’Y’Z’ with the same side lengths as △XYZ. Use your compass to determine the sides of △X’Y’Z’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △X’Y’Z’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why. Do the results differ from your predictions?
X ________________ Y
Y _____________________Z
X ___________________________ Z
Answer:
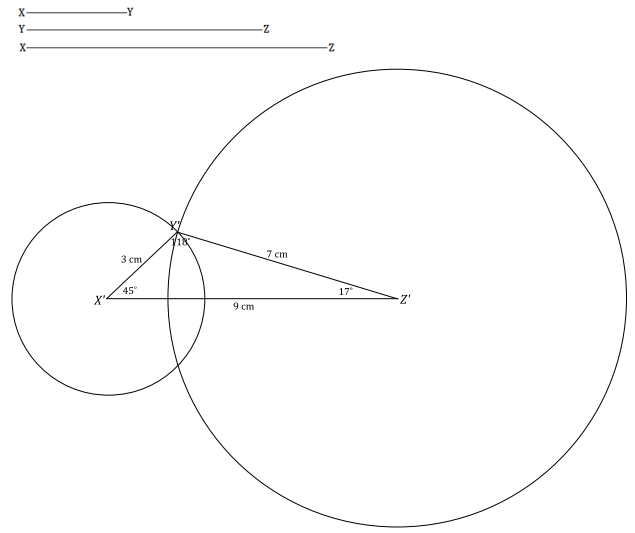
The condition on △X’Y’Z’ is the three side lengths. All of the triangles are identical; the condition determined a unique triangle. After drawing the longest side length, I used the compass to locate the third vertex of the triangle by drawing two circles, one with a radius of the smallest side length and the other with a radius of the medium side length. Each circle was centered at one end of the longest side length. Two possible locations were determined by the intersections of the circles, but both determined the same triangle. One is just a flipped version of the other. The three sides condition determined a unique triangle.
Question 2.
△ABC is located below. Copy the sides of the triangle to create △A’B’C’. Use your compass to determine the sides of △A’B’C’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △A’B’C’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
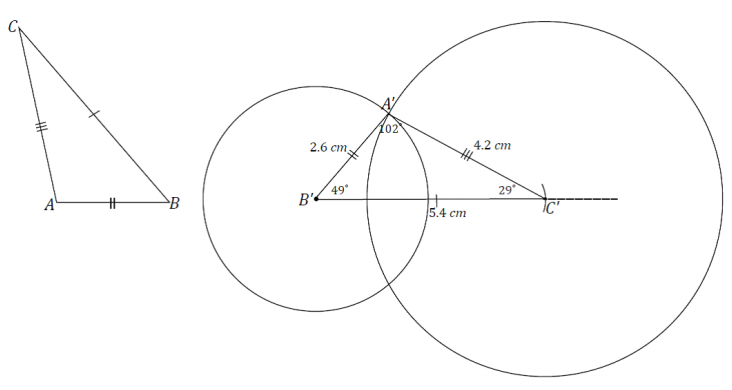
The condition on △A’B’C’ is the three side lengths. All of the triangles are identical; the condition determined a unique triangle. After drawing the longest side length, I used the compass to locate the third vertex of the triangle by drawing two circles, one with a radius of the smallest side length and the other with a radius of the medium side length. Each circle was centered at one end of the longest side length. Two possible locations were determined by the intersections of the circles, but both determined the same triangle. One is just a flipped version of the other. The three sides condition determined a unique triangle.
Question 3.
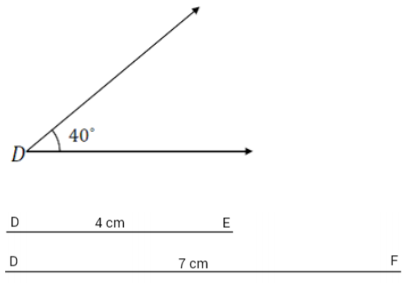
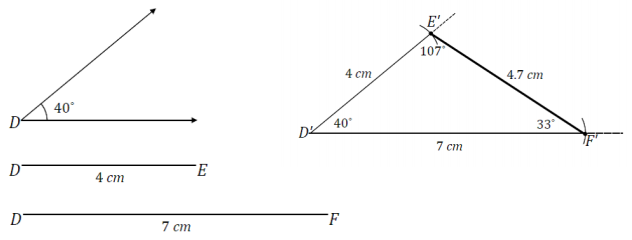
A triangle DEF has an angle of 40° adjacent to side lengths of 4 cm and 7 cm. Construct △D’E’F’ with side lengths
D’ E^’ = 4 cm, D’ F^’ = 7 cm, and included angle ∠D’ = 40°. Use your compass to draw the sides of △D’E’F’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △D’E’F’ drawn? Compare the triangle you drew to two of your peers’ triangles. Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
The condition on △D’E’F’ is two side lengths and the included angle measurement. All of the triangles are identical; the condition determined a unique triangle. Once the 40° angle is drawn and the 4 cm and 7 cm side lengths are marked off on the rays of the angle, there is only one place the third side of the triangle can be. Therefore, all triangles drawn under this condition will be identical. Switching the 4 cm and 7 cm sides also gives a triangle satisfying the conditions, but it is just a flipped version of the other.
Question 4.
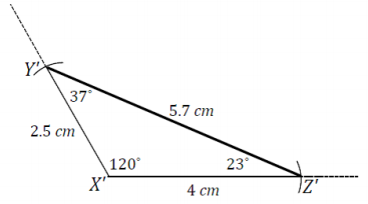
△XYZ has side lengths XY = 2.5 cm, XZ = 4 cm, and ∠X = 120°. Draw △X’Y’Z’ under the same conditions. Use your compass and protractor to draw the sides of △X’Y’Z’. Use your ruler to measure side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is △X’Y’Z’ drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
The condition on △X’Y’Z’ is two side lengths and the included angle measurement. The triangle is identical to other triangles drawn under this condition; the conditions produced a unique triangle. Once the 120° angle is drawn and the 2.5 cm and 7 cm side lengths are marked off on the rays of the angle, there is only one place the third side of the triangle can be. Therefore, all triangles drawn under these conditions will be identical. Switching the 2.5 cm and 7 cm sides also gives a triangle satisfying the conditions, but it is just a flipped version of the other.
Eureka Math Grade 7 Module 6 Lesson 9 Problem Set Answer Key
Question 1.
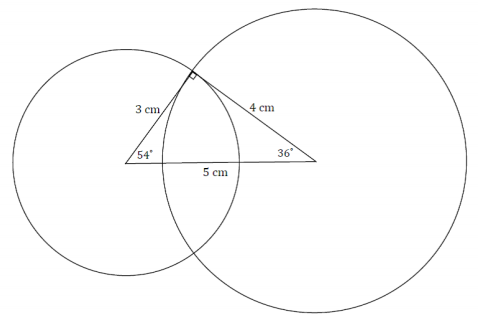
A triangle with side lengths 3 cm, 4 cm, and 5 cm exists. Use your compass and ruler to draw a triangle with the same side lengths. Leave all construction marks as evidence of your work, and label all side and angle measurements.
Under what condition is the triangle drawn? Compare the triangle you drew to two of your peers’ triangles. Are the triangles identical? Did the condition determine a unique triangle? Use your construction to explain why.
Answer:
The triangles are identical; the three sides condition determined a unique triangle. After drawing the longest side length, I used the compass to locate the third vertex of the triangle by drawing two circles, one with a radius of the smallest side length and the other with a radius of the medium side length. Each circle was centered at one end of the longest side length. Two possible locations were determined by the intersections of the circles, but both determined the same triangle; one is just a flipped version of the other. The three sides condition determined a unique triangle.
Question 2.
Draw triangles under the conditions described below.
a. A triangle has side lengths 5 cm and 6 cm. Draw two nonidentical triangles that satisfy these conditions. Explain why your triangles are not identical.
b. A triangle has a side length of 7 cm opposite a 45° angle. Draw two nonidentical triangles that satisfy these conditions. Explain why your triangles are not identical.
Answer:
a. Solutions will vary; check to see that the conditions are satisfied in each triangle. The triangles cannot be identical because there is no correspondence that will match equal corresponding sides and equal angles between the triangles.
b. Solutions will vary; check to see that the conditions are satisfied in each triangle. The triangles cannot be identical because there is no correspondence that will match equal corresponding sides and equal angles between the triangles.
Question 3.
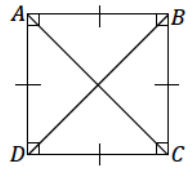
Diagonal \(\overline{B D}\) is drawn in square ABCD. Describe what condition(s) can be used to justify that △ABD is identical to △CBD. What can you say about the measures of ∠ABD and ∠CBD? Support your answers with a diagram and explanation of the correspondence(s) that exists.
Answer:
Two possible conditions can be used to justify that △ABD is identical to △CBD:
△ABD is identical to △CBD by the two sides and included angle condition. Since all four sides of a square are equal in length, AB = CB and AD = CD.
All four angles in a square are right angles; therefore, they are equal in measurement: ∠A = ∠C. The two sides and included angle condition is satisfied by the same measurements in both triangles. Since the two sides and included angle condition determine a unique triangle, △ABD must be identical to △CBD. The correspondence △ABD ↔ △CBD matches corresponding equal sides and corresponding angles. It matches ∠ABD with ∠CBD, so the two angles have equal measure and angle sum of 90°; therefore, each angle measures 45°.
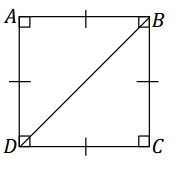
△ABD is identical to △CBD by the three sides condition. Again, all four sides of the square are equal in length; therefore, AB = CB, and AD = CD. \(\overline{B D}\) is a side to both △ABD and △CBD, and BD = BD. The three sides condition is satisfied by the same measurements in both triangles. Since the three sides condition determines a unique triangle, △ABD must be identical to △CBD. The correspondence △ABD ↔ △CBD matches equal corresponding sides and equal corresponding angles. It matches ∠ABD with ∠CBD, so the two angles have equal measure and angle sum of 90°; therefore, each angle measures 45°.
Question 4.
Diagonals \(\overline{B D}\) and \(\overline{A C}\) are drawn in square ABCD. Show that △ABC is identical to △BAD, and then use this information to show that the diagonals are equal in length.
Answer:
Use the two sides and included angle condition to show △ABC is identical to
△BAD; then, use the correspondence △ABC ↔ △BAD to conclude AC = BD.
△ABC is identical to △BAD by the two sides and included angle condition. Since \(\overline{A B}\) and \(\overline{B A}\) determine the same line segment, AB = BA. Since all four sides of a square are equal in length, then BC=AD. All four angles in a square are right angles and are equal in measurement; therefore, ∠B = ∠A. The two sides and included angle condition is satisfied by the same measurements in both triangles. Since the two sides and included angle condition determines a unique triangle, △ABC must be identical to △BAD. The correspondence
△ABC ↔ △BAD matches corresponding equal sides and corresponding equal angles. It matches the diagonals \(\overline{A C}\) and \(\overline{B D}\). Therefore, AC=BD.
Question 5.
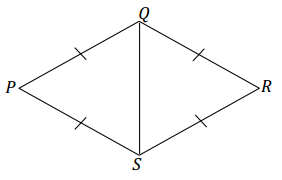
Diagonal \(\overline{Q S}\) is drawn in rhombus PQRS. Describe the condition(s) that can be used to justify that △PQS is identical to △RQS. Can you conclude that the measures of ∠PQS and ∠RQS are the same? Support your answer with a diagram and explanation of the correspondence(s) that exists.
Answer:
△PQS is identical to △RQS by the three sides condition. All four sides of a rhombus are equal in length; therefore, PQ = RQ and PS = RS. \(\overline{Q S}\) is a side to both △PQS and △RQS, and QS = QS. The three sides condition is satisfied by the same measurements in both triangles. Since the three sides condition determines a unique triangle, △PQS must be identical to
△RQS. The correspondence △PQS ↔ △RQS matches equal corresponding sides and equal corresponding angles. The correspondence matches ∠PQS and ∠RQS; therefore, they must have the same measure.
Question 6.
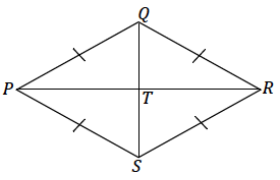
Diagonals \(\overline{Q S}\) and \(\overline{P R}\) are drawn in rhombus PQRS and meet at point T. Describe the condition(s) that can be used to justify that △PQT is identical to △RQT. Can you conclude that the line segments PR and QS are perpendicular to each other? Support your answers with a diagram and explanation of the correspondence(s) that exists.
Answer:
△PQT is identical to △RQT by the two sides and included angle condition. All four sides of a rhombus are equal in length; therefore, PQ = RQ. \(\overline{Q T}\) is a side to both △PQT and △RQT, and QT = QT. Since T lies on segment QS, then ∠PQT = ∠PQS and ∠RQT = ∠RQS. By Problem 5, ∠PQT=∠RQT, and the two sides and included angle condition is satisfied by the same measurements in both triangles. Since the two sides and included angle condition determines a unique triangle, then △PQT must be identical to △RQT. The correspondence △PQT↔△RQT matches equal corresponding sides and equal corresponding angles. The correspondence matches ∠PTQ and ∠RTQ; therefore, they must have the same measure. The angle sum of ∠PTQ and ∠RTQ is 180°; therefore, each angle is 90°, and the diagonals are perpendicular
to each other.
Eureka Math Grade 7 Module 6 Lesson 9 Exit Ticket Answer Key
Question 1.
Choose either the three sides condition or the two sides and included angle condition, and explain why the condition determines a unique triangle.
In drawing a triangle with three provided side lengths, there is only one way to draw the triangle. After drawing one length, use the other two lengths to draw circles with the lengths as the respective radii of each circle, centered at either end of the segment drawn first. Regardless of which order of segments is used, there is only one unique triangle that can be drawn.
Answer:
In drawing a triangle with two side lengths and included angle provided, there is only one way to draw the triangle. After drawing the angle and marking off the two side lengths on the rays of the angle, there is only one possible place to position the third side of the triangle, which also determines the two remaining angle measures of the triangle. Therefore, the two sides and included angle condition determines a unique triangle.