Eureka Math Grade 7 Module 6 Lesson 6 Answer Key

Engage NY Eureka Math 7th Grade Module 6 Lesson 6 Answer Key

Eureka Math Grade 7 Module 6 Lesson 6 Exploratory Challenge Answer Key

Use a ruler, protractor, and compass to complete the following problems.
Question 1.
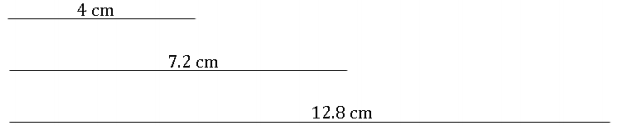
Use your ruler to draw three segments of the following lengths: 4 cm, 7.2 cm, and 12.8 cm. Label each segment with its measurement.
Answer:

Question 2.
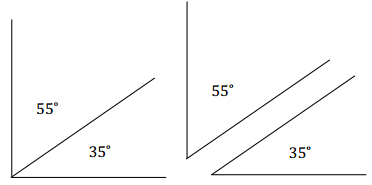
Draw complementary angles so that one angle is 35°. Label each angle with its measurement. Are the angles required to be adjacent?
Answer:
The complementary angles do not need to be adjacent; the sum of the measurements of the angles needs to be 90°.

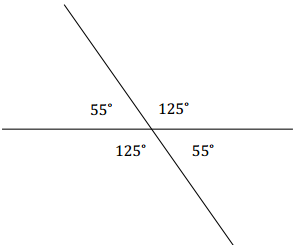
Question 3.
Draw vertical angles so that one angle is 125°. Label each angle formed with its measurement.
Answer:

Question 4.
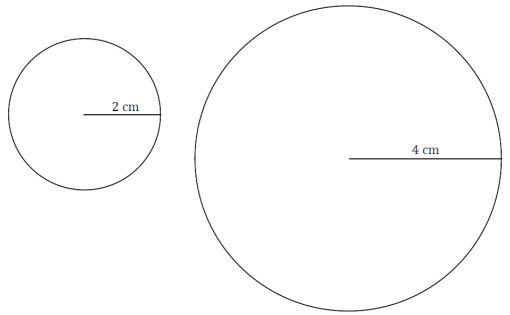
Draw three distinct segments of lengths 2 cm, 4 cm, and 6 cm. Use your compass to draw three circles, each with a radius of one of the drawn segments. Label each radius with its measurement.
Answer:
Due to space restrictions, only the two smaller circles are shown here:

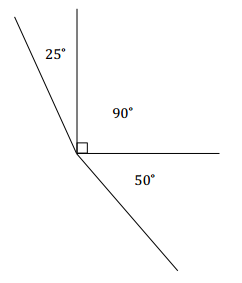
Question 5.
Draw three adjacent angles a, b, and c so that a = 25°, b = 90°, and c = 50°. Label each angle with its measurement.
Answer:

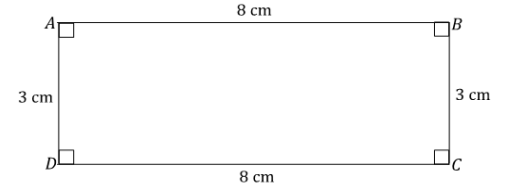
Question 6.
Draw a rectangle ABCD so that AB = CD = 8 cm and BC = AD = 3 cm.
Answer:

Question 7.
Draw a segment AB that is 5 cm in length. Draw a second segment that is longer than \(\overline{A B}\), and label one endpoint C. Use your compass to find a point on your second segment, which will be labeled D, so that CD = AB.
Answer:

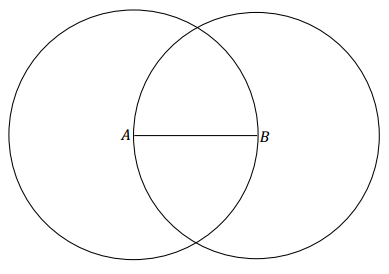
Question 8.
Draw a segment AB with a length of your choice. Use your compass to construct two circles:
i) A circle with center A and radius AB.
ii) A circle with center B and radius BA.
Describe the construction in a sentence.
Answer:
Two circles with radius AB are drawn; one has its center at A, and the other has its center at B.

Question 9.
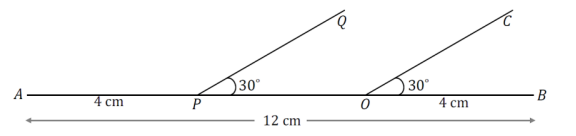
Draw a horizontal segment AB, 12 cm in length.
a. Label a point O on \(\overline{A B}\) that is 4 cm from B.
b. Point O will be the vertex of an angle COB.
c. Draw ray OC so that the ray is above \(\overline{A B}\) and ∠COB = 30°.
d. Draw a point P on \(\overline{A B}\)̅ that is 4 cm from A.
e. Point P will be the vertex of an angle QPO.
f. Draw ray PQ so that the ray is above \(\overline{A B}\) and ∠QPO = 30°.
Answer:

Question 10.
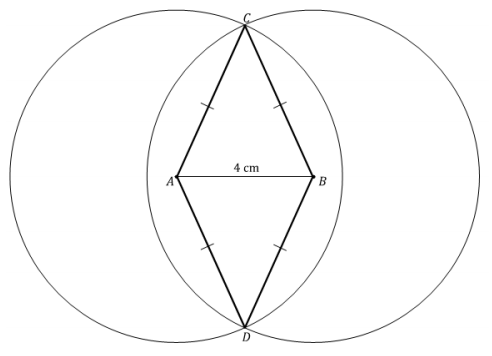
Draw segment AB of length 4 cm. Draw two circles that are the same size, one with center A and one with center B (i.e., do not adjust your compass in between) with a radius of a length that allows the two circles to intersect in two distinct locations. Label the points where the two circles intersect C and D. Join A and C with a segment; join B and C with a segment. Join A and D with a segment; join B and D with a segment.
What kind of triangles are △ABC and △ABD? Justify your response.
Answer:
△ABC and △ABD are identical isosceles triangles. Both circles are the same size (i.e., have the same radius). Furthermore, the point along each circle is the same distance away from the center no matter where you are on the circle; this means the distance from A to C is the same as the distance from B to C (the same follows for D).
A triangle with at least two sides of equal length is an isosceles triangle.
Possible solution:

Question 11.
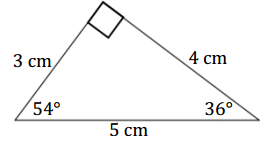
Determine all possible measurements in the following triangle, and use your tools to create a copy of it.

Answer:

Eureka Math Grade 7 Module 6 Lesson 6 Problem Set Answer Key

Use a ruler, protractor, and compass to complete the following problems.
Question 1.
Draw a segment AB that is 5 cm in length and perpendicular to segment CD, which is 2 cm in length.
Answer:
One possible solution:

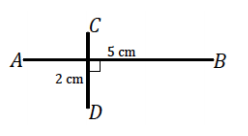
Question 2.
Draw supplementary angles so that one angle is 26°. Label each angle with its measurement.
Answer:
Possible solutions:

Question 3.
Draw △ABC so that ∠B has a measurement of 100°.
Answer:
One possible solution:

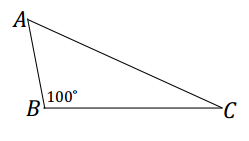
Question 4.
Draw a segment AB that is 3 cm in length. Draw a circle with center A and radius AB. Draw a second circle with diameter AB.
Answer:
One possible solution:

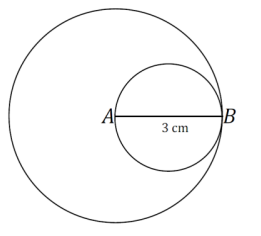
Question 5.
Draw an isosceles △ABC. Begin by drawing ∠A with a measurement of 80°. Use the rays of ∠A as the equal legs of the triangle. Choose a length of your choice for the legs, and use your compass to mark off each leg. Label each marked point with B and C. Label all angle measurements.
Answer:
One possible solution:

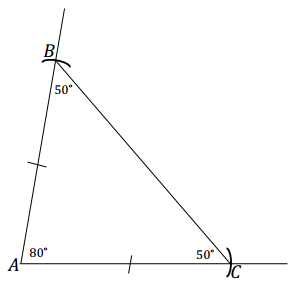
Question 6.
Draw an isosceles △DEF. Begin by drawing a horizontal segment DE that is 6 cm in length. Use your protractor to draw ∠D and ∠E so that the measurements of both angles are 30°. If the non-horizontal rays of ∠D and ∠E do not already cross, extend each ray until the two rays intersect. Label the point of intersection F. Label all side and angle measurements.
Answer:
One possible solution:

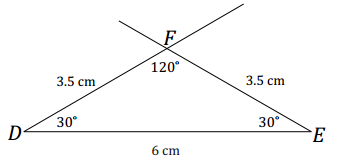
Question 7.
Draw a segment AB that is 7 cm in length. Draw a circle with center A and a circle with center B so that the circles are not the same size, but do intersect in two distinct locations. Label one of these intersections C. Join A to C and B to C to form △ABC.
Answer:
One possible solution:

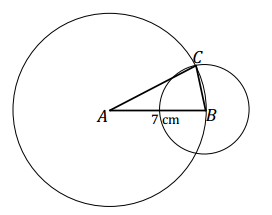
Question 8.
Draw an isosceles trapezoid WXYZ with two equal base angles, ∠W and ∠X, that each measures 110°. Use your compass to create the two equal sides of the trapezoid. Leave arc marks as evidence of the use of your compass. Label all angle measurements. Explain how you constructed the trapezoid.
Answer:

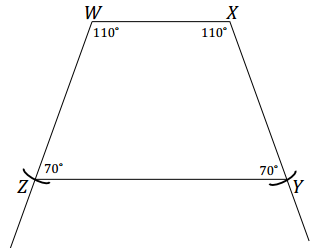
Draw segment WX. Use a protractor and segment WX to draw ∠XWZ at a measurement of 110°; do the same to draw ∠WXY. (Note: When drawing \(\overrightarrow{W Z}\) and \(\overrightarrow{X Y}\), length is not specified, so students should have rays long enough so that they can use a compass to mark off lengths that are the same along each ray in the next step.) Place the point of the compass at W, adjust the compass to a desired width, and mark an arc so that it crosses \(\overrightarrow{W Z}\). Label the intersection as Z. Do the same from X along \(\overrightarrow{X Y}\), and mark the intersection as Y. Finally, join Z and Y to form isosceles trapezoid WXYZ.

Eureka Math Grade 7 Module 6 Lesson 6 Exit Ticket Answer Key

Question 1.
Draw a square PQRS with side length equal to 5 cm. Label the side and angle measurements.
Answer:

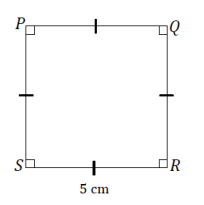
Question 2.
Draw a segment AB, 6 cm in length. Draw a circle whose diameter is segment AB.
Answer: