Engage NY Eureka Math 7th Grade Module 4 Lesson 4 Answer Key
Eureka Math Grade 7 Module 4 Lesson 4 Example Answer Key
Example 1: Finding a Percent Increase
Cassandra’s aunt said she will buy Cassandra another ring for her birthday. If Cassandra gets the ring for her birthday, what will be the percent increase in her ring collection?

Answer:
→ Looking back at our answers to the Opening Exercise, what percent is represented by 1 ring? If Cassandra gets the ring for her birthday, by what percent did her ring collection increase?
20% represents 1 ring, so her ring collection would increase by 20%.
→ Compare the number of new rings to the original total:
\(\frac{1}{5}\) = \(\frac{20}{100}\) = 0.20 = 20%
→ Use an algebraic equation to model this situation. The quantity is represented by the number of new rings.
Quantity = Percent × Whole. Let p represent the unknown percent.
1 = p∙5
\(\frac{1}{5}\) = p
\(\frac{1}{5}\) = \(\frac{20}{100}\) = 0.2 = 20%
Example 2: Percent Decrease
Ken said that he is going to reduce the number of calories that he eats during the day. Ken’s trainer asked him to start off small and reduce the number of calories by no more than 7%.
Ken estimated and consumed 2,200 calories per day instead of his normal 2,500 calories per day until his next visit with the trainer. Did Ken reduce his calorie intake by no more than 7%? Justify your answer.
Answer:
a. Ken reduced his daily calorie intake by 300 calories. Does 7% of 2,500 calories equal 300 calories?
Quantity = Percent × Whole
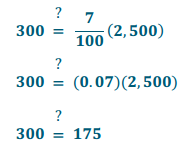
False, because 300≠175.
b. A 7% decrease means Ken would get 93% of his normal daily calorie intake since 100% – 7% = 93%. Ken consumed 2,200 calories, so does 93% of 2,500 equal 2,200?
Quantity = Percent × Whole
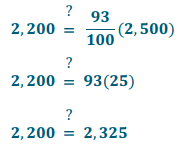
False. Because 2,200 ≠ 2,325, Ken’s estimation was wrong.
Example 3: Finding a Percent Increase or Decrease
Justin earned 8 badges in Scouts as of the Scout Master’s last report. Justin wants to complete 2 more badges so that he will have a total of 10 badges earned before the Scout Master’s next report.
a. If Justin completes the additional 2 badges, what will be the percent increase in badges?
Answer:
Quantity = Percent × Whole. Let p represent the unknown percent.
2 = p∙8
2(\(\frac{1}{8}\)) = p(\(\frac{1}{8}\))(8)
\(\frac{2}{8}\) = p
\(\frac{1}{4}\) = p
\(\frac{1}{4}\) = \(\frac{25}{100}\) = 25%
There would be a 25% increase in the number of badges.
b. Express the 10 badges as a percent of the 8 badges.
Answer:
8 badges is the whole, or 100%, and 2 badges represent 25% of the badges, so 10 badges represent
100% + 25% = 125% of the 8 badges.
Check:
10 = p∙8
10(\(\frac{1}{8}\)) = p(\(\frac{1}{8}\))(8)
\(\frac{10}{8}\) = p
\(\frac{5}{4}\) = p
\(\frac{5}{4}\) = \(\frac{125}{100}\) = 125%
c. Does 100% plus your answer in part (a) equal your answer in part (b)? Why or why not?
Answer:
Yes. My answer makes sense because 8 badges are the whole or 100%, and 2 badges represent 25% of the badges, so 10 badges represent 100% + 25%, or 125% of the 8 badges.
Example 4: Finding the Original Amount Given a Percent Increase or Decrease
The population of cats in a rural neighborhood has declined in the past year by roughly 30%. Residents hypothesize that this is due to wild coyotes preying on the cats. The current cat population in the neighborhood is estimated to be 12. Approximately how many cats were there originally?
Answer:
→ Do we know the part or the whole?
We know the part (how many cats are left), but we do not know the original whole.
→ Is this a percent increase or decrease problem? How do you know?
Percent decrease because the word declined means decreased.
→ If there was about a 30% decline in the cat population, then what percent of cats remain?
100% – 30% = 70%, so about 70% of the cats remain.
→ How do we write an equation to model this situation?
12 cats represent the quantity that is about 70% of the original number of cats. We are trying to find the whole, which equals the original number of cats. So, using Quantity = Percent × Whole and substituting the known values into the equation, we have 12 = 70%∙W, where W represents the original number of cats.
Quantity = Percent × Whole
12 = (\(\frac{7}{10}\))∙W
(12)(\(\frac{10}{7}\)) = (\(\frac{7}{10}\))(\(\frac{10}{7}\))∙W
\(\frac{120}{7}\) = W
W≈17.1≈17
There must have been 17 cats originally.

To find the original number of cats or the whole (100% of the cats), we need to add three more twelve sevenths to 12.
12 + 3(\(\frac{12}{7}\)) = \(\frac{84}{7}\) + \(\frac{36}{7}\) = \(\frac{120}{7}\)≈17
The decrease was given as approximately 30%, so there must have been 17 cats originally.
Example 5.
Lu’s math score on her achievement test in seventh grade was a 650. Her math teacher told her that her test level went up by 25% from her sixth grade test score level. What was Lu’s test score level in sixth grade?
Answer:
→ Does this represent a percent increase or decrease? How do you know?
Percent increase because the word up means increase.
→ Using the equation Quantity = Percent × Whole, what information do we know?
We know Lu’s test score level in seventh grade after the change, which is the quantity, and we know the percent. But we do not know the whole (her test score level from sixth grade).
→ If Lu’s sixth grade test score level represents the whole, then what percent represents the seventh grade level?
100% + 25% = 125%
→ How do we write an equation to model this situation? Let W represent Lu’s test score in sixth grade.
Quantity = Percent × Whole
650 = 125% × W
650 = 1.25W
650(\(\frac{1}{1.25}\)) = 1.25(\(\frac{1}{1.25}\))W
\(\frac{650}{1.25}\) = W
\(\frac{65,000}{125}\) = W
520 = W
Lu’s sixth grade test score level was 520.
Eureka Math Grade 7 Module 4 Lesson 4 Exercise Answer Key
Opening Exercise
Cassandra likes jewelry. She has 5 rings in her jewelry box.
a. In the box below, sketch Cassandra’s 5 rings.
Answer:
b. Draw a double number line diagram relating the number of rings as a percent of the whole set of rings.
Answer:
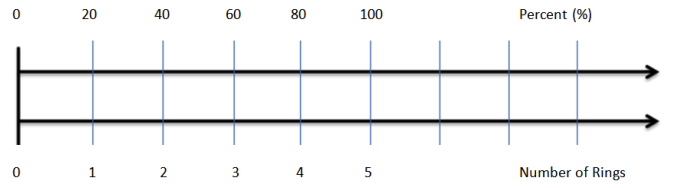
c. What percent is represented by the whole collection of rings? What percent of the collection does each ring represent?
Answer:
100%, 20%
Exercise 1.
a. Jon increased his trading card collection by 5 cards. He originally had 15 cards. What is the percent increase? Use the equation Quantity = Percent × Whole to arrive at your answer, and then justify your answer using a numeric or visual model.
Answer:
Quantity = Percent × Whole. Let p represent the unknown percent.
5 = p(15)
5(\(\frac{1}{15}\)) = p(15)(\(\frac{1}{15}\))
\(\frac{5}{15}\) = p
p = \(\frac{1}{3}\) = 0.3333…
0.3333 … = \(\frac{33}{100}\) + \(\frac{0.3333 \ldots}{100}\) = 33% + \(\frac{1}{3}\)% = 33\(\frac{1}{3}\)%
b. Suppose instead of increasing the collection by 5 cards, Jon increased his 15 – card collection by just 1 card. Will the percent increase be the same as when Cassandra’s ring collection increased by 1 ring (in Example 1)? Why or why not? Explain.
Answer:
No, it would not be the same because the part – to – whole relationship is different. Cassandra’s additional ring compared to the original whole collection was 1 to 5, which is equivalent to 20 to 100, which is 20%. Jon’s additional trading card compared to his original card collection is 1 to 15, which is less than 10%, since
\(\frac{1}{15}\)<\(\frac{1}{10}\), and \(\frac{1}{10}\) = 10%.
c. Based on your answer to part (b), how is displaying change as a percent useful?
Answer:
Representing change as a percent helps us to understand how large the change is compared to the whole.
Discussion
A sales representative is taking 10% off of your bill as an apology for any inconveniences.

Answer:

Exercise 2.
Skylar is answering the following math problem:
The value of an investment decreased by 10%. The original amount of the investment was $75.00. What is the current value of the investment?
a. Skylar said 10% of $75.00 is $7.50, and since the investment decreased by that amount, you have to subtract $7.50 from $75.00 to arrive at the final answer of $67.50. Create one algebraic equation that can be used to arrive at the final answer of $67.50. Solve the equation to prove it results in an answer of $67.50. Be prepared to explain your thought process to the class.
Answer:
Let F represent the final value of the investment.
The final value is 90% of the original investment, since 100% – 10% = 90%.
F = Percent × Whole
F = (0.90)(75)
F = 67.5
The final value of the investment is $67.50.
b. Skylar wanted to show the proportional relationship between the dollar value of the original investment, x, and its value after a 10% decrease, y. He creates the table of values shown below. Does it model the relationship? Explain. Then, provide a correct equation for the relationship Skylar wants to model.
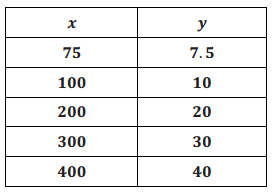
Answer:
No. The table only shows the proportional relationship between the amount of the investment and the amount of the decrease, which is 10% of the amount of the investment. To show the relationship between the value of the investment before and after the 10% decrease, he needs to subtract each value currently in the y – column from each value in the x – column so that the y – column shows the following values: 67.5, 90, 180, 270, and 360. The correct equation is y = x – 0.10x, or y = 0.90x.
Eureka Math Grade 7 Module 4 Lesson 4 Problem Set Answer Key
Question 1.
A store advertises 15% off an item that regularly sells for $300.
a. What is the sale price of the item?
Answer:
(0.85)300 = 255; the sale price is $255.
b. How is a 15% discount similar to a 15% decrease? Explain.
Answer:
In both cases, you are subtracting 15% of the whole from the whole, or finding 85% of the whole.
c. If 8% sales tax is charged on the sale price, what is the total with tax?
Answer:
(1.08)(255) = 275.40; the total with tax is $275.40.
d. How is 8% sales tax like an 8% increase? Explain.
Answer:
In both cases, you are adding 8% of the whole to the whole, or finding 108% of the whole.
Question 2.
An item that was selling for $72.00 is reduced to $60.00. Find the percent decrease in price. Round your answer to the nearest tenth.
Answer:
The whole is 72. 72 – 60 = 12. 12 is the part. Using Quantity = Percent × Whole, I get 12 = p × 72, where p represents the unknown percent, and working backward, I arrive at \(\frac{12}{72}\) = \(\frac{1}{6}\) = \(0.1 \overline{6}\) = p.
So, it is about a 16.7% decrease.
Question 3.
A baseball team had 80 players show up for tryouts last year and this year had 96 players show up for tryouts. Find the percent increase in players from last year to this year.
Answer:
The number of players that showed up last year is the whole; 16 players are the quantity of change since
96 – 80 = 16.
Quantity = Percent × Whole. Let p represent the unknown percent.
16 = p(80)
p = 0.2
0.2 = \(\frac{20}{100}\) = 20%
The number of players this year was a 20% increase from last year.
Question 4.
At a student council meeting, there was a total of 60 students present. Of those students, 35 were female.
a. By what percent is the number of females greater than the number of males?
Answer:
The number of males (60 – 35 = 25) at the meeting is the whole. The part (quantity) can be represented by the number of females (35) or how many more females there are than the number of males.
Quantity = Percent × Whole
35 = p(25)
p = 1.4
1.4 = 140%, which is 40% more than 100%. Therefore, there were 40% more females than males at the student council meeting.
b. By what percent is the number of males less than the number of females?
Answer:
The number of females (35) at the meeting is the whole. The part (quantity) can be represented by the number of males, or the number less of males than females (10).
Quantity = Percent × Whole
10 = p(35)
p≈0.29
0.29 = 29%
The number of males at the meeting is approximately 29% less than the number of females.
c. Why is the percent increase and percent decrease in parts (a) and (b) different?
Answer:
The difference in the number of males and females is the same in each case, but the whole quantities in parts (a) and (b) are different.
Question 5.
Once each day, Darlene writes in her personal diary and records whether the sun is shining or not. When she looked back though her diary, she found that over a period of 600 days, the sun was shining 60% of the time. She kept recording for another 200 days and then found that the total number of sunny days dropped to 50%. How many of the final 200 days were sunny days?
Answer:
To find the number of sunny days in the first 600 days, the total number of days is the whole.
Quantity = Percent × Whole. Let s represent the number of sunny days.
s = 0.6(600)
s = 360
There were 360 sunny days in the first 600 days.
The total number of days that Darlene observed was 800 days because 600 + 200 = 800.
d = 0.5(800)
d = 400
There was a total of 400 sunny days out of the 800 days.
The number of sunny days in the final 200 days is the difference of 400 days and 360 days.
400 – 360 = 40, so there were 40 sunny days of the last 200 days.
Question 6.
Henry is considering purchasing a mountain bike. He likes two bikes: One costs $500, and the other costs $600. He tells his dad that the bike that is more expensive is 20% more than the cost of the other bike. Is he correct? Justify your answer.
Answer:
Yes. Quantity = Percent × Whole. After substituting in the values of the bikes and percent, I arrive at the following equation: 600 = 1.2(500), which is a true equation.
Question 7.
State two numbers such that the lesser number is 25% less than the greater number.
Answer:
Answers will vary. One solution is as follows: Greater number is 100; lesser number is 75.
Question 8.
State two numbers such that the greater number is 75% more than the lesser number.
Answer:
Answers will vary. One solution is as follows: Greater number is 175; lesser number is 100.
Question 9.
Explain the difference in your thought process for Problems 7 and 8. Can you use the same numbers for each problem? Why or why not?
Answer:
No. The whole is different in each problem. In Problem 7, the greater number is the whole. In Problem 8, the lesser number is the whole.
Question 10.
In each of the following expressions, c represents the original cost of an item.

a. Circle the expression(s) that represents 10% of the original cost. If more than one answer is correct, explain why the expressions you chose are equivalent.
b. Put a box around the expression(s) that represents the final cost of the item after a 10% decrease. If more than one is correct, explain why the expressions you chose are equivalent.
Answer:
c – 0.10c
1c – 0.10c Multiplicative identity property of 1
(1 – 0.10)c Distributive property (writing a sum or difference as a product)
0.90c
Therefore, c – 0.10c = 0.90c.
c. Create a word problem involving a percent decrease so that the answer can be represented by expression (ii).
Answer:
Answers will vary. The store’s cashier told me I would get a 10% discount on my purchase. How can I find the amount of the 10% discount?
d. Create a word problem involving a percent decrease so that the answer can be represented by expression (i).
Answer:
Answers will vary. An item is on sale for 10% off. If the original price of the item is c, what is the final price after the 10% discount?
e. Tyler wants to know if it matters if he represents a situation involving a 25% decrease as 0.25x or (1 – 0.25)x. In the space below, write an explanation that would help Tyler understand how the context of a word problem often determines how to represent the situation.
Answer:
If the word problem asks you to find the amount of the 25% decrease, then 0.25x would represent it. If the problem asks you to find the value after a 25% decrease, then (1 – 0.25)x would be a correct representation.
Eureka Math Grade 7 Module 4 Lesson 4 Exit Ticket Answer Key
Question 1.
Erin wants to raise her math grade to a 95 to improve her chances of winning a math scholarship. Her math average for the last marking period was an 81. Erin decides she must raise her math average by 15% to meet her goal. Do you agree? Why or why not? Support your written answer by showing your math work.
Answer:
No, I do not agree. 15% of 81 is 12.15. 81 + 12.15 = 93.15, which is less than 95. I arrived at my answer using the equation below to find 15% of 81.
Quantity = Percent × Whole
Let G stand for the number of points Erin’s grade will increase by after a 15% increase from 81. The whole is 81, and the percent is 15%. First, I need to find 15% of 81 to arrive at the number of points represented by a 15% increase. Then, I will add that to 81 to see if it equals 95, which is Erin’s goal.
G = 0.15 × 81
G = 12.15
Adding the points onto her average: 81.00 + 12.15 = 93.15
Comparing it to her goal: 93.15 < 95