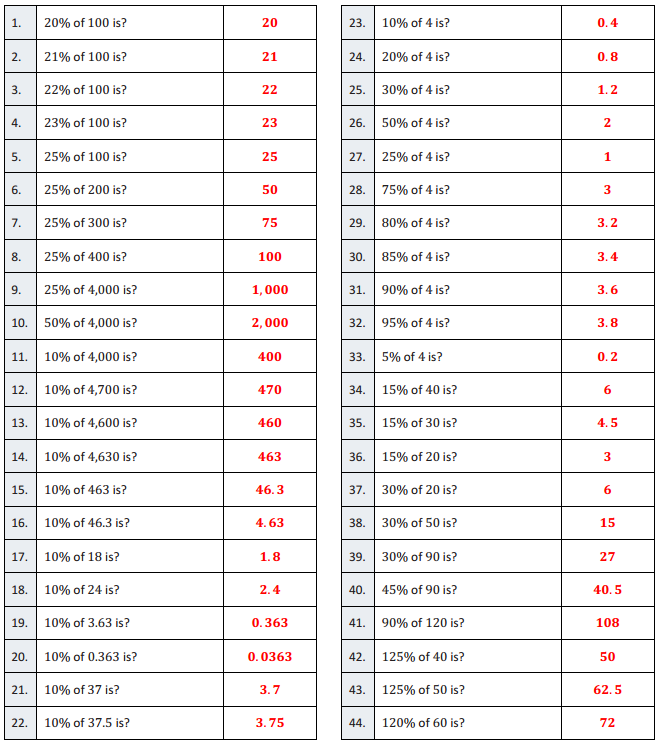
Engage NY Eureka Math 7th Grade Module 4 Lesson 3 Answer Key
Eureka Math Grade 7 Module 4 Lesson 3 Example Answer Key
Example
a. The members of a club are making friendship bracelets to sell to raise money. Anna and Emily made 54 bracelets over the weekend. They need to produce 300 bracelets by the end of the week. What percent of the bracelets were they able to produce over the weekend?
Answer:
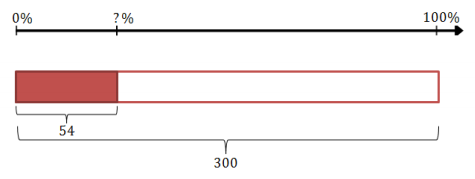
300 → 100%
1 → \(\frac{100}{300}\)%
54 → 54 ∙ \(\frac{100}{300}\)%
54 → 54 ∙ \(\frac{1}{3}\)%
54 → 18%
Anna and Emily were able to produce 18% of the total number of bracelets over the weekend
Quantity = Percent × Whole
Let p represent the unknown percent.
54 = p(300)
\(\frac{1}{300}\) (54) = \(\frac{1}{300}\) (300)p
\(\frac{54}{300}\) = 1p
\(\frac{18}{100}\) = p
\(\frac{18}{100}\) = 0.18 = 18%
Anna and Emily were able to produce 18% of the total bracelets over the weekend.
b. Anna produced 32 of the 54 bracelets produced by Emily and Anna over the weekend. Write the number of bracelets that Emily produced as a percent of those that Anna produced.
Answer:
Arithmetic Method:
32 → 100%
1 → \(\frac{100}{32}\)%
22 → 22 ∙ \(\frac{100}{32}\)%
22 → 100 ∙ \(\frac{22}{32}\)%
22 → 100 ∙ 0.6875%
22 → 68.75%
Algebraic Method:
Quantity = Percent × Whole
Let p represent the unknown percent.
22 = p(32)
\(\frac{1}{32}\) (22) = \(\frac{1}{32}\) (32)p
\(\frac{22}{32}\) = 1p
0.6875 = p
0.6875 = 68.75%
22 bracelets are 68.75% of the number of bracelets that Anna produced. Emily produced 22 bracelets; therefore, she produced 68.75% of the number of bracelets that Anna produced.
c. Write the number of bracelets that Anna produced as a percent of those that Emily produced.
Answer:
Arithmetic Method:
22 → 100%
1 → \(\frac{100}{22}\)%
32 → 32 ∙ \(\frac{100}{22}\)%
32 → 100 ∙ \(\frac{32}{22}\)%
32 → 100 ∙ \(\frac{16}{11}\)%
32 → \(\frac{1600}{11}\)%
32 → 145 \(\frac{5}{11}\)%
Algebraic Method:
Quantity = Percent × Whole
Let p represent the unknown percent.
32 = p(22)
\(\frac{1}{22}\) (32) = \(\frac{1}{22}\) (22)p
\(\frac{32}{22}\) = 1p
\(\frac{16}{11}\) = p
1 \(\frac{5}{11}\) = p
1 \(\frac{5}{11}\) = 1 \(\frac{5}{11}\) × 100% = 145 \(\frac{5}{11}\)%
32 bracelets are 145 \(\frac{5}{11}\)% of the number of bracelets that Emily produced. Anna produced 32 bracelets over the weekend, so Anna produced 145 \(\frac{5}{11}\)% of the number of bracelets that Emily produced.
Eureka Math Grade 7 Module 4 Lesson 3 Exercise Answer Key
Opening Exercise
If each 10 × 10 unit square represents one whole, then what percent is represented by the shaded region?
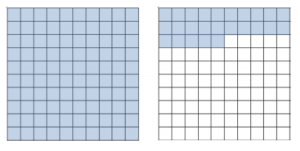
In the model above, 25% represents a quantity of 10 students. How many students does the shaded region represent?
Answer:
If 25% represents 10 students, then 1% represents \(\frac{10}{25}\), or \(\frac{2}{5}\), of a student. The shaded region covers 125 square units, or 125%, so since \(\frac{2}{5}\) ∙ 125 = 50, the shaded region represents 50 students.
Exercise 2.
There are 750 students in the seventh – grade class and 625 students in the eighth – grade class at Kent Middle School.
a. What percent is the seventh – grade class of the eighth – grade class at Kent Middle School?
The number of eighth graders is the whole amount. Let p represent the percent of seventh graders compared to eighth graders.
Quantity = Percent × Whole
Let p represent the unknown percent.
750 = p(625)
750(\(\frac{1}{625}\)) = p(625)(\(\frac{1}{625}\))
1.2 = p
1.2 = 120%
The number of seventh graders is 120% of the number of eighth graders.
There are 20% more seventh graders than eighth graders.
Alternate solution: There are 125 more seventh graders. 125 = p(625), p = 0.20. There are 20% more seventh graders than eighth graders.
b. The principal will have to increase the number of eighth – grade teachers next year if the seventh – grade enrollment exceeds 110% of the current eighth – grade enrollment. Will she need to increase the number of teachers? Explain your reasoning.
Answer:
The principal will have to increase the number of teachers next year. In part (a), we found out that the seventh grade enrollment was 120% of the number of eighth graders, which is greater than 110%.
Exercise 3.
At Kent Middle School, there are 104 students in the band and 80 students in the choir. What percent of the number of students in the choir is the number of students in the band?
Answer:
The number of students in the choir is the whole.
Quantity = Percent × Whole
Let p represent the unknown percent.
104 = p(80)
p = 1.3
1.3 = 130%
The number of students in the band is 130% of the number of students in the choir.
Exercise 4.
At Kent Middle School, breakfast costs $1.25 and lunch costs $3.75. What percent of the cost of lunch is the cost of breakfast?
Quantity = Percent × Whole
Let p represent the unknown percent.
1.25 = p(3.75)
1.25(\(\frac{1}{3.75}\)) = p(3.75)(\(\frac{1}{3.75}\))
p = \(\frac{1.25}{3.75}\)
p = \(\frac{1}{3}\)
\(\frac{1}{3}\) = \(\frac{1}{3}\) (100%) = 33 \(\frac{1}{3}\)%

The cost of breakfast is 33 \(\frac{1}{3}\)% of the cost of lunch.
Teacher may ask students what percent less than the cost of lunch is the cost of breakfast.
The cost of breakfast is 66\(\frac{2}{3}\)% less than the cost of lunch.
Teacher may ask what percent more is the cost of lunch than the cost of breakfast.
Let p represent the percent of lunch to breakfast.
3.75 = p(1.25)
3.75(\(\frac{1}{1.25}\)) = p(1.25)(\(\frac{1}{1.25}\))
p = \(\frac{3.75}{1.25}\) = 3 = 300%

The cost of lunch is 300% of the cost of breakfast.
Exercise 5.
Describe a real – world situation that could be modeled using the equation 398.4 = 0.83(x). Describe how the elements of the equation correspond with the real – world quantities in your problem. Then, solve your problem.
Answer:
Word problems will vary. Sample problem: A new tablet is on sale for 83% of its original sale price. The tablet is currently priced at $398.40. What was the original price of the tablet?
0.83 = \(\frac{83}{100}\) = 83%, so 0.83 represents the percent that corresponds with the current price. The current price ($398.40) is part of the original price; therefore, it is represented by 398.4. The original price is represented by x and is the whole quantity in this problem.
398.4 = 0.83x
\(\frac{1}{0.83}\) (398.4) = \(\frac{1}{0.83}\) (0.83)x
\(\frac{398.4}{0.83}\) = 1x
480 = x
The original price of the tablet was $480.00.
Eureka Math Grade 7 Module 4 Lesson 3 Problem Set Answer Key
Question 1.
Solve each problem using an equation.
a. 49.5 is what percent of 33?
Answer:
49.5 = p(33)
p = 1.5 = 150%
b. 72 is what percent of 180?
Answer:
72 = p(180)
p = 0.4 = 40%
c. What percent of 80 is 90?
Answer:
90 = p(80)
p = 1.125 = 112.5%
Question 2.
This year, Benny is 12 years old, and his mom is 48 years old.
a. What percent of his mom’s age is Benny’s age?
Answer:
Let p represent the percent of Benny’s age to his mom’s age.
12 = p(48)
p = 0.25 = 25%
Benny’s age is 25% of his mom’s age.
b. What percent of Benny’s age is his mom’s age?
Answer:
Let p represent the percent of his mom’s age to Benny’s age.
48 = p(12)
p = 4 = 400%
Benny’s mom’s age is 400% of Benny’s age.
c. In two years, what percent of his age will Benny’s mom’s age be at that time?
Answer:
In two years, Benny will be 14, and his mom will be 50.
14 → 100%
1 → (\(\frac{100}{14}\))%
50 → 50(\(\frac{100}{14}\)%
50 → 25(\(\frac{100}{7}\))%
50 → (\(\frac{2500}{7}\))%
50 → 357 \(\frac{1}{7}\)%
His mom’s age will be 357 \(\frac{1}{7}\)% of Benny’s age at that time.
d. In 10 years, what percent will Benny’s mom’s age be of his age?
Answer:
In 10 years, Benny will be 22 years old, and his mom will be 58 years old.
22 → 100%
1 → \(\frac{100}{22}\)%
58 → 58(\(\frac{100}{22}\))%
58 → 29(\(\frac{100}{11}\))%
58 → \(\frac{2900}{11}\)%
58 → 263 \(\frac{7}{11}\)%
In 10 years, Benny’s mom’s age will be 263 \(\frac{7}{11}\)% of Benny’s age at that time.
e. In how many years will Benny be 50% of his mom’s age?
Answer:
Benny will be 50% of his mom’s age when she is 200% of his age (or twice his age). Benny and his mom are always 36 years apart. When Benny is 36, his mom will be 72, and he will be 50% of her age. So, in 24 years, Benny will be 50% of his mom’s age.
d. As Benny and his mom get older, Benny thinks that the percent of difference between their ages will decrease as well. Do you agree or disagree? Explain your reasoning.
Answer:
Student responses will vary. Some students might argue that they are not getting closer since they are always 36 years apart. However, if you compare the percents, you can see that Benny‘s age is getting closer to 100% of his mom’s age, even though their ages are not getting any closer.
Question 3.
This year, Benny is 12 years old. His brother Lenny’s age is 175% of Benny’s age. How old is Lenny?
Answer:
Let L represent Lenny’s age. Benny’s age is the whole.
L = 1.75(12)
L = 21
Lenny is 21 years old.
Question 4.
When Benny’s sister Penny is 24, Benny’s age will be 125% of her age.
a. How old will Benny be then?
Answer:
Let b represent Benny’s age when Penny is 24.
b = 1.25(24)
b = 30
When Penny is 24, Benny will be 30.
b. If Benny is 12 years old now, how old is Penny now? Explain your reasoning.
Answer:
Penny is 6 years younger than Benny. If Benny is 12 now, then Penny is 6.
Question 5.
Benny’s age is currently 200% of his sister Jenny’s age. What percent of Benny’s age will Jenny’s age be in 4 years?
If Benny is 200% of Jenny’s age, then he is twice her age, and she is half of his age. Half of 12 is 6. Jenny is currently 6 years old. In 4 years, Answer:
Jenny will be 10 years old, and Benny will be 16 years old.
Quantity = Percent × Whole. Let p represent the unknown percent. Benny’s age is the whole.
10 = p(16)
p = \(\frac{10}{16}\)
p = \(\frac{5}{8}\)
p = 0.625 = 62.5%
In 4 years, Jenny will be 62.5% of Benny’s age.
Question 6.
At the animal shelter, there are 15 dogs, 12 cats, 3 snakes, and 5 parakeets.
a. What percent of the number of cats is the number of dogs?
Answer:
\(\frac{15}{12}\) = 1.25. That is 125%. The number of dogs is 125% the number of cats.
b. What percent of the number of cats is the number of snakes?
Answer:
\(\frac{3}{12}\) = \(\frac{1}{4}\) = 0.25. There are 25% as many snakes as cats.
c. What percent less parakeets are there than dogs?
Answer:
\(\frac{5}{15}\) = \(\frac{1}{3}\). That is 33 \(\frac{1}{3}\)%. There are 66 \(\frac{2}{3}\)% less parakeets than dogs.
d. Which animal has 80% of the number of another animal?
Answer:
\(\frac{12}{15}\) = \(\frac{4}{5}\) = \(\frac{8}{10}\) = 0.80. The number of cats is 80% the number of dogs.
e. Which animal makes up approximately 14% of the animals in the shelter?
Answer:
Quantity = Percent × Whole. The total number of animals is the whole.
q = 0.14(35)
q = 4.9
The quantity closest to 4.9 is 5, the number of parakeets.
Question 7.
Is 2 hours and 30 minutes more or less than 10% of a day? Explain your answer.
Answer:
2 hr.30 min. → 2.5 hr.; 24 hours is a whole day and represents the whole quantity in this problem.
10% of 24 hours is 2.4 hours.
2.5 > 2.4, so 2 hours and 30 minutes is more than 10% of a day.
Question 8.
A club’s membership increased from 25 to 30 members.
a. Express the new membership as a percent of the old membership.
Answer:
The old membership is the whole.
Quantity = Percent × Whole. Let p represent the unknown percent.
30 = p(25)
p = 1.2 = 120%
The new membership is 120% of the old membership.
b. Express the old membership as a percent of the new membership.
Answer:
The new membership is the whole.
30 → 100%
1 → \(\frac{100}{30}\)%
25 → 25 ∙ \(\frac{100}{30}\)%
25 → 5 ∙ 1\(\frac{100}{6}\)%
25 → \(\frac{500}{6}\)% = 83 \(\frac{1}{3}\)%
The old membership is 83 \(\frac{1}{3}\)% of the new membership.
Question 9.
The number of boys in a school is 120% the number of girls at the school.
a. Find the number of boys if there are 320 girls.
Answer:
The number of girls is the whole.
Quantity = Percent × Whole.
Let b represent the unknown number of boys at the school.
b = 1.2(320)
b = 384
If there are 320 girls, then there are 384 boys at the school.
b. Find the number of girls if there are 360 boys.
Answer:
The number of girls is still the whole.
Quantity = Percent × Whole.
Let g represent the unknown number of girls at the school.
360 = 1.2(g)
g = 300
If there are 360 boys at the school, then there are 300 girls.
Question 10.
The price of a bicycle was increased from $300 to $450.
a. What percent of the original price is the increased price?
Answer:
The original price is the whole.
Quantity = Percent × Whole. Let p represent the unknown percent.
450 = p(300)
p = 1.5
1.5 = \(\frac{150}{100}\) = 150%
The increased price is 150% of the original price.
b. What percent of the increased price is the original price?
Answer:
The increased price, $450, is the whole.
450 → 100%
1 → \(\frac{100}{450}\)%
300 → 300(\(\frac{100}{450}\))%
300 → 2(\(\frac{100}{3}\))%
300 → \(\frac{200}{3}\)%
300 → 66 \(\frac{2}{3}\)%
The original price is 66 \(\frac{2}{3}\)% of the increased price.
Question 11.
The population of Appleton is 175% of the population of Cherryton.
a. Find the population in Appleton if the population in Cherryton is 4,000 people.
Answer:
The population of Cherryton is the whole.
Quantity = Percent × Whole. Let a represent the unknown population of Appleton.
a = 1.75(4,000)
a = 7,000
If the population of Cherryton is 4,000 people, then the population of Appleton is 7,000 people.
b. Find the population in Cherryton if the population in Appleton is 10,500 people.
Answer:
The population of Cherryton is still the whole.
Quantity = Percent × Whole. Let c represent the unknown population of Cherryton.
10,500 = 1.75c
c = 10,500÷1.75
c = 6,000
If the population of Appleton is 10,500 people, then the population of Cherryton is 6,000 people.
Question 12.
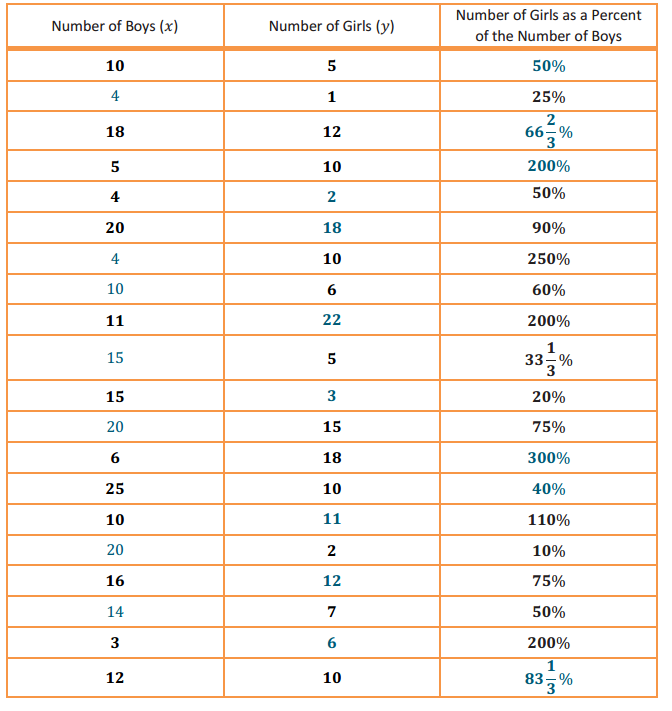
A statistics class collected data regarding the number of boys and the number of girls in each classroom at their school during homeroom. Some of their results are shown in the table below.
a. Complete the blank cells of the table using your knowledge about percent.
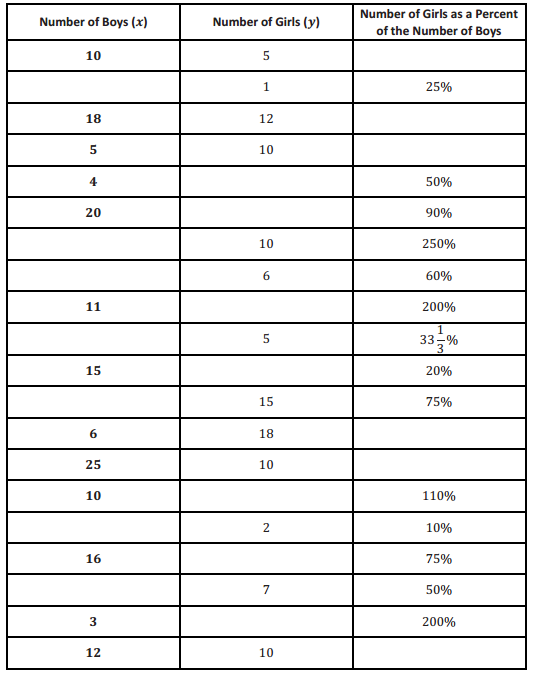
Answer:
b. Using a coordinate plane and grid paper, locate and label the points representing the ordered pairs (x,y).
Answer:
See graph to the right.
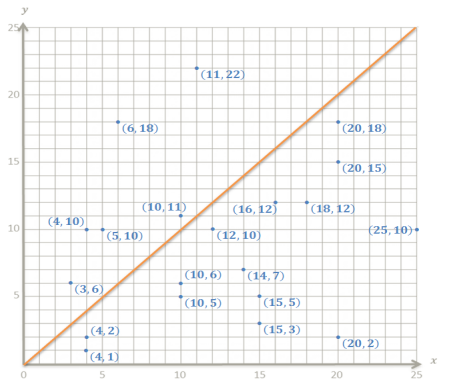
c. Locate all points on the graph that would represent classrooms in which the number of girls y is 100% of the number of boys x. Describe the pattern that these points make.
Answer:
The points lie on a line that includes the origin; therefore, it is a proportional relationship.
d. Which points represent the classrooms in which the number of girls as a percent of the number of boys is greater than 100%? Which points represent the classrooms in which the number of girls as a percent of the number of boys is less than 100%? Describe the locations of the points in relation to the points in part (c).
Answer:
All points where y > x are above the line and represent classrooms where the number of girls is greater than 100% of the number of boys. All points where y < x are below the line and represent classrooms where the number of girls is less than 100% of the boys.
e. Find three ordered pairs from your table representing classrooms where the number of girls is the same percent of the number of boys. Do these points represent a proportional relationship? Explain your reasoning.
Answer:
There are two sets of points that satisfy this question:
{(3,6), (5,10), and (11,22)}: The points do represent a proportional relationship because there is a constant of proportionality k = \(\frac{y}{x}\) = 2.
{(4,2), (10,5), and (14,7)}: The points do represent a proportional relationship because there is a constant of proportionality k = \(\frac{y}{x}\) = \(\frac{1}{2}\).
f. Show the relationship(s) from part (e) on the graph, and label them with the corresponding equation(s).
Answer:
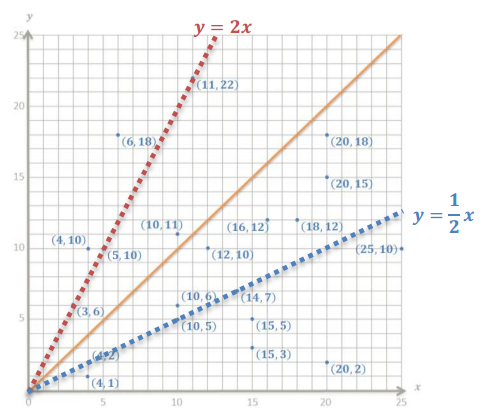
g. What is the constant of proportionality in your equation(s), and what does it tell us about the number of girls and the number of boys at each point on the graph that represents it? What does the constant of proportionality represent in the table in part (a)?
Answer:
In the equation y = 2x, the constant of proportionality is 2, and it tells us that the number of girls will be twice the number of boys, or 200% of the number of boys, as shown in the table in part (a).
In the equation y = 1/2 x, the constant of proportionality is 1/2, and it tells us that the number of girls will be half the number of boys, or 50% of the number of boys, as shown in the table in part (a).
Eureka Math Grade 7 Module 4 Lesson 3 Exit Ticket Answer Key
Solve each problem below using at least two different approaches.
Question 1.
Jenny’s great – grandmother is 90 years old. Jenny is 12 years old. What percent of Jenny’s great – grandmother’s age is Jenny’s age?
Answer:
Algebraic Solution:
Quantity = Percent × Whole. Let p represent the unknown percent.
Jenny’s great – grandmother’s age is the whole.
12 = p(90)
12 ∙ \(\frac{1}{90}\) = p(90) ∙ \(\frac{1}{90}\)
2 ∙ \(\frac{1}{15}\) = p(1)
\(\frac{2}{15}\) = p
\(\frac{2}{15}\) = \(\frac{2}{15}\) (100%) = 13 \(\frac{1}{3}\)%
Jenny’s age is 13 1/3% of her great – grandmother’s age.
Numeric Solution:
90 → 100%
1 → \(\frac{100}{90}\)%
12 → (12 ∙ \(\frac{100}{90}\))%
12 → (100 ∙ \(\frac{12}{90}\))%
12 → 100(\(\frac{2}{15}\))%
12 → 20(\(\frac{2}{3}\))%
12 → (\(\frac{40}{3}\))%
12 → 13 \(\frac{1}{3}\)%
Alternative Numeric Solution:
90 → 100%
9 → 10%
3 → \(\frac{10}{3}\)%
12 → 4(\(\frac{10}{3}\))%
12 → (\(\frac{40}{3}\))%
12 → 13 \(\frac{1}{3}\)%
Question 2.
Jenny’s mom is 36 years old. What percent of Jenny’s mother’s age is Jenny’s great – grandmother’s age?
Answer:
Quantity = Percent × Whole.
Let p represent the unknown percent. Jenny’s mother’s age is the whole.
90 = p(36)
90 ∙ \(\frac{1}{36}\) = p(36) ∙ \(\frac{1}{36}\)
5 ∙ \(\frac{1}{2}\) = p(1)
2.5 = p
2.5 = 250%
Jenny’s great grandmother’s age is 250% of Jenny’s mother’s age.
Eureka Math Grade 7 Module 4 Lesson 3 Part, Whole, or Percent—Round 1 Answer Key
Directions: Find each missing value.
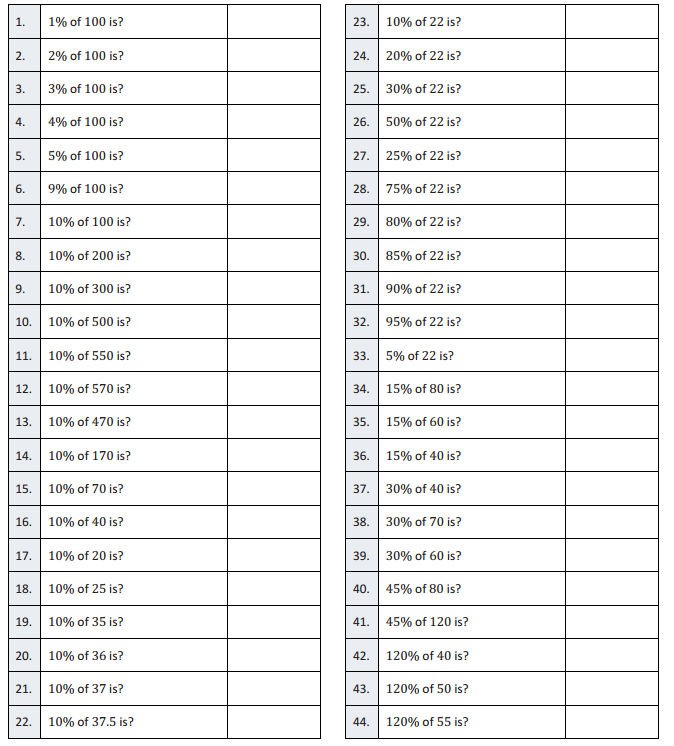
Answer:
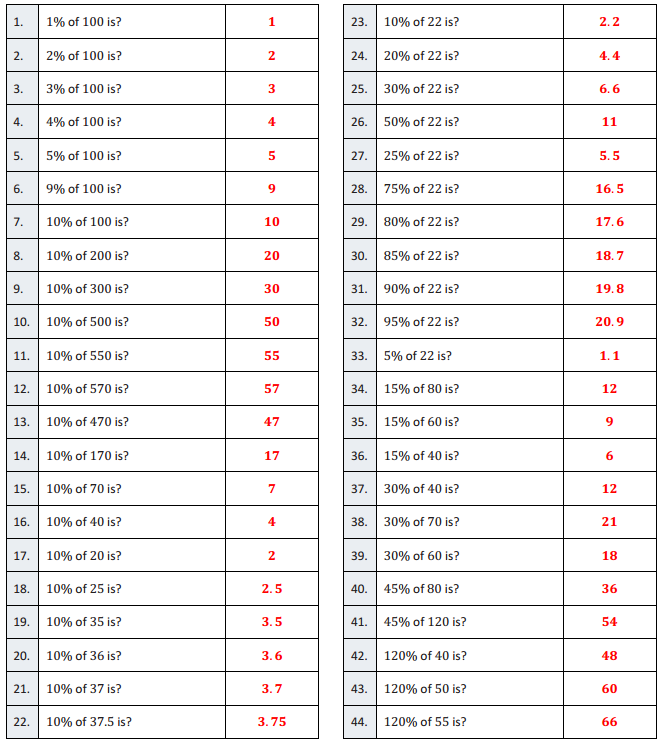
Eureka Math Grade 7 Module 4 Lesson 3 Part, Whole, or Percent—Round 2 Answer Key
Directions: Find each missing value.

Answer: