Engage NY Eureka Math 7th Grade Module 4 Lesson 11 Answer Key
Eureka Math Grade 7 Module 4 Lesson 11 Exercise Answer Key
Opening Exercise: Tax, Commission, Gratuity, and Fees
How are each of the following percent applications different, and how are they the same? Solve each problem, and then compare your solution process for each problem.
a. Silvio earns 10% for each car sale he makes while working at a used car dealership. If he sells a used car for $2,000, what is his commission?
Answer:
His commission is $200.
b. Tu’s family stayed at a hotel for 10 nights on their vacation. The hotel charged a 10% room tax, per night. How much did they pay in room taxes if the room cost $200 per night?
Answer:
They paid $200.
c. Eric bought a new computer and printer online. He had to pay 10% in shipping fees. The items totaled $2,000. How much did the shipping cost?
Answer:
The shipping cost $200.
d. Selena had her wedding rehearsal dinner at a restaurant. The restaurant’s policy is that gratuity is included in the bill for large parties. Her father said the food and service were exceptional, so he wanted to leave an extra 10% tip on the total amount of the bill. If the dinner bill totaled $2,000, how much money did her father leave as the extra tip?
Answer:
Her father left $200 as the extra tip.
For each problem, I had to find 10% of the total ($2,000). Even though each problem was different—one was a commission, one was a tax, one was a fee, and one was a gratuity—I arrived at the answer in the same manner, by taking 10% of $2,000 means \(\frac{1}{10}\) of $2,000, which is $200.
Exercises 1 – 4
Show all work; a calculator may be used for calculations.
The school board has approved the addition of a new sports team at your school.
Exercise 1.
The district ordered 30 team uniforms and received a bill for $2,992.50. The total included a 5% discount.
a. The school needs to place another order for two more uniforms. The company said the discount will not apply because the discount only applies to orders of $1,000 or more. How much will the two uniforms cost?
Answer:
Quantity = Percent∙Whole
2,992.50 = 0.95W
2,992.50(\(\frac{1}{0.95}\)) = 0.95(\(\frac{1}{0.95}\))W
3,150 = W
30 uniforms cost $3,150 before the discount. ($3,150)/30 per uniform means each uniform costs $105.
$105 × 2 = $210, so it will cost $210 for 2 uniforms without a discount.
b. The school district does not have to pay the 8% sales tax on the $2,992.50 purchase. Estimate the amount of sales tax the district saved on the $2,992.50 purchase. Explain how you arrived at your estimate.
Answer:
$2,992.50≈$3,000. To find 8% of $3,000, I know 8% of 100 is 8, since percent means per hundred. 8% of 1,000 is ten times as much since 1,000 is ten times as much as 100. 8(10) = 80. Then, I multiplied that by 3 since it is $3,000, so 3(80) = 240. The district saved about $240 in sales tax.
c. A student who loses a uniform must pay a fee equal to 75% of the school’s cost of the uniform. For a uniform that cost the school $105, will the student owe more or less than $75 for the lost uniform? Explain how to use mental math to determine the answer.
Answer:
75% means 75 per hundred. Since the uniform cost more than $100, a 75% fee will be more than $75.
d. Write an equation to represent the proportional relationship between the school’s cost of a uniform and the amount a student must pay for a lost uniform. Use u to represent the uniform cost and s to represent the amount a student must pay for a lost uniform. What is the constant of proportionality?
Answer:
s = 0.75u; the constant of proportionality is 75% = 0.75.
Exercise 2.
A taxpayer claims the new sports team caused his school taxes to increase by 2%.
a. Write an equation to show the relationship between the school taxes before and after a 2% increase. Use b to represent the dollar amount of school tax before the 2% increase and t to represent the dollar amount of school tax after the 2% increase.
Answer:
t = 1.02b
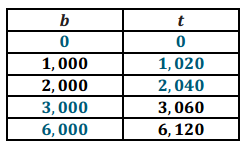
b. Use your equation to complete the table below, listing at least 5 pairs of values.
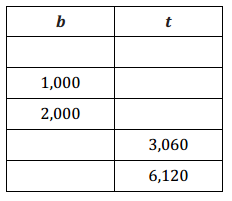
Answer:
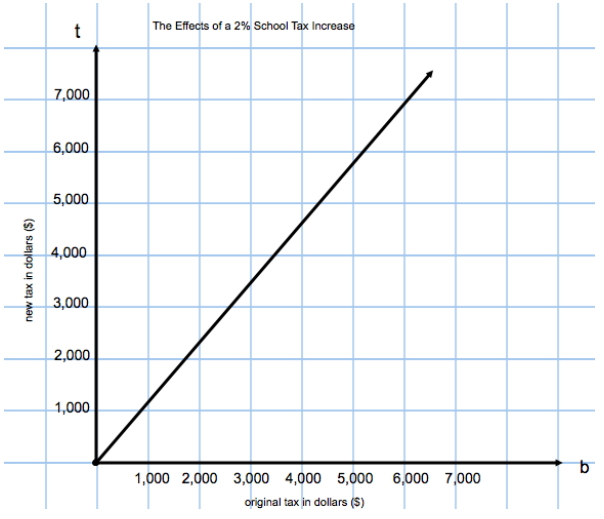
c. On graph paper, graph the relationship modeled by the equation in part (a). Be sure to label the axes and scale.
Answer:
d. Is the relationship proportional? Explain how you know.
Answer:
Yes. The graph is a straight line that touches the point (0,0).
e. What is the constant of proportionality? What does it mean in the context of the situation?
Answer:
The constant of proportionality is 1.02. It means that after the 2% tax increase, $1.02 will be paid for every dollar of tax paid before the increase.
f. If a taxpayers’ school taxes rose from $4,000 to $4,020, was there a 2% increase? Justify your answer using your graph, table, or equation.
Answer:
No. The change represents less than a 2% increase. On my graph, the point (4000,4020) does not fall on the line; it falls below the line, which means 4,020 is too low for the second coordinate (the new tax amount). If I examined my table, when b is 4,000, t is 4,080. The equation would be
4,000(1.02) = 4,080, which is not equivalent to 4,020.
Exercise 3.
The sports booster club is selling candles as a fundraiser to support the new team. The club earns a commission on its candle sales (which means it receives a certain percentage of the total dollar amount sold). If the club gets to keep 30% of the money from the candle sales, what would the club’s total sales have to be in order to make at least $500?
Answer:
Part = Percent∙Whole
500 = 0.3W
500(\(\frac{1}{0.3}\)) = 0.3(\(\frac{1}{0.3}\))W
1,666.67 ≈ W
They will need candle sales totaling at least $1,666.67.
Exercise 4.
Christian’s mom works at the concession stand during sporting events. She told him they buy candy bars for $0.75 each and mark them up 40% to sell at the concession stand. What is the amount of the markup? How much does the concession stand charge for each candy bar?
Answer:
Let N represent the new price of a candy after the markup. Let M represent the percent or markup rate.
N = M∙Whole
N = (100% + 40%)(0.75)
N = (1 + 0.4)(0.75)
N = 1.05
The candy bars cost $1.05 at the concession stand. $1.05 – $0.75 = $0.30, so there is a markup of $0.30.
With your group, brainstorm solutions to the problems below. Prepare a poster that shows your solutions and math work. A calculator may be used for calculations.
Exercise 5.
For the next school year, the new soccer team will need to come up with $600.
a. Suppose the team earns $500 from the fundraiser at the start of the current school year, and the money is placed for one calendar year in a savings account earning 0.5% simple interest annually. How much money will the team still need to raise to meet next year’s expenses?
Answer:
Interest = Principal × Interest Rate × Time
Interest = $500 × 0.005 × 1
Interest = $2.50
Total Money Saved = Interest + Principal = $500.00 + $2.50 = $502.50
Total Money Needed For Next Year = $600.00 – $502.50 = $97.50
The team will need to raise $97.50 more toward their goal.
b. Jeff is a member of the new sports team. His dad owns a bakery. To help raise money for the team, Jeff’s dad agrees to provide the team with cookies to sell at the concession stand for next year’s opening game. The team must pay back the bakery $0.25 for each cookie it sells. The concession stand usually sells about 60 to 80 baked goods per game. Using your answer from part (a), determine a percent markup for the cookies the team plans to sell at next year’s opening game. Justify your answer.
Answer:
The team needs to raise $97.50. Based on past data for the typical number of baked goods sold, we estimate that we will sell 60 cookies, so we need to divide 97.50 by 60. 97.5÷60 is about 1.63. That means we need to make a profit of $1.63 per cookie after we pay back the bakery $0.25 per cookie. So, if we add $0.25 to $1.63, we arrive at a markup price of $1.88. We decide to round that up to $2.00 since we want to be sure we raise enough money. We may sell fewer than 60 cookies (especially if the data for the typical number of baked goods sold includes items other than cookies, such as cupcakes or muffins).
To find the percent markup, we used the following equation with $0.25 as the original price; since
$2.00 – $0.25 = $1.75, then $1.75 is the markup.
Markup = Markup Rate∙Original Price
1.75 = Markup Rate∙(0.25)
1.75(\(\frac{1}{0.25}\)) = Markup Rate∙(0.25)(\(\frac{1}{0.25}\))
7 = Markup Rate
7 = \(\frac{7}{1}\) = \(\frac{700}{100}\) = 700% markup
c. Suppose the team ends up selling 78 cookies at next year’s opening game. Find the percent error in the number of cookies that you estimated would be sold in your solution to part (b).
Percent Error = \(\frac{|a – x|}{|x|}\) ∙100%, where x is the exact value and a is the approximate value.
Answer:
We estimated 60 cookies would be sold, but if 78 are sold, then 78 is the actual value. Next, we used the percent error formula:
Percent Error = \(\frac{|a – x|}{|x|}\)∙100%
Percent Error = \(\frac{|60 – 78|}{|78|}\)∙100%
Percent Error = \(\frac{18}{78}\)∙100%
Percent Error ≈ 23%
There was about a 23% error in our estimate for the number of cookies sold.
Eureka Math Grade 7 Module 4 Lesson 11 Problem Set Answer Key
Question 1.
A school district’s property tax rate rises from 2.5% to 2.7% to cover a $300,000 budget deficit (shortage of money). What is the value of the property in the school district to the nearest dollar? (Note: Property is assessed at 100% of its value.)
Answer:
Let W represent the worth of the property in the district, in dollars.
300,000 = 0.002W
300,000(\(\frac{1}{0.002}\)) = 0.002(\(\frac{1}{0.002}\))W
150,000,000 = W
The property is worth $150,000,000.
Question 2.
Jake’s older brother, Sam, has a choice of two summer jobs. He can either work at an electronics store or at the school’s bus garage. The electronics store would pay him to work 15 hours per week. He would make $8 per hour plus a 2% commission on his electronics sales. At the school’s bus garage, Sam could earn $300 per week working 15 hours cleaning buses. Sam wants to take the job that pays him the most. How much in electronics would Sam have to sell for the job at the electronics store to be the better choice for his summer job?
Answer:
Let S represent the amount, in dollars, sold in electronics.
300 < 8(15) + 0.02(S)
300 < 120 + 0.02S
180 < 0.02S
180(\(\frac{1}{0.02}\)) < 0.02(\(\frac{1}{0.05}\))S
9,000 < S
Sam would have to sell more than $9,000 in electronics for the electronics store to be the better choice.
Question 3.
Sarah lost her science book. Her school charges a lost book fee equal to 75% of the cost of the book. Sarah received a notice stating she owed the school $60 for the lost book.
a. Write an equation to represent the proportional relationship between the school’s cost for the book and the amount a student must pay for a lost book. Let B represent the school’s cost of the book in dollars and N represent the student’s cost in dollars.
Answer:
N = 0.75B
b. What is the constant or proportionality? What does it mean in the context of this situation?
Answer:
The constant of proportionality is 75% = 0.75. It means that for every $1 the school spends to purchase a textbook, a student must pay $0.75 for a lost book.
c. How much did the school pay for the book?
Answer:
60 = 0.75B
60(\(\frac{1}{0.75}\)) = 0.75(\(\frac{1}{0.75}\))B
\(\frac{60}{0.75}\) = B
80 = B
The school paid $80 for the science book.
Question 4.
In the month of May, a certain middle school has an average daily absentee rate of 8% each school day. The absentee rate is the percent of students who are absent from school each day.
a. Write an equation that shows the proportional relationship between the number of students enrolled in the middle school and the average number of students absent each day during the month of May. Let s represent the number of students enrolled in school, and let a represent the average number of students absent each day in May.
Answer:
a = 0.08s
b. Use your equation to complete the table. List 5 possible values for s and a.
Answer:
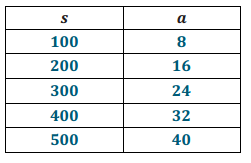
c. Identify the constant of proportionality, and explain what it means in the context of this situation.
Answer:
The constant of proportionality is 0.08. 0.08 = 8%, so on average, for every 100 students enrolled in school, 8 are absent from school.
d. Based on the absentee rate, determine the number of students absent on average from school during the month of May if there are 350 students enrolled in the middle school.
Answer:
28 students; 350 is halfway between 300 and 400. So, I used the table of values and looked at the numbers of students absent that correspond to 300 and 400 students at the school, which are 24 and 32. Halfway between 24 and 32 is 28.
Question 5.
The equation shown in the box below could relate to many different percent problems. Put an X next to each problem that could be represented by this equation. For any problem that does not match this equation, explain why it does not. Quantity = 1.05∙Whole
_________ Find the amount of an investment after 1 year with 0.5% interest paid annually.
Answer:
The equation should be Quantity = 1.005∙Whole.
________ Write an equation to show the amount paid for an item including tax, if the tax rate is 5%.
Answer:
X
________ A proportional relationship has a constant of proportionality equal to 105%.
X

Answer:

_______ Mr. Hendrickson sells cars and earns a 5% commission on every car he sells. Write an equation to show the relationship between the price of a car Mr. Hendrickson sold and the amount of commission he earns.
Answer:
The equation should be Quantity = 0.05∙Whole.
Eureka Math Grade 7 Module 4 Lesson 11 Exit Ticket Answer Key
Lee sells electronics. He earns a 5% commission on each sale he makes.
a. Write an equation that shows the proportional relationship between the dollar amount of electronics Lee sells, d, and the amount of money he makes in commission, c.
Answer:
c = \(\frac{1}{20}\)d or c = 0.05d
b. Express the constant of proportionality as a decimal.
Answer:
0.05
c. Explain what the constant of proportionality means in the context of this situation.
Answer:
The constant of proportionality of 0.05 means that Lee would earn five cents for every dollar of electronics that he sells.
d. If Lee wants to make $100 in commission, what is the dollar amount of electronics he must sell?
Answer:
c = 0.05 d
100 = 0.05 d
\(\frac{1}{0.05}\)(100) = \(\frac{1}{0.05}\)(0.05) d
2,000 = d
Lee must sell $2,000 worth of electronics.