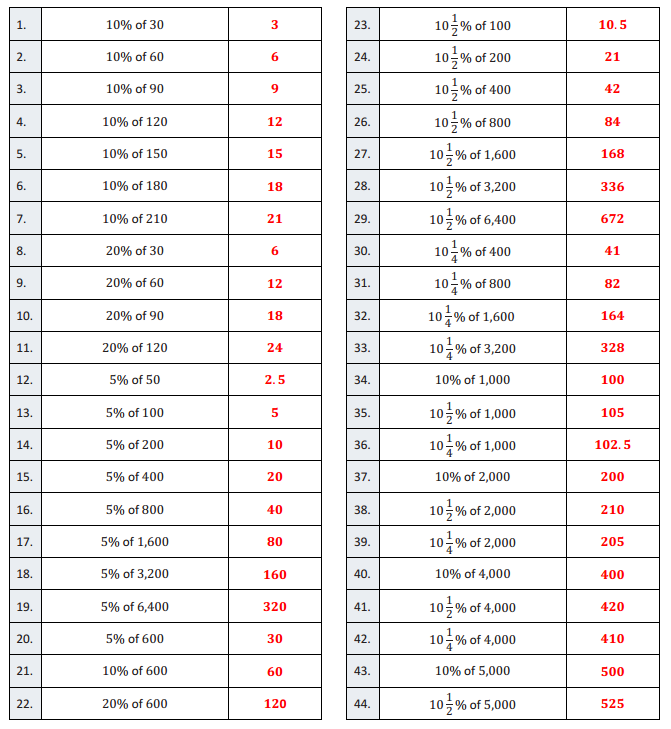
Engage NY Eureka Math 7th Grade Module 4 Lesson 10 Answer Key
Eureka Math Grade 7 Module 4 Lesson 10 Example Answer Key
Example 1: Can Money Grow? A Look at Simple Interest
Larry invests $100 in a savings plan. The plan pays 4 \(\frac{1}{2}\)% interest each year on his $100 account balance.
a. How much money will Larry earn in interest after 3 years? After 5 years?
Answer:
3 years:
I = Prt
I = 100(0.045)(3)
I = 13.50
Larry will earn $13.50 in interest after 3 years.
5 years:
I = Prt
I = 100(0.045)(5)
I = 22.50
Larry will earn $22.50 in interest after 5 years.
b. How can you find the balance of Larry’s account at the end of 5 years?
Answer:
You would add the interest earned after 5 years to the beginning balance. $22.50 + $100 = $122.50.
Example 2: Time Other Than One Year
A $1,000 savings bond earns simple interest at the rate of 3% each year. The interest is paid at the end of every month. How much interest will the bond have earned after 3 months?
Answer:
Step 1: Convert 3 months to a year.
12 months = 1 year. So, divide both sides by 4 to get 3 months = \(\frac{1}{4}\) year.
Step 2: Use the interest formula to find the answer.
I = Prt
I = ($1000)(0.03)(0.25)
I = $7.50
The interest earned after 3 months is $7.50.
Example 3: Solving for P, r, or t
Mrs. Williams wants to know how long it will take an investment of $450 to earn $200 in interest if the yearly interest rate is 6.5%, paid at the end of each year.
Answer:
I = Prt
$200 = ($450)(0.065)t
$200 = $29.25t
$200(1/($29.25)) = (1/($29.25))$29.25t
6.8376 = t
Six years is not enough time to earn $200. At the end of seven years, the interest will be over $200. It will take seven years since the interest is paid at the end of each year.
Eureka Math Grade 7 Module 4 Lesson 10 Exercise Answer Key
Exercise 1.
Find the balance of a savings account at the end of 10 years if the interest earned each year is 7.5%. The principal is $500.
Answer:
I = Prt
I = $500(0.075)(10)
I = $375
The interest earned after 10 years is $375. So, the balance at the end of 10 years is $375 + $500 = $875.
Exercise 2.
Write an equation to find the amount of simple interest, A, earned on a $600 investment after 1 1/2 years if the semi – annual (6 – month) interest rate is 2%.
Answer:
1 \(\frac{1}{2}\)years is the same as

Interest = Principal × Rate × Time
A = 600(0.02)(3) 1.5 years is 1 year and 6 months, so t = 3.
A = 36
The amount of interest earned is $36.
Exercise 3.
A $1,500 loan has an annual interest rate of 4 \(\frac{1}{4}\)% on the amount borrowed. How much time has elapsed if the interest is now $127.50?
Answer:
Interest = Principal × Rate × Time
Let t be time in years.
127.50 = (1,500)(0.0425)t
127.50 = 63.75t
(127.50)(\(\frac{1}{63.75}\)) = (\(\frac{1}{63.75}\))(63.75)t
2 = t
Two years have elapsed.
Eureka Math Grade 7 Module 4 Lesson 10 Problem Set Answer Key
Question 1.
Enrique takes out a student loan to pay for his college tuition this year. Find the interest on the loan if he borrowed $2,500 at an annual interest rate of 6% for 15 years.
Answer:
I = 2,500(0.06)(15)
I = 2,250
Enrique would have to pay $2,250 in interest.
Question 2.
Your family plans to start a small business in your neighborhood. Your father borrows $10,000 from the bank at an annual interest rate of 8% rate for 36 months. What is the amount of interest he will pay on this loan?
Answer:
I = 10,000(0.08)(3)
I = 2,400
He will pay $2,400 in interest.
Question 3.
Mr. Rodriguez invests $2,000 in a savings plan. The savings account pays an annual interest rate of 5.75% on the amount he put in at the end of each year.
a. How much will Mr. Rodriguez earn if he leaves his money in the savings plan for 10 years?
Answer:
I = 2,000(0.0575)(10)
I = 1,150
He will earn $1,150.
b. How much money will be in his savings plan at the end of 10 years?
Answer:
At the end of 10 years, he will have $3,150 because $2,000 + $1,150 = $3,150.
c. Create (and label) a graph in the coordinate plane to show the relationship between time and the amount of interest earned for 10 years. Is the relationship proportional? Why or why not? If so, what is the constant of proportionality?
Answer:
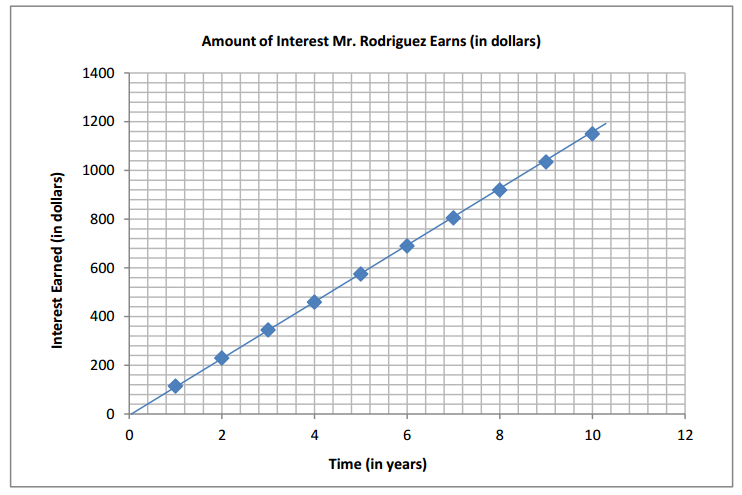
Yes, the relationship is proportional because the graph shows a straight line touching the origin. The constant of proportionality is 115 because the amount of interest earned increases by $115 for every one year.
d. Explain what the points (0,0) and (1,115) mean on the graph.
Answer:
(0, 0) means that no time has elapsed and no interest has been earned. (1, 115) means that after 1 year, the savings plan would have earned $115. 115 is also the constant of proportionality.
e. Using the graph, find the balance of the savings plan at the end of seven years.
Answer:
From the table, the point (7,805) means that the balance would be $2,000 + $805 = $2,805.
f. After how many years will Mr. Rodriguez have increased his original investment by more than 50%? Show your work to support your answer.
Answer:
Quantity = Percent × Whole
Let Q be the account balance that is 50% more than the original investment.
Q > (1 + 0.50)(2,000)
Q > 3,000
The balance will be greater than $3,000 beginning between 8 and 9 years because the graph shows (8, 920) and (9, 1035), so $2,000 + $920 = $2,920<$3,000, and $2,000 + $1,035 = $3,035 > $3,000.
Challenge Problem:
Question 4.
George went on a game show and won $60,000. He wanted to invest it and found two funds that he liked. Fund 250 earns 15% interest annually, and Fund 100 earns 8% interest annually. George does not want to earn more than $7,500 in interest income this year. He made the table below to show how he could invest the money.
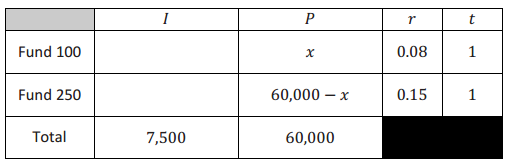
Answer:

a. Explain what value x is in this situation.
Answer:
x is the principal, in dollars, that George could invest in Fund 100.
b. Explain what the expression 60,000 – x represents in this situation.
Answer:
60,000 – x is the principal, in dollars, that George could invest in Fund 250. It is the money he would have left over once he invests in Fund 100.
c. Using the simple interest formula, complete the table for the amount of interest earned.
Answer:
See the table above.
d. Write an inequality to show the total amount of interest earned from both funds.
Answer:
0.08x + 0.15(60,000 – x)≤7,500
e. Use algebraic properties to solve for x and the principal, in dollars, George could invest in Fund 100. Show your work.
Answer:
0.08x + 9,000 – 0.15x ≤ 7,500
9,000 – 0.07x ≤ 7,500
9,000 – 9,000 – 0.07x ≤ 7,500 – 9,000
– 0.07x ≤ – 1,500
(\(\frac{1}{ – 0.07}\))( – 0.07x) ≤ (\(\frac{1}{ – 0.07}\))( – 1,500)
x ≥ 21,428.57
x approximately equals $21,428.57. George could invest $21,428.57 or more in Fund 100.
f. Use your answer from part (e) to determine how much George could invest in Fund 250.
Answer:
He could invest $38,571.43 or less in Fund 250 because 60,000 – 21,428.57 = 38,571.43.
g. Using your answers to parts (e) and (f), how much interest would George earn from each fund?
Answer:
Fund 100: 0.08 × 21,428.57 × 1 approximately equals $1,714.29.
Fund 250: 0.15 × 38,571.43 × 1 approximately equals $5,785.71 or $7,500 – $1,714.29.
Eureka Math Grade 7 Module 4 Lesson 10 Exit Ticket Answer Key
Question 1.
Erica’s parents gave her $500 for her high school graduation. She put the money into a savings account that earned 7.5% annual interest. She left the money in the account for nine months before she withdrew it. How much interest did the account earn if interest is paid monthly?
Answer:
I = Prt
I = (500)(0.075)(\(\frac{9}{12}\))
I = 28.125
The interest earned is $28.13.
Question 2.
If she would have left the money in the account for another nine months before withdrawing, how much interest would the account have earned?
Answer:
I = Prt
I = (500)(0.075)(\(\frac{18}{12}\))
I = 56.25
The account would have earned $56.25.
Question 3.
About how many years and months would she have to leave the money in the account if she wants to reach her goal of saving $750?
Answer:
750 – 500 = 250 She would need to earn $250 in interest.
I = Prt
250 = (500)(0.075)t
250 = 37.5t
250(\(\frac{1}{37.5}\)) = (\(\frac{1}{37.5}\))(37.5)t
6 \(\frac{2}{3}\) = t
It would take her 6 years and 8 months to reach her goal because \(\frac{2}{3}\) × 12 months is 8 months.
Eureka Math Grade 7 Module 4 Lesson 10 Fractional Percents—Round 1 Answer Key
Directions: Find the part that corresponds with each percent.
Answer:
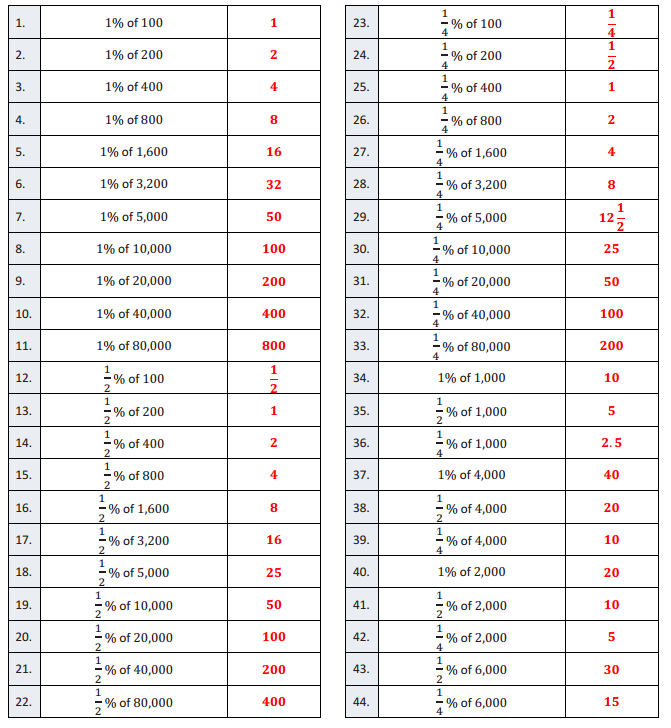
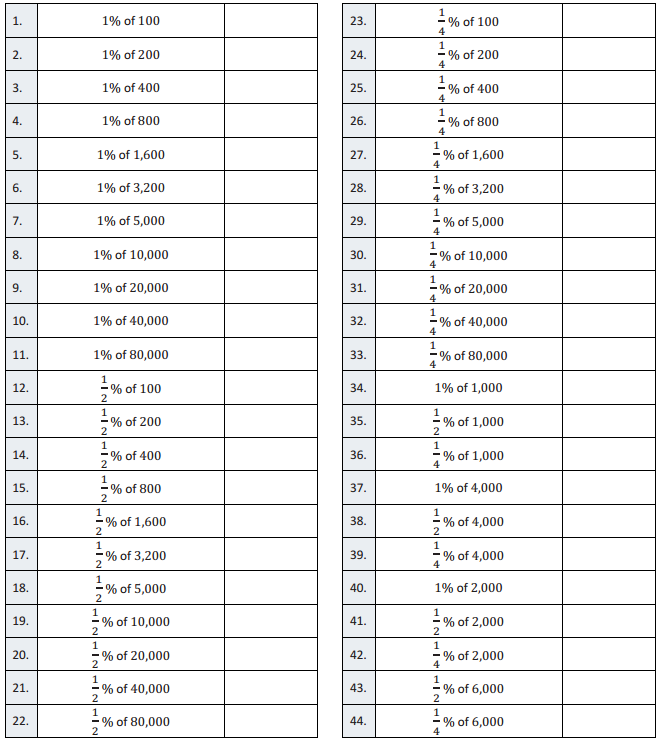
Eureka Math Grade 7 Module 4 Lesson 10 Fractional Percents—Round 2 Answer Key
Directions: Find the part that corresponds with each percent.
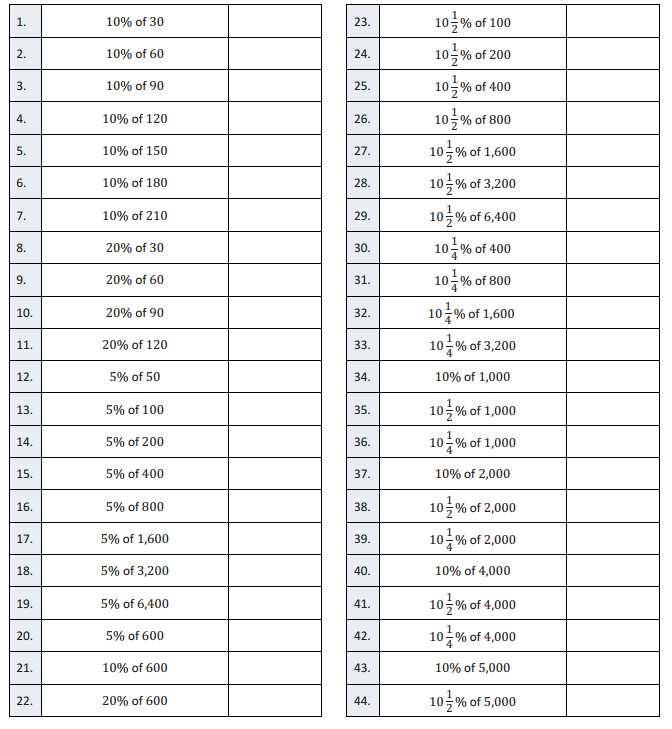
Answer: