Eureka Math Grade 7 Module 3 Lesson 24 Answer Key

Engage NY Eureka Math 7th Grade Module 3 Lesson 24 Answer Key

Eureka Math Grade 7 Module 3 Lesson 24 Exploratory Challenge Answer Key

Exploratory Challenge: Measuring a Container’s Capacity
A box in the shape of a right rectangular prism has a length of 12 in, a width of 6 in., and a height of 8 in. The base and the walls of the container are \(\frac{1}{4}\) in thick, and its top is open. What is the capacity of the right rectangular prism?
(Hint: The capacity is equal to the volume of water needed to fill the prism to the top.)

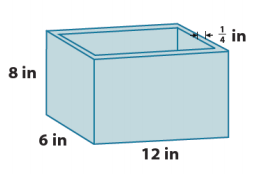
If the prism is filled with water, the water will take the shape of a right rectangular prism slightly smaller than the container. The dimensions of the smaller prism are a length of 11 \(\frac{1}{2}\) in, a width of 5 \(\frac{1}{2}\) in, and a height of 7 \(\frac{3}{4}\) in.
V = Bh
V = (lw)h
V = (11 \(\frac{1}{2}\) in ∙ 5 \(\frac{1}{2}\) in) ∙ 7 \(\frac{3}{4}\) in
V = (\(\frac{23}{2}\) in ∙ \(\frac{11}{2}\) in) ∙ \(\frac{31}{4}\) in
V = (25\(\frac{3}{4}\) in²) ∙ \(\frac{31}{4}\) in
V = \(\frac{7843}{16}\) in³
V = 490 \(\frac{3}{16}\) in³
The capacity of the right rectangular prism is 490 \(\frac{3}{16}\) in³.

Eureka Math Grade 7 Module 3 Lesson 24 Example Answer Key

Example 1: Measuring Liquid in a Container in Three Dimensions
A glass container is in the form of a right rectangular prism. The container is 10 cm long, 8 cm wide, and 30 cm high. The top of the container is open, and the base and walls of the container are 3 mm (or 0.3 cm) thick. The water in the container is 6 cm from the top of the container. What is the volume of the water in the container?

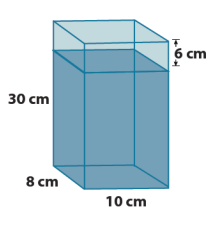
Answer:
Because of the walls and base of the container, the water in the container forms a right rectangular prism that is 9.4 cm long, 7.4 cm wide, and 23.7 cm tall.
V = Bh
V = (lw)h
V = (9.4 cm ∙ 7.4 cm) ∙ 23.7 cm
V = (\(\frac{94}{10}\) cm ∙ \(\frac{74}{10}\) cm) ∙ \(\frac{237}{10}\) cm
V = (\(\frac{6,956}{100}\) cm² ) ∙ \(\frac{237}{10}\) cm
V = \(\frac{1,648,572}{1,000}\) cm³
V = 1,648.572 cm³
The volume of the water in the container is 1,648.6 cm³.

Example 2.
7.2 L of water are poured into a container in the shape of a right rectangular prism. The inside of the container is 50 cm long, 20 cm wide, and 25 cm tall. How far from the top of the container is the surface of the water? (1 L = 1,000 cm³)

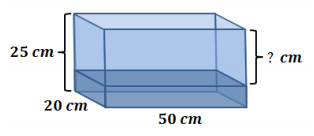
Answer:
7.2 L = 7,200 cm³
V = Bh
V = (lw)h
7,200 cm³ = (50 cm)(20 cm)h
7,200 cm³ = 1,000 cm² ∙ h
7,200 cm³ ∙ \(\frac{1}{1,000 \mathrm{~cm}^{2}}\) = 1,000 cm² ∙ \(\frac{1}{1,000 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{7,200}{1,000}\) cm = 1 ∙ h
7.2 cm = h
The depth of the water is 7.2 cm. The height of the container is 25 cm.
25 cm – 7.2 cm = 17.8 cm
The surface of the water is 17.8 cm from the top of the container.

Example 3.
A fuel tank is the shape of a right rectangular prism and has 27 L of fuel in it. It is determined that the tank is \(\frac{3}{4}\) full. The inside dimensions of the base of the tank are 90 cm by 50 cm. What is the height of the fuel in the tank? How deep is the tank? (1 L = 1,000 cm³)
Answer:
Let the height of the fuel in the tank be h cm.
27 L = 27,000 cm³
V = Bh
V = (lw)h
27,000 cm³ = (90 cm ∙ 50 cm) ∙ h
27,000 cm³ = (4,500 cm² ) ∙ h
27,000 cm³ ∙ \(\frac{1}{4,500 \mathrm{~cm}^{2}}\) = 4,500 cm² ∙ \(\frac{1}{4,500 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{27,000}{4,500}\) cm = 1 ∙ h
6 cm = h
The height of the fuel in the tank is 6 cm. The height of the fuel is \(\frac{3}{4}\) the depth of the tank. Let d represent the depth of the tank in centimeters.
6 cm = \(\frac{3}{4}\) d
6 cm ∙ \(\frac{4}{3}\) = \(\frac{3}{4}\) ∙ \(\frac{4}{3}\) ∙ d
8 cm = d
The depth of the fuel tank is 8 cm.

Eureka Math Grade 7 Module 3 Lesson 24 Problem Set Answer Key

Question 1.
Mark wants to put some fish and decorative rocks in his new glass fish tank. He measured the outside dimensions of the right rectangular prism and recorded a length of 55 cm, width of 42 cm, and height of 38 cm. He calculates that the tank will hold 87.78 L of water. Why is Mark’s calculation of volume incorrect? What is the correct volume? Mark also failed to take into account the fish and decorative rocks he plans to add. How will this affect the volume of water in the tank? Explain.
Answer:
V = Bh = (lw)h
V = 55 cm ∙ 42 cm ∙ 38 cm
V = 2,310 cm² ∙ 38 cm
V = 87,780 cm³
87,780 cm³ = 87.78 L
Mark measured only the outside dimensions of the fish tank and did not account for the thickness of the sides of the tank. If he fills the tank with 87.78 L of water, the water will overflow the sides. Mark also plans to put fish and rocks in the tank, which will force water out of the tank if it is filled to capacity.

Question 2.
Leondra bought an aquarium that is a right rectangular prism. The inside dimensions of the aquarium are 90 cm long, by 48 cm wide, by 60 cm deep. She plans to put water in the aquarium before purchasing any pet fish. How many liters of water does she need to put in the aquarium so that the water level is 5 cm below the top?
Answer:
If the aquarium is 60 cm deep, then she wants the water to be 55 cm deep. Water takes on the shape of its container, so the water will form a right rectangular prism with a length of 90 cm, a width of 48 cm, and a height of 55 cm.
V = Bh = (lw)h
V = (90 cm ∙ 48 cm) ∙ 55 cm
V = 4,320 cm² ∙ 55 cm
V = 237,600 cm³
237,600 cm³ = 237.6 L
The volume of water needed is 237.6 L.

Question 3.
The inside space of two different water tanks are shown below. Which tank has a greater capacity? Justify your answer.

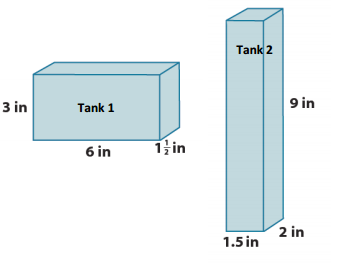
Answer:
V₁ = Bh = (lw)h
V₁ = (6 in. ∙ 1 \(\frac{1}{2}\) in.) ∙ 3 in.
V₁ = (6
V₁ = 9 in² ∙ 3 in.
V₁ = 27 in³

V₂ = Bh = (lw)h
V₂ = (1 \(\frac{1}{2}\) in. ∙ 2 in.) ∙ 9 in.
V₂ = (2 in² ÷ 1 in²) ∙ 9 in .
V₂ = 3 in² ∙ 9 in.
V₂ = 27 in³
The tanks have the same volume, 27 in³. Each prism has a face with an area of 18 in²(base) and a height that is 1 \(\frac{1}{2}\) in.

Question 4.
The inside of a tank is in the shape of a right rectangular prism. The base of that prism is 85 cm by 64 cm. What is the minimum height inside the tank if the volume of the liquid in the tank is 92 L ?
Answer:
V = Bh = (lw)h
92,000 cm³ = (85 cm ∙ 64 cm) ∙ h
92,000 cm³ = 5,440 cm² ∙ h
92,000 cm³ ∙ \(\frac{1}{5,440 \mathrm{~cm}^{2}}\) = 5,440 cm² ∙ \(\frac{1}{5,440 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{92,000}{5,440}\) cm = 1 ∙ h
16 \(\frac{31}{34}\) cm = h
The minimum height of the inside of the tank is 16 \(\frac{31}{34}\) cm.

Question 5.
An oil tank is the shape of a right rectangular prism. The inside of the tank is 36.5 cm long, 52 cm wide, and 29 cm high. If 45 liters of oil have been removed from the tank since it was full, what is the current depth of oil left in the tank?
Answer:
V = Bh = (lw)h
V = (36.5 cm ∙ 52 cm) ∙ 29 cm
V = 1,898 cm² ∙ 29 cm
V = 55,042 cm³
The tank has a capacity of 55,042 cm³, or 55.042 L.
55.042 L – 45 L = 10.042 L

If 45 L of oil have been removed from the tank, then 10.042 L are left in the tank.
V = Bh = (lw)h
10,042 cm³ = (36.5 cm ∙ 52 cm) ∙ h
10,042 cm³ = 1,898 cm² ∙ h
10,042 cm³ ∙ \(\frac{1}{1,898 \mathrm{~cm}^{2}}\) = 1,898 cm² ∙ \(\frac{1}{1,898 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{10,042}{1,898}\) cm = 1 ∙ h
5.29 cm ≈ h
The depth of oil left in the tank is approximately 5.29 cm.

Question 6.
The inside of a right rectangular prism – shaped tank has a base that is 14 cm by 24 cm and a height of 60 cm. The tank is filled to its capacity with water, and then 10.92 L of water is removed. How far did the water level drop?
Answer:
V = Bh = (lw)h
V = (14 cm ∙ 24 cm) ∙ 60 cm
V = 336 cm² ∙ 60 cm
V = 20,160 cm³
The capacity of the tank is 20,160 cm³ or 20.16 L.
20,160 cm³ – 10,920 cm³ = 9,240 cm³
When 10.92 L or 10,920 cm³ of water is removed from the tank, there remains 9,240 cm³ of water in the tank.

V = Bh = (lw)h
9,240 cm³ = (14 cm ∙ 24 cm) ∙ h
9,240 cm³ = 336 cm² ∙ h
9,240 cm³ ∙ \(\frac{1}{336 \mathrm{~cm}^{2}}\) = 336 cm² ∙ \(\frac{1}{336 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{9,240}{336}\) cm = 1 ∙ h
27 \(\frac{1}{2}\) cm = h
The depth of the water left in the tank is 27 \(\frac{1}{2}\) cm.
60 cm – 27 \(\frac{1}{2}\) cm = 32 \(\frac{1}{2}\) cm
This means that the water level has dropped 32 \(\frac{1}{2}\) cm.

Question 7.
A right rectangular prism – shaped container has inside dimensions of 7 \(\frac{1}{2}\) cm long and 4 \(\frac{3}{5}\) cm wide. The tank is \(\frac{3}{5}\) full of vegetable oil. It contains 0.414 L of oil. Find the height of the container.
Answer:
V = Bh = (lw)h
414 cm³ = (7 \(\frac{1}{2}\) cm ∙ 4 \(\frac{3}{5}\) cm) ∙ h
414 cm³ = 34 \(\frac{1}{2}\) cm² ∙ h
414 cm³ = \(\frac{69}{2}\) cm² ∙ h
414 cm³ ∙ \(\frac{2}{69 \mathrm{~cm}^{2}}\) = \(\frac{69}{2}\) cm² ∙ \(\frac{2}{69 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{828}{69}\) cm = 1 ∙ h
12 cm = h
The vegetable oil in the container is 12 cm deep, but this is only \(\frac{3}{5}\) of the container’s depth. Let d represent the depth of the container in centimeters.
12 cm = \(\frac{3}{5}\) ∙ d
12 cm ∙ \(\frac{5}{3}\) = \(\frac{3}{5}\) ∙ \(\frac{5}{3}\) ∙ d
\(\frac{60}{3}\) cm = 1 ∙ d
20 cm = d
The depth of the container is 20 cm.

Question 8.
A right rectangular prism with length of 10 in, width of 16 in, and height of 12 in is \(\frac{2}{3}\) filled with water. If the water is emptied into another right rectangular prism with a length of 12 in, a width of 12 in, and height of 9 in, will the second container hold all of the water? Explain why or why not. Determine how far (above or below) the water level would be from the top of the container.
Answer:
\(\frac{2}{3}\) ∙ 12 in = \(\frac{24}{3}\) in = 8 in The height of the water in the first prism is 8 in.
V = Bh = (lw)h
V = (10 in ∙ 16 in) ∙ 8 in
V = 160 in² ∙ 8 in
V = 1,280 in³
The volume of water is 1,280 in³.

V = Bh = (lw)h
V = (12 in ∙ 12 in) ∙ 9 in
V = 144 in² ∙ 9 in
V = 1,296 in³
The capacity of the second prism is 1,296 in³, which is greater than the volume of water, so the water will fit in the second prism.

V = Bh = (lw)h Let h represent the depth of the water in the second prism in inches.
1,280 in³ = (12 in ∙ 12 in) ∙ h
1,280 in³ = (144 in² ) ∙ h
1,280 in³ ∙ \(\frac{1}{144 \mathrm{in}^{2}}\) = 144 in² ∙ \(\frac{1}{144 \mathrm{in}^{2}}\) ∙ h
\(\frac{1,280}{144}\) in = 1 ∙ h
8 \(\frac{128}{144}\) in = h
8 \(\frac{8}{9}\) in = h
The depth of the water in the second prism is 8 \(\frac{8}{9}\) in.
9 in – 8 \(\frac{8}{9}\) in = \(\frac{1}{9}\) in
The water level will be \(\frac{1}{9}\) in from the top of the second prism.

Eureka Math Grade 7 Module 3 Lesson 24 Exit Ticket Answer Key

Lawrence poured 27.328 L of water into a right rectangular prism – shaped tank. The base of the tank is 40 cm by 28 cm. When he finished pouring the water, the tank was \(\frac{2}{3}\) full. (1 L = 1,000 cm³)
a. How deep is the water in the tank?
Answer:
27.328 L = 27,328 cm³
V = Bh
V = (lw)h
27,328 cm³ = (40 cm ∙ 28 cm) ∙ h
27,328 cm³ = 1,120 cm² ∙ h
27,328 cm³ ∙ \(\frac{1}{1,120 \mathrm{~cm}^{2}}\) = 1,120 cm² ∙ \(\frac{1}{1,120 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{27,328}{1,120}\) cm = 1 ∙ h
24\(\frac{280}{1,120}\) cm = h
24 \(\frac{2}{5}\) cm = h
The depth of the water is 24 \(\frac{2}{5}\) cm.

b. How deep is the tank?
Answer:
The depth of the water is \(\frac{2}{3}\) the depth of the tank. Let d represent the depth of the tank in centimeters.
24 \(\frac{2}{5}\) cm = \(\frac{2}{3}\) ∙ d
24 \(\frac{2}{5}\) cm ∙ \(\frac{3}{2}\) = \(\frac{2}{3}\) ∙ \(\frac{3}{2}\) ∙ d
36 cm ÷ \(\frac{3}{5}\) cm = 1d
36 \(\frac{3}{5}\) cm = d
The depth of the tank is 36 \(\frac{3}{5}\) cm.

c. How many liters of water can the tank hold in total?
Answer:
V = Bh
V = (lw)h
V = (40 cm ∙ 28 cm) ∙ 36 \(\frac{3}{5}\) cm
V = 1,120 cm² ∙ 36 \(\frac{3}{5}\) cm
V = 40,320 cm³ ÷ 672 cm³
V = 40,992 cm³
40,992 cm³ = 40.992 L The tank can hold up to 41.0 L of water.